359 2

359

8.5. Równania różnicowe

powód. Wielomian P stopnia m — 1 możemy wyrazić w postaci %(j)=t}₀+bj+b₂j(j-l)+    j(j-l)...(j-m+2).

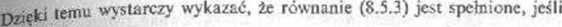
(p = l_s 2,.... w-1),

tzn jeśli jest równe wartości u^pd^p-uⁱfełu^p dla H=a_I( Podstawmy ją do lewej strony (8.5.3):

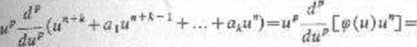
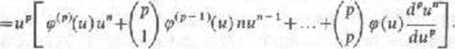
Ostatnie przekształcenie opiera się na worze Leibniza.

Wartości wielomianu ę i jego wszystkich pochodnych występujących w tym wyrażeniu są dla u-ui równe zeru, gdyż u_: jest sn-krotnym zerem tego wielomianu. Dlatego ciąg {yj określony w (8.5.6) spełnia równanie różnicowe.

Sumując rozwiązania lej postaci związane z różnymi pierwiastkami równania charakterystycznego, otrzymujemy rozwiązanie i k parametrami. Można wykazać (zob. Henrici {i 10], str. 214), że jego poszczególne składniki są niezależne liniowo. Dlatego powyższe twierdzenie jest już udowodnione,

Przykład 8.5.4. Równanie różnicowe: y_{lH 3} —3>.,_₂ 4 4y„-(J.

Równanie charakterystyczne: w³—3iz^ł + 4=0, pierwiastki: Wj = -1, u₂~u₃^2.

Rozwiązanie ogólne: y_fl=c, (— 1)^r+(c₂ + c_zn) • 2".

8.5.2. Dowolne liniowe równania różnicowe

Dowolny niejednorodny układ liniowy równań różnicowych rzędu pierwszego można napisać w postaci wektorowo-macierzowej:

gdzie U„} jest znanym ciągiem wektorów. Jeśli jest dana wartość początkowa y₀, to przez indukcję otrzymuje się, że

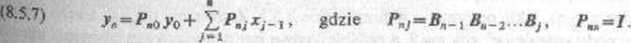
W szczególności, jeśli wszystkie B_a są równe B, to

n

(8.5.8)

y»=*yo+ Z^B” ^j*j-l-

J«*l

8.5.5. Równanie różnicowe: y_a+i-2y_n=(f. Warunek początkowy: y₀ = l ■