340 2

340

$. Równania różniczkowe

lub - ogólniej — metoda opisana równością

(8.3.12)

Istnieją modyfikacje ułatwiające zmianę długości kroku. Gdy k zwiększa się, obniża <T błąd lokalny obcięcia, ale pogarsza się stabihncść. I tutaj, jak i dla metedy trapezów trzef ba użyć metedy Newtona lub podobnej do niej.

8.3.6. Sterowanie długością kroku

początkowych. Oprócz obliczenia y i / trzeba w każdym kroku wykonać trzy czynności:

Utrzymywanie stałej długości kroku zazwyczaj nie jest ekonomiczne. Sterowanie automatyczne tą długością jest więc ważnym i ciekawym elementem programowania zagadnień

I. Oszacować błąd lokalny.

II.    Ustalić, czy można zaakceptować obliczoną wartość y, czy też należy cofnąć się do poprzedniego punktu i przyjąć krótszy kTok.

III.    Wyznaczyć długość kroku, której należy użyć.

Jeśli rząd dokładności metody jest równy p_y tzn. jeśli błąd globalny wynosi 0(k*), to błąd lokalny w x_H+i jest równy w przybliżeniu c_nłt*'^rl. Dla metod Rungego-Kutty c. zależy od pewnych pochodnych cząstkowych funkcji f których się nie oblicza. Zakładamy, że c_m zmienia się nieznacznie przy przejściu do następnego kroku.

Opiszemy teraz pewne sposoby szacowania błędu lokalnego. Startując z punktu (x_tt, .yj wykonujemy najpierw jeden krok o długości h. Wynik oznaczmy Cx«_{+ J}, y*+1). Następnie, startując znów z (*., y„), wykonujemy dwa kolejne kroki, każdy o długości \h. Ostateczny wynik oznaczmy (x_{n +},, y*+1). Zgodnie z (7.2.9) błąd lokalny można w przybliżeniu oszacować z góry za pomocą liczby

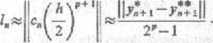
(8.3.13)

Wartość otrzymana za pomocą ekstrapolacji Richardsona (czynnej lub biernej zob. § 8.2), tj. taka, że

wydaje się lepszym niż y*t _x przybliżeniem wartości i)> ale nie jest łatwo na podstawie

Hortw»h /■»«■?!»*'/Yll/iJ/⁴ hlarł ćri^lci nił w ffł V

(8.3.14)

!«*źe(x,,₊ !-.<*).