414 (4)

--I

przy czym

P~' O

-'i

-1

Px

O

Wobec takiego uproszczenia, rozwiązanie (9.18) można przedstawić w postaci

o p-

d v

^d'^Y| j = -Px^!B^ri^_,Af PL = -

^dX_z j

p*Qn"

p-I X,	•1	Qi i
0	^P*»J	.0(2.

H^_l A? PL =

(9.22)

Px'<tf2

E“ Aj PL = -App^L

rdzie

3 = BPi'B⁷'=Q,₍p-^|Q_ll+Q_l2P^Qi^rj

(uzyskaną powyżej uogólnioną odwrotność A^p porównaj ze wzorem (1.39) 7. rozdz. 1.4). Jednak najczęściej przyjmuje się, ze Px Wówczas

pp_x

(9.23)

(Al sAp). Uogólniona odwrotność

i l_r

^Arr_x = Px B^TS“‘A?> - B^rE“‘A[P =

Ql!

Qn]

E"¹ A f P = A j>

o macierzy

E = BPx^!B^r =■ BB⁷ = QnQn + Qi2Q?2 jest g-dwrotnością Helmerta-Wolfa (zob. także rozdz. 1.4). Przyjmując dalsze uproszczenie P = l_n, uzyskujemy

(9.24)

iy ~^_App_xL —-ApL =-A ^fL

*dzie

A⁺ =

^Qi 1	__) . T n	aT Ai 1
	z. Aj P -	> - > L_

^A'^A| (A[A,A?'A, + A[ A₂A₂ A|) ' A^P A ■> A i i

jest odwrotnością Moorea'Penrose’a (A,^h sA⁺).

¹ r

9.3. Macierz kowariancji wyrównanych parametrów

Po swobodnym wyrównaniu sieci geodezyjnej zachodzi często konieczność przeprowadzenia analizy dokładności, obejmującej m.in.: wyznaczenie błędów średnich wyrównanych współrzędnych, błędów położenia lub elips ufności wszystkich punktów sieci. Związane z tym procedury obliczeniowe są bardzo podobne do tych, jakie stosuje się w rozwiązaniach klasycznych. Ustalenia wymaga jednak tutaj macierz kowariancji estymatora X - X° fd _Y , a tym samym macierz kowariancji wyrównanych współrzędnych wszystkich punktów swobodnej, geometrycznej struktui-y pomiarowej.

Ustalenie macierzy kowariancji bez uwzględnienia błędności wektora X°

Biorąc pod uwagę, że

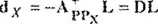
(D = -Ap_p ), oraz stosując zasadę propagacji macierzy kowariancji, uzyskujemy

Podstawiając Ap_{> =    P, macierz kowariancji estymatora

przyrostów bez uwzględnienia błędności wektora X° można zapisać w postaci

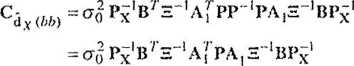
(9.25)

Ponieważ

X = X°+d*

gdzie X° nie jest wektorem losowym, więc także

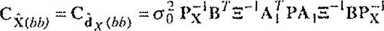
(9.26)

(przypomnijmy: E~BP_X¹B⁷ )•

415