52 (138)

Ot-:

I I i

3.1.5. Układy równań liniowych (I stopnia a O V ft#0) i dwiema niewiadomymi

n) l\»stnć układu równań liniowych z dwiema niewiadomymi .v i y to koniunkcja następujących równań: a, .v + b, y = f, A a,.v + b₂y = c₂, którą zapisujemy:

(a, .v + ł»,y = C, (każde z równań jest równaniem a, x + b, y = i', liniowym z dwiema niewiadomymi) b) Rozwiązać układ to obliczyć niewiadome x i y. c) Rozwiązaniem układu jest para liczb (.v; y) spełniających oba równania równocześnie, d) Metody rozwiązywania układu równań liniowych to metoda graficzna (rysunkowa) oraz kilka metod algebraicznych (rachunkowych), i e) Graficzna metoda rozwiązywania układów równań liniowych polega na graficznym zilustrowaniu każdego równania na płaszczyźnie z układem współrzędnych:

g) Metoda podstawiania polega na podstawianiu obliczonej z któregoś równania jednej niewiado-mej (x lub y) do innego równania, i otrzymania zeń równania z jedną niewiadomą. Po obliczeniu tej niewiadomej (znów podstawiając) obliczamy drugą niewiadomą, na przykład: c, b

^x ~ ~n~ ~ TT y

[ ^a\^x + b\ y = c_x

+ b₂y = c₂

x = -r,—

y =

Ja,.v + b_ly = c,

| a₂ x + b₂ y = Cj

Na przykład:

a, c,

y=-ir^x+ 7T^;b\^ ⁰

b„

#0

iijjjl

^bl(^a.^C2^_a2^C.)

y = C,

^ai(^ai^2 ^1 ^a2 przy stosownych zało-^ai^c2~ ^a2^ci    żeniach.

CO

O

",    c,

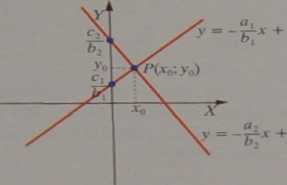
y=~t:^{x +} —''^b'

57

Gdy równania przedstawiają proste przecinające się w punkcie P(x₀;y₀), rozwiązaniem układu (w tym przykładzie) jest para liczb ( x₀; y_Q), czyli

współrzędne punktu przecięcia się prostych a. c, .    a, c₂

o równaniach: y =—-t— x + -g- i y =--g- x + -jj-

(dla b, # 0 #

Uwaga: Dwie proste na płaszczyźnie mogą albo przecinać się w jednym punkcie, albo być równoległe (rozłączne lub pokrywające się) — por. 3.1.6. Metoda graficzna jest dość szybka (wystarczy narysować dwie proste i zinterpretować ich wzajemne położenie na płaszczyźnie), lecz dokładne odczytanie współrzędnych punktu wspólnego może być trudne lub obarczone błędem, stąd warto ponadto stosować metody algebraiczne, f) Algebraiczne metody rozwiązywania układów równań liniowych polegają na rachunkowym obliczeniu liczb x i y spełniających układ równań. Poniżej są omówione trzy metody algebraiczne: metoda podstawiania, metoda przeciwnych współczynników oraz metoda wyznaczników.

^a,b₂-b,a₂ h) Metoda przeciwnych współczynników (inaczej — dodawania stronami) polega na uzyskaniu przeciwnych współczynników przy tej samej niewiadomej w obu równaniach i następnie na do-daniu obu równań stronami. Stąd obliczymy ko- \ lejne niewiadome: x oraz y, na przykład:

|a,x + b,y = c₁ ||

\a₂x + b₂y = c₂

1a_la₂x + b_xa₂y - c_ta₂    f dodajemy)

-a, a₂x - a, b₂y=-a_l c₂ [ stronami j, stąd (b, a₂-a_lb₃)y = c_l a₂- a_tc₂ b,(c,a₂— «,c₂)

■ a_l(b_la₂ — a, b₂ p^y stosownych założe-niach.

b, a₂ — a, b₂

i) Metoda wyznaczników polega na obliczeniu trzech wyznaczników i zastosowaniu ich do wzorów na .x i y,

A B |HH

to liczba obliczona w naste-

x = t;—

(wyznacznik: pujący sposób:

C D A

C ,

= AD — BC). na przykład:

", * + b, y = c, a,x + b, y = c.

	^c,	by
WM	Cy	by
^x w	",	by
	°2	ijy
	",	c,
wr	(łj	f.
^ym W '	a,
	U,	b.

przy stosownych założeniach.

Uwaga: W g), h). i) potrzebne są stosowne /“b^v żenia — jakie i co ma miejsce w przypadku ich bra ku jest omówione w 3.1.6.