CCF20090228024

Wpływ strat w elementach filtrów

W przypadku FPP elementami składowymi filtru są obwody rezonansowe lub rezonatory. Korzystając z transformacji częstotliwości (9.21) można przeliczyć dobroć rezonatora O_k na równoważną dobroć Q elementu w prototypie FDP.

Q_k = wQ_k’    (9.29)

Filtry wyjściowe w urządzeniach nadawczych powinny mieć małe straty wtrąceniowe, ponieważ tracimy w nich moc sygnału nadawanego, często wygenerowaną wysokim kosztem. W urządzeniach odbiorczych tłumienie sygnału wnoszone przez filtry wejściowe zwiększa wartość współczynnika szumów o wartość tłumienia wtrąceniowego filtru. Z tego względu zagadnie-nie minimalizacji strat wnoszonych przez straty w elementach filtrów jest w zakresie .w.cz. bardzo ważne.

W celu analizy roli strat w elementach FDP wprowadzamy pojęcie współczynnika strat d_k A-tego elementu filtru

Q_k = L_k/R_k = CO] C_klG_k = coi/d_k    (9.25)

Korzystając z (9-25) możemy zapisać impedancję gałęzi szeregowej oraz admitancję gałęzi równoległej FDP w postaci

4 = L',(j ca +d_k) Y'_k = C;G co +d_k)    (9.26)

co prowadzi do przedstawionej na Rys. 9-38 modyfikacji układu FDP z Rys. 9.19(a). Zgodnie z (9.26), przy' częstotliwości zerowej w układzie z Rys. 9.38 pozostają tylko elementy rezystancyjne.

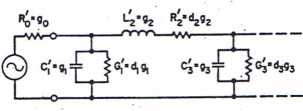
Rys. 9.38. Fragment prototypu FDP uwzględniającego straty w elementach.

Można wówczas przeprowadzić uproszczoną analizę wpływu strat w elementach, która prowadzi do następujących wzorów na przyrost tłumienia wtrąceniowego (A/4)₀ filtru przy częstotliwości zerowej

(A/l)o = 20 log (C„ + 1) [dBj    (9.27)

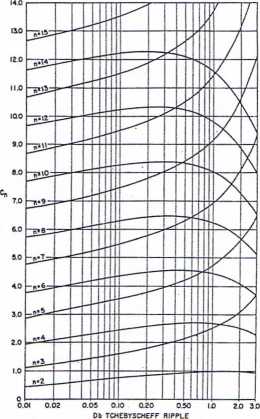
jeżeli współczynniki tłumienia wszystkich elementów filtru mają taką samą wartość d. Wartość współczynnika C„ odczytujemy z Tabl. 3 dla filtrów o charakterystyce maksymalnie płaskiej lub też z wykresu na Rys. 9.39 dla filtrów o charakterystyce równomiernie falistej.

Rys. 9.39. Współczynniki C„ dla filtrów o charakterystyce równomiernie falistej.

Dzięki temu tłumienie wtrąceniowe FPP przy częstotliwości środkowej filtru można natychmiast obliczyć na podstawie wartości O_k’, (9.29), (9.27) lub (9.28). Warto zauważyć, że dzięki wprowadzeniu inwerterów w FPP można stosować niemal identyczne rezonatory o takiej samej wartości O_k. W związku z tym w przypadku FPP często uzasadnione jest stosowanie zależności (9.27).

n

9.7. Rozgałęzienia 3-wrotowe

(AT)₀ = 4.343 Z d_kgk [dB] -(9.28) A—1

jeżeli chcemy uwzględnić różne wartości współczynników tłumienia poszczególnych elementów (co w przypadku FDP ma na ogól miejsce).

Ponieważ dobroć elementów FDP zależy od częstotliwości a w układzie zastępczym filtru pojawiają się reaktancje, tłumienie absorbcyjne filtru zmienia się z częstotliwością. Rzeczywiste charakterystyki filtru możemy przewidywać, wprowadzając straty do modelu filtru, np. w PUFF-ie.

Idealne rozgałęzienie 3-ch identy cznych prowadnic falowych

Rys. 9.40.

Macierz S rozgałęzienia o pomijalnych rozmiarach

-		»	cn
1	1.00	9	5.76
2	1.41	10	6.39
3	2.00	11	7.03 .
4	2.61	12	7.66 "
S	3.24	13	8.30
6	3.86	14	8.93
7	4.49	15	9.57
8	5.13

1/3	2/3	2/3
2/3	1/3	2/3	(9.30)
2/3	2/3	1/3

Jest to rozgałęzienie niedopasowane!

Tabl. 3. Współczynniki C„ dla filtrów o charakterystyce maksymalnie płaskiej.