CCF20120509100

Po podstawieniu danych liczbowych otrzymamy

y?=7(f+y(5óp+^

Obliczona zatem średnica przewodu zastępczego wyniesie

d - 83,44 mm.

5.3. Pompa w układzie przewodów

5.3.1. Prędkość średnia oleju w przewodzie

4-50

c =

4Q ₌_

nd² 3,14 • (1)'

= 63,7 cm-s^-1.

a liczba Reynoldsa

cd 63,7-1

^Re = —= -^r = ³¹⁸. v 0,20

Z obliczonej wartości liczby Reynoldsa wynika, że przepływ oleju (przy założonym natężeniu przepływu) jest laminarny. W związku z tym ciśnienie tłoczenia wyznaczamy z przekształconego wzoru Hagena:

<2 =

ngj d^A 128 v

(I)

stąd spadek hydrauliczny

(2)

128 v<2 ng d^A

Ponieważ

J =

A h

(3)

oraz

Ah = —, PG

więc

J =

pgi'

r>)

Z porównania zależności (2) i (3) wynika następujące równanie:

p 128 vQ pgl ngd^Ą

z którego po uproszczeniu i przekształceniu wyznaczamy szukane ciśnienie

P =

l2SvQpl nd⁴

p = 21034 Pa w 0,021 MPa.

Po podstawieniu danych liczbowych otrzymamy 128•20•10^-6■50•10“⁶•860-6

3,14 (0,01 )⁴

5.3.2. Dla przekrojów 1 (zwierciadło cieczy) oraz 2 (otwór ssący pompy) (rys. 1-5.26) układamy uogólnione równanie Bernoulliego, a zatem:

c\ p, _n c\ p,

-± + Łl ₊ o = -L + !!± + H + I.h_s,

2g pg 2 g pg

gdzie

cl J

= M- + C_s + 2C_t ,    C,=0,    p₁-p₂ = p, C₂ = c =

2 g \ d

46.

nd²’

sląd

H-i- ¹⁶²

/

2,4 _ I 1 + ² — + £_s + 2

pg n²d*-2g\ d ⁵ k

Po podstawieniu wartości liczbowych otrzymamy

H = 3,58 m.

5.3.3. Prędkość wody w rurociągu

3,54 m-s ¹,

4 Q    4 0,01

nd² n (0,06)²

it liczba Reynoldsa

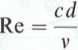
3,54 • 0,06 10“⁶

= 212400.

Przepływ wody jest burzliwy, zatem współczynnik strat na długości obliczamy / następującej formuły Blasiusa:

0,3164

f/Re

0,3164 </212400

0,0147.

Wysokość rozporządzalną (pompowania) H_z, jaką musi wytworzyć pompa w celu przetłoczenia żądanej objętości wody Q, wyznaczymy z uogólnionego równania lln noulliego, sformułowanego dla przekrojów 7 i 2 (rys. 1-5.27), a zatem

h 2 4- /i 3 H"^4 4" £ h_s.

M) Pd    2 g pg