DSCF2532

4 ftasnde i pewse wtefflotó prawdopodobieństwa

pierwszy gracz meae otrzymać f^J składów kart.

drsc gracz soźe c trr- tuic    I 1 układów kart.

\13/

_t__. _ .    i.m

irzEc pacz boże otrzymać | _r. I aHądów kart _r

i 12^

owacty zrzez msae otrzymać |_u|=i ijiać bn. ^afcrae priwdopodbiaeiwc jest wiec równe

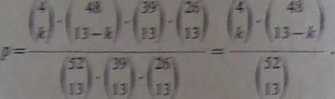
>«ieźr z kolei odpowiedzieć na pytaaśe: jakie jest praiwdopodofciemtaro, źe * tack tJobraayek losowo z taii będzie fc asów? Stwierdzamy, że do układu tych

* A    f//%** .*'5?^    /

wfe «ók < spośród czKiakasów LJsosobaisi i IW twych kart |    ~ I sp<

*cść wszystkich mo&Bwyck okładów U kart jest równa |_f~) kombinacjom, a kasę prawdopodobieśstww

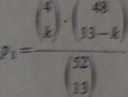
Zachodzi wiec równość uzyskanych wynifco**.

Jest rzeczą widoczną, kr przypasywanie znaczenia porządkowi w okładzie

zmienia otrzymanego wynika. Lwzgkgdniaśąc to zaważymy, że każda z LI ko

> ;»•/•>• ".''/..i hyć .">^'.‘uv'*'-sna VI--_s *pc$ehaww na 13 mielcach. Sa pozostałych 9 r *tmeje jpwobów roefefcwwaaia reszty kart. lent K*| różnych cifcłłdó* w których porządek odgrywa role. a zatem prawdopodobieństwo /t będzie rów;

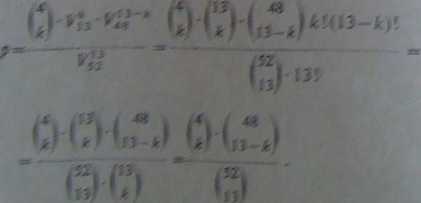
Pkzykłaó 4.8A^ talii 24 kart losujemy jednocześnie 5 kart. Jakie jest prawdopodobieństwo ^(iy^Knenia 4 polegającego na tym, źe wśród wylosowanych kart otrzymamy trzy karty pikowe?

Rozwiązanie. Zakładamy, źe każdy okład pięcia kart jest jednakowo moźfiwy. Zbiór podstawowy składa się z takich pięcioelementowych kombinacji (kolejność kart

nic odgrywa rołt>, źe powtórzenia są niemożliwe (ciągniemy jednocześnie), tzn. z | j

kombinacji. Sprzyjającymi są te zdarzenia elementarne, które polegają na otrzy maniu

układa, w skład którego wchodzą trzy piki i dwa nieprkr. Ilość takich układów jest równa

ilości sposobów, jakimi można wybrać trzy piki z sześciu i dwa nieptlri z pozostałych

_    ,    _    .    /Sj /J9v _    /Iffj

15 kart. Bose ta jest równa iloczynowi kombinacji j,} r { ^ j. tj. |^| rl^La szokane

prawdopodobieństwo wyrazi się liczbą

PM)=

H3

(24\

Przykład 4.2.5. Cfofczyć prawdopodobieństwo p tego, źe wśród 13 kart pobranych losowo z talii 52 kart będzie dokładnie £ czerwonych kart, gdzie £—0,1,2,..... 13.

.    - - Z⁵²)

Rozwiązanie. Kart czerwonych jest tyle co czarnych, tj. 26. Istnieje (    | różnych

13-efermentowycfe okładów kart wybranych z 52-ełementowej tahi.

. (26\

7f zbioru czerwonych kart £ czerwonych kart może tworzyć | , I różnych okładów,

/ 26 » ,

przy czym !3-£ pozostałych czarnych kart będzie tworzyć | łakich układów. Liczba

IVl I fest zatem ilością wszystkich różnych układów kart, wśród którvch £ jest 'ł '

czerwonych, czyli

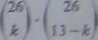
p* —

jest szukanym prawdopodobieństwem- . -

Przykład 4.2.6. Obliczyć prawdopodobieństwo p tego, źe spośród grających w bridźa pieńmy gracz otrzyma o, drugi 6, trzeci r, a czwarty </ asów (n-f 6+c-i-d= 4). Rozwiązanie. Mamy

p=