DSCF2523

4. Pojęcie i pewne własności prawdopodobieństwa

102

Napiszmy powyższy wzór dla n»I, 2*3,... Mamy

i-«+b    ,    ,. :    b /w_a .x

/ b V ! i

11 p|j -»+*=[(?>- jMl |i 1|§    11it|-

/ b \,    * b

I 1—a + b/    1—a+b

Załóżmy, że

+ b

p-=(^pndh)⁽““^6r‘⁺r^

Wykażemy, że

P-+i

/ b l ■ i

_ł__g • ilteil I

+ b

Mamy

P«+i=P.(a--b)+b

1—fl + b

ab — b² + b—ab + b²

BPill

y 1-a + b/

co po redukcji kończy dowód. «

Uzyskany tu ciąg prawdopodobieństw jest najprostszym przypadkiem tzw. „łańcucha Markowa”. Przy przejściu granicznym, gdy n-*oo, otrzymujemy

P=lim p„=

H~*eo

b

1—a + b

Ciekawy jest fakt, te p nie zależy od początkowej wartości p_x.

Przyioad 4.5.8. Niech prawdopodobieństwo, że po wyjeździe z domu napotkamy na pierwszym skrzyżowaniu zielony sygnał świetlny, będzie równe 0,5. Sygnalizacja jest tak ustawiona, że w przypadku zatrzymania się na dowolnym skrzyżowaniu przy świetle czerwonym prawdopodobieństwo tego, że na następnym skrzyżowaniu zastaniemy światło zielone jest równe 0,95, natomiast prawdopodobieństwo tego, że jeśli na dowolnym skrzyżowaniu będziemy mieli światło zielone, to i na następnym będziemy mieli światło zielone, jest równe 0,3.

1.    Obliczyć prawdopodobieństwo, że po wyjeździe z garażu na trzecim skrzyżowaniu będziemy mieli światło zielone.

2.    Obliczyć prawdopodobieństwo graniczne.

Rozwiązanie. Korzystając ze wzorów otrzymanych w przykładzie 4.5.7 otrzymu-

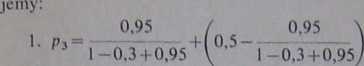
• (0,3 -0,95)²« 0,608.

2. || 0,576.

Przykład 4.5.9. Dwaj zawodnicy A i B grają w warcaby. Umówiono się, że pierwszy

na korzyść tego, który ma pierwszy ruch. Obliczyć prawdopodobieństwo, że A wygra w n-tej rozgrywce.

Rozwiązanie. Oznaczmy przezp_n prawdopodobieństwo, że A wygra w n-tej rozgrywce, więc 1 *-/>„ jest prawdopodobieństwem wygranej gracza B. Prawdopodobieństwo, że A wygra n-tą grę i wygra (w-j-l)-szą grę jest

k

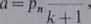
gdyż A zaczynał (n+ l)-szą grę.

Prawdopodobieństwo, że A przegra n-tą grę i wygra (n+l)-szą grę jest

k+1

*>=0-A,)7-

gdyż B zaczął pierwszy (/? + l)-szą grę z szansą przegrania -----Całkowite prawdopo-

/c 1

dobieństwo wygrania przez gracza A (/H-l)-szej rozgrywki jest

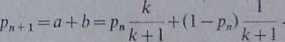
Z powyższego otrzymujemy ostatecznie po rozwiązaniu odpowiedniego równania różnicowego

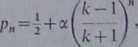
gdzie ot = 2, gdy pierwszy rozpoczyna grę zawodnik A, natomiast a =—5 w przeciwnym przypadku.

§ 4.6. Niezależność zespołowa. Omówione w paragrafie poprzednim zagadnienie niezależności dotyczyło niezależności między dwoma zdarzeniami. Gdy liczba zdarzeń jest większa, to niezależność w dotychczasowym sensie dotyczyć będzie poszczególnych par zdarzeń. Oprócz tego badać można niezależność między grupą zdarzeń. Terminologicznie ujmujemy to, mówiąc o niezależności parami i niezależności zespołowej (en bloc). Ta ostatnia wymaga z kolei dokładnego omówienia. Następująca definicja precyzuje omawiane pojęcie.