DSCF2520

96

4. Pojęcie i pewne własności prawdopodobieństwa

PRZYKŁAD 4.5.3. Na każdej z pięciu kartek napisano jedną z cyfr: 1, 2, 3, 4, 5 p bieramy losowo i bez zwrotu trzy kartki. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że suma otrzymanych cyfr będzie Liczbą parzystą?

Rozw iązanie. Uzyskanie z danego zbioru cyfr ich sumy jako liczby parzystej j_est możliwe w przypadku natrafienia na dwie kartki z cyframi nieparzystymi i na jedną kartkę z cyfrą parzystą, występującą bądź w pierwszym, bądź w drugim, bądź w trzecim losowaniu. Oznaczmy przez ,4* zdarzenie polegające na otrzymaniu cyfry' parzystej w A:-tym losowaniu (A: = 1,2, 3\ przez A_k — cyfry nieparzystej. Mamy wówczas

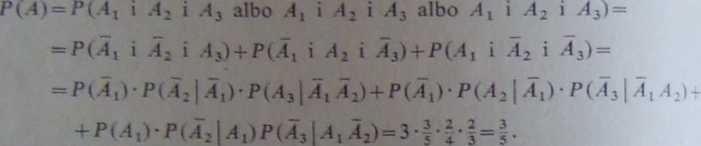
Rozwiązanie powyższe należy porównać z rozwiązaniem przykładu 4.1.7.

Definicja 4.5.2. Mówimy, że zdarzenie A jest niezależne od zdarzenia B, jeśli zachodzi jeden z dwu przypadków:

(4.5.4)

1.    P(A\B)=P(A) i P(B)>0,

2.    P(B)=0.

Jeżeli P(.4jB)>P(_J4). to mówimy, że zajście zdarzenia B wpływa pozytywnie na zajście zdarzenia A. natomiast, jeżeli P(i4|B)<P(4), to mówimy, że zajście zdarzenia B ma wpływ negatywny na zajście zdarzenia A.

Przykład 4.5.4. W pudełku są ołówki: 10 czerwono-niebieskich, 2 niebieskie. 7 zie- I lonych. 1 zielono-czerwony. Losujemy jeden ołówek.

1.    Jakie jest prawdopodobieństwo zdarzenia A_c polegającego na tym, że otrzyma- j nym ołówkiem można kreślić w kolorze czerwonym?

2.    Jakie jest prawdopodobieństwo kreślenia otrzymanym ołówkiem w kolorze czer- I wonytn. jeśli wiadomo, że ołówek ten rysuje: a) na niebiesko (zdarzenie zł„), b) na zielono (zdarzenie 4J?

Rozwiązanie. 1. Odpowiedź jest natychmiastowa, liczymy bowiem ilość wszystkich I ołówków i ilość tych ołówków, które mają kolor czerwony. Iloraz znalezionych wyników. 1 tj. ~ jest szukanym prawdopodobieństwem zdarzenia A_c.

2a. Obliczamy prawdopodobieństwo warunkowe zdarzenia A_e, przy założeniu, że zdarzenie A_m zaszło. Otrzymujemy:

Licznikiem ułamka jest liczba ołówków, którymi można kreślić na czerwono i na niebiesko, w mianowniku — ilość tych ołówków, którymi można kreślić na niebiesko* Zauważmy, że

§ 4.5. Prawdopodobieństwo warunkowe

97

czyli, że wiadomość o wyciągnięciu ołówka, którym można rysować kolorem niebieskim, zwiększyła prawdopodobieństwo rysowania kolorem czerwonym (wpływ dodatni — pozytywny).

2b. Analogicznie obliczamy prawdopodobieństwo natrafienia na ołówek, którym można rysować w kolorze czerwonym, jeśli wiemy, że można nim rysować w kolorze zielonym. W tym przypadku stwierdzamy, że

P(A_c\A_t)^l

czyli

P(A_C\A,)<P(A_C).

Wiadomość o wyciągnięciu ołówka rysującego kolorem zielonym zmniejszyła prawdopodobieństwo natrafienia na ołówek, którym można kreślić kolorem czerwonym (wpływ ujemny — negatywny).

Przykład^.5.5. W urnie znajdują się 3 kule białe i 4 kule czarne. Jakie jest prawdopodobieństwo zajścia zdarzenia B polegającego na otrzymaniu dwóch kul białych, przy założeniu, że losujemy z urny dwa razy i po pierwszym losowaniu kula nie zostaje zwrócona do urny?

Rozwiązanie. Oznaczmy przez Bi zdarzenie polegające na wylosowaniu kuli białej za pierwszym razem, a przez B₂ — kuli białej za drugim razem. Jak widać, zajście zdarzenia B₂ jest zależne od zaistnienia zdarzenia B_t. Zajście zdarzenia B_t zmniejsza szanse zajścia zdarzenia B₂, gdyż po wylosowaniu pierwszej kuli białej zmniejsza się ilość kul białych w urnie. Zajście zdarzenia B polega na łącznym zajściu zdarzeń Bi i B_z. Stąd

Twierdzenie 4.5.1. Jeżeli zdarzenie A jest niezależne od zdarzenia B, to zdarzenie B jest niezależne od zdarzenia A.

Dowód. Istotnie, ze wzoru (4.5.2) mamy

1)    P(B-A)=P(B)-P(A\B), przy założeniu, że P(B)>0 oraz

2)    P(A‘B)=P(A) P(B\A), przy założeniu, że P(4)>0.

Korzystając z pierwszego przypadku definicji 4.5.4 niezależności zdarzenia A od zdarzenia B otrzymujemy

3)    P{B A)=P{B) P{A).

Z 2) i 3) wynika równość

P(A)-P(B\A)=P(B)' P{A)_t którą dzielimy obustronnie przez P(A)>0, otrzymując

P(BjA)=P(B),

co świadczy o niezależności zdarzenia B od zdarzenia A.

Jeśli natomiast P(A)=0, to niezależność zdarzenia B od zdarzenia A wynika natychmiast na mocy drugiego przypadku definicji 4.5.2.

Jak to wynika z twierdzenia 4.5.1. własność niezależności jest dla zdarzeń A i B wzajemna (symetryczna). Uwaga ta skłania nas do przyjęcia następującego określenia: 7 Kombinatoryka...