DSCF2521

y» 4. Pojęcie i pewne własności piamiupv»

Definicja 4.5.3. O zdarzeniach A i B mówimy, że są wzajemnie niezależne, jeśli zachodzi jeden z dwu przypadków:

1)    gdy P(A)>0 i P(B)>0 oraz spełniony jest warunek 4.5.4, tj.

P(A\B)=P(A),

2)    prawdopodobieństwo co najmniej jednego ze zdarzeń równa się zeru

P(A)=0 lub P(£)=0.

Jeśli

(4.5.5)    P(A\B)jtP(A), gdzie    P(B)> 0,

to mówimy, że zdarzenia A i B są zależne.

Duże znaczenie praktyczne ma twierdzenie następujące:

Twierdzenie 4.5.2. Na to, aby zdarzenia A i B były niezależne, potrzeba i wystarcza, żeby prawdopodobieństwo łącznego zajścia tych zdarzeń było równe iloczynowi prawdopo-bieństw każdego z tych zdarzeń, tj.

(4.5.6)    P(A • B)=P(A) * P(B).

Dowód. Udowodnimy najpierw warunek konieczny, tzn. słuszność|twierdzenia: Jeżeli zdarzenia A i B są niezależne, to

P(AB)=P(A)P{B).

Mamy (wzór 4.5.2):

P(A-B)=P(A)-P(B\A)=P(B)-P(A\B).

Jeżeli zdarzenia A i 5 są niezależne, przy czym P(A)>0 i P(B)>0, to

P(£|,4)=P(jB) i PU|B)=P(y4), a więc P^A-B) — P(A)-P(B).

Jeżeli zdarzenia ^4 i B są niezależne na skutek tego, że P(,4)=0 lub P(£) = 0, to, p°* nieważ (własność 3.3.11) >4 *££.4, mamy z twierdzenia 4.3.1

P(/lB)<P(/!)=0, czyli P(A-B) = 0.

Zachodzi więc równość P(A B) = P(A) P(B).

Udowodnimy warunek wystarczający:

Jeżeli jest spełniona równość (4.5.6), to zdarzenia A i B są niezależne (*).

Jeżeli

PU)> 0 i    P(£)> 0,

(') Warunek ten może być przyjęty jako określenie zdarzeń niezależnych. Wówczas związki (4.5-11 lub (4.5.2) otrzymuje się jako twierdzenia.

to porównując wzór (4.5.6) ze wzorem (4.5.2), otrzymujemy P{B\A) = P(B)    i P(A\B)=P(A),

a zatem zdarzenia A i B są niezależne.

Jeżeli równość (4.5.6) jest spełniona, ponieważ obie jej strony są równe zeru, to P(A)= =0 lub P(B)=0, a więc zdarzenia A i B na mocy definicji 4.5.3 są niezależne.

Z pojęcia prawdopodobieństwa warunkowego korzysta się w twierdzeniu o tzw. prawdopodobieństwie zupełnym (zwanym również całkowitym).

Twierdzenie 4.5.3. Jeżeli zdarzenia A_lt A₂,..., A_n tworzą układ zupełny zdarzeń, to prawdopodobieństwo dowolnego zdarzenia B obliczamy ze wzoru

(4.5.7)    P(B)=P(A,)P(B\A₁)+P(A₂)P(B\A₂)+...+P(A_n)P(B\A_n)=

n

== i P(A_t)- P(B\Aj).

1=1

Dowód. Niech B będzie zdarzeniem należącym do algebry zdarzeń S utworzonej w przestrzeni /. Niech zdarzenia A_x, A₂, A_n tworzą układ zupełny zdarzeń, tzn.

Ai+>4₂ +... +A_n=I,

przy czym ApAj=0 dla /#./(/= 1, 2,..., n, j—l, 2, ...,»). Pomnóżmy obie strony tej równości przez B. Wówczas B I=B (aksjomat X) oraz B-(A_X + A₂ + ...+A„)=B A_l+ +B-A₂ +    A_n (aksjomat IX). Zatem

(4.5.8)

A_i'B+A₂'B + ...+A_n‘B=B.

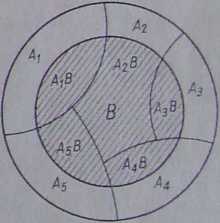
Wzór (4.5.8) oznacza, że zajście zdarzenia B jest równoważne zajściu tego zdarzenia z jednym ze zdarzeń A_x, A₂, A_n. Rysunek 4.5.2 ilustruje ten fakt dla n=5. Zdarzenia A_XB, A₂-B, ..., A_n B również wykluczają się parami, gdyż

' (A_r B)-(Aj-B)=A_i Aj-B=(Ai Aj) B=0 B=0

dla i^j (aksjomaty V i VII, własność 3.3.2). Wobec tego

P(B) = P(A_lB) + P(A₂B) + .,. + P(A_nB).

Z (4.5.2) mamy

P(A_kB) = P(A_kyP(B\A_k),    k = 1,2,

1HKHI i . ...    ¹    Rys. 4.5.2

co uwzględniając otrzymujemy natychmiast wzór (4.5.7).

Rozszerzymy obecnie pojęcie układu zupełnego zdarzeń na przypadek algebry prawdopodobieństwa [/, S, P], gdzie I może być zbiorem o dowolnej liczbie elementów.

Definicja 4.5.4. Mówimy, że ciąg zdarzeń A_n («= 1,2, ...) należących do S tworzy układ zupełny w szerszym sensie, jeżeli wykluczają się one parami, tj.

A_t’Aj=0 dla    (i = 1,2,..., j—1,2,...)

7*