DSCN1167 (2)

7.23. Wskazówka.Z podanych założeń wynika, że 3 sin² a p cos2 P i 6 sina cos a = 2 sin 2 /?.

Dzieląc stronami powyższe równości otrzymujemy tga = ctg2/?, a stąd wynika teza.

7.24. Z warunków zadania wynika, że y = n — (a 4 P). Stąd cosy = — cos (a 4 p).

Zatem

sin²a 4 sin²/ł — cos (a — p) cosy — cos²y =

= sin²a 4 sin²/ł 4 cos(a—/?)cos(a + P) — cos²(a + P) —

— sin²a 4- sin²/? + - [cos 2a + cos 2P] — cos²(a + p) —

= sin²a 4 sin²P 4 j — sin²a 4 - — sin²^ — cos²(a 4 p) = = 1 — cos²(a 4 )?).

Stąd otrzymujemy równanie 1 — cos²(a 4 /?) = -,

czyli cos²(a 4 P) = Równanie to ma 2 rozwiązania w przedziale (0; n): a 4 P = - lub a 4 P = 7.

o    o

Wobec tego y = -7- lub y = 7.

6    o

7.25. Wskazówka. Założenie jest równoważne równaniu sin (a 4 p) cosa = 3 sina cos (a 4 /O, a teza jest równoważna równości 2 sin (2a 4 P) cos/? = 4 sin/? cos/?.

7.26. Wskazówka. Najpierw wykazać, że

sin²(t 4 x) 4 sin(t 4 y) 4 sin(r 4 2x — y) 4 - =

= sin² (t 4 x) 4 2 sin (t 4 x) • cos (y — x) 4 - i potraktować

nierówność opisującą zbiór A jako nierówność kwadratową względem zmiennej u = sin (t 4 x).

1    '    _ .    7r(3k + 1) n{3k + 2).    |1

4 = {(x, 11 x,ye.R i x +-r—- ^ y ^-1—-1 ke C}.

2 0n^:

Pole figury AnB jest równe liczbie

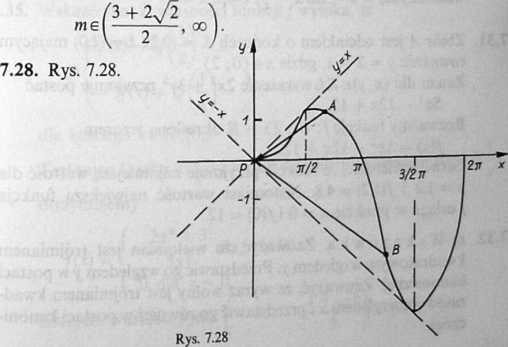
7.27. Przy ustalonym meR+ figura A_m jest kwadratem o wierzchołkach A = (m, 0); B — (0, m); C = (—m, 0); D — (0, — m\ natomiast

B_m jest kołem o środku S = (^, 0) i promieniu J~m. Stąd

natychmiast wynika warunek tn> bo w przeciwnym razie

środek koła B_m byłby punktem zewnętrznym lub punktem brzegowym kwadratu A_m.

Inkluzja B_m c A_m będzie zachodzić wówczas, gdy odległość środka S od boku AB i boku AD będzie większa lub równa od

1

/napromienia koła B_m. Stąd Jm<—■— Po rozwiązaniu tej

y/2

nierówności i uwzględnieniu warunku m > - otrzymujemy odpowiedź

191