Hellwig i grafy (11)

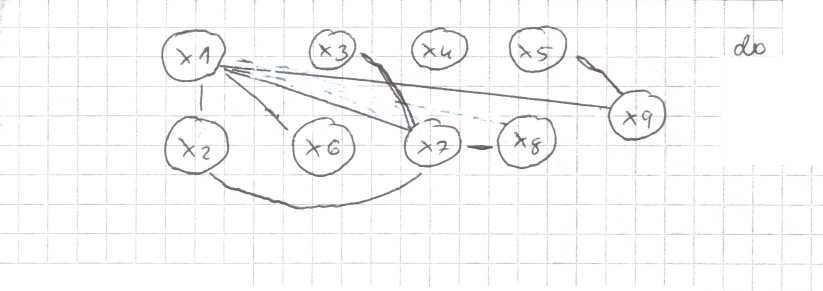
lad ALO

n

S ;

\ C

l_riOM io_tUW,flpLĄŚ

yy		L	IX/ YK	oc	<Oo	>cx

d& 'M^ac^yCat,

£

L

>	4 C	$_ 0			[yd )		\z)
0	>	^ 0			F~\/
0 0 .4				i Li u	&	W

i/A „». „,,,, ^••g^i,;o & 171 idiztrjrp,i<liir,    ist

i q U ^    n9 o n ai    /ni 1    ^u '

Jt)OsrcŁu €j

Ą

im

o

-oyi o

OJi

m

o

^J‘o

__rui

o O, W O

A

A

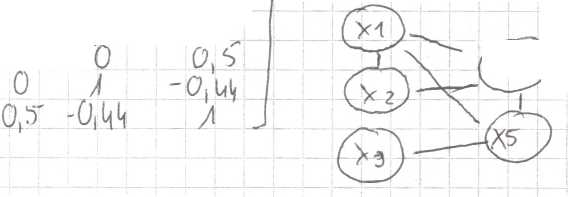
t£o

' y< 4 j nJi^yn^c^ ,X

( V) $OU

0

n

t

\MiW

- i

4l^j!, I^ł|    L-jfyjtljj]- 0,1^) || i p 4

, o......1 ^:ion o w

0 -m    i    o    O    6    -Oj<$

o.b" o    o    2    b    loi    ligi

0 o    o    O    4    10!    O

tui os ó o _ni_M

oj firi-ffisi | o loj 1/

eto WvQ(£jlLu-' <s€jcłą_IŁWhl^Hkjl g •    i |    ;__v /v-.

X 2 ( /igcjTif c£| LouAfeLJ f xrj$~ jf itole>Ł>&vi^ ^v ^

)

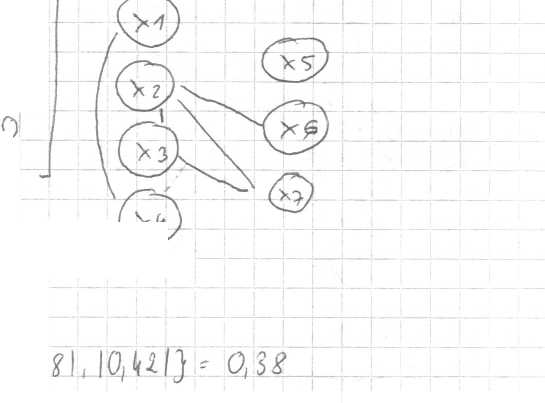
Zct dP ■ 2 A

u.

t

	-0,41/ J	0	0	0 Ov A-		—X	z
I	0 0		0	0 p	i	l
	0,3 . 0	0	yf	0 -ąw	1 V/, ^—	—r Xk
	0 0	0	0	' b
	jij mc	UL-	^yi.	0 A i	-UL-	x5

Al) Z do wud cLoJUc ^-Ojclo^ ■zwAAyey) v\#

y 3 i X ę ( j 'lo Co ycuie ) t' X u f *wsx

o) Łp^tiytiaL c - jLŁ (a zząM

'    \    •?    '-'A    \ 2

\u z -

\«^\vlud\ ■* UsjŁ-l L v ' —Xji

. U-»tI1 IfrjsL

L<b '-

U% I

UoUU “Ąoirl

Uyi-L-U U.. L

fel>r. j bpp M

_tV), -* likfel ^ UgsT i, & 3

L- ć,as:i 1 oUH V®_tĄW 1

m