Hellwig i grafy (8)

z-\Mstę vi we

cHo    ucstuóęlccj

*5- zyv) i<?\AT) OL i'w>^9i/iW °v.

X / - Ąxudu '<t^ *AlO^JsOUC(Asi 2 V

X -2 ' ISg.C&l brCUSfo^U.- ________ _

T-Ct-d. X Ol

h - XxX_s Xu

Irt

U-m h i

- _X4_i

AA

>U-

.■•M^ r- y,3/^

__ ₌ j&i. . om

Źfl

_—- ,    , C[ 2^6

■* Iik\ I    2/0

_____{_} u. f 1    0,4 IS

I ¹ I -rt^Ł, I    £

I ¹ l-r-ji* _____

-- o₍X}X,+ O, 2?ć H O, X2-X - 0,05-2

9-O.d. 02)

k* l"-J: Ib

Vi

lo

xx - y w

| -t

^y1A

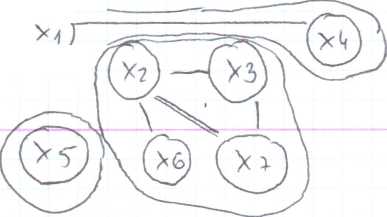
b^^rX/i ^a^TX-z x $ * x $ U - y_u k, r~ y a x 2    * X/f x

^ 6 ¹ X /j X t( l< ■ X z X 2> ^ s - X 2 X 4 U ‘ X/|    Xq U ix ^: X 2 X■$ Xit U>{ 3

Wu - X/( X 2 X 3 Xti

gX© i«7,2 0W ^Ł _ O, 3l£

x,<w ;

_ - a, 1(5² 0,XOQ

x,^

2 ^w6 ‘    ^ 3

^;X" 5X1/    ^-ic?' A/f XzX3

*A X, Xj,.- .

I T₁| | i 1^22 |    /f/^O

!{,* O, 3 2 g -* OjOU •' 0X«

X. X

X 2. h xa

w X, 3

jyj* x, u '

_ i^isT _r 0,^

W3.^ h 5?31    "X ^2.

>W,3

0₍ Ł,

43

¹ '3/f I ¹ r i i I    i    .

U₂ t O, i<7X-ł O, 39 G - O, £0 9

4.vi^'evivux X/l X 3    a 5 ku'cc l( \^oXO<>l>cma^ e    _%\ma.€vi^€^ ub j cx S t/W puv> ćj

(iyi fh fru. pO\eiMv^ośc^/ vui>śv>ilću >wfj

" X (W	o.w A	0 0	0 0,55	®-	5©
0 L 0	0 0fi5	/ 0	0 / J	©r	©

X>) Of VKUvO (I O^sl,lo,<15}, IO,5|,|C15S(y« 0,5 l-r,'j I <f 0,£ * O d'

Wij | ^> O, *7 ^; U.j )