str151

b BaikicwKż-OJiibowfiiH. Z Mikulski, "gritno. W^iwawa 2f.K)5
ISBN 83 0l-l4579-X.Oby WN PWN 2005
gdzie: v - prędkość filtracji, k - współczynnik filtracji, i - spadek hydrauliczny (/ = (/?, - /?,) / /; rys. 128). Przy spadku hydraulicznym i = 1 prędkość filtracji jest równa współczynnikowi filtracji (v = k).
Jak widać z prawa Darcy’ego, podstawowe znaczenie dla ruchu wody w gruncie ma współczynnik filtracji, charakteryzujący stopień przepuszczalności utworów budujących strefę saturacji. Utwory, których współczynnik filtracji jest większy niż 10-? cm/s, są uważane za wodonośne.
Ruchem wód w warstwach wodonośnych „kierują” utwory trudno przepuszczalne. W przypadku poziomów wodonośnych o zwierciadle swobodnym dlatego, że stanowią jego spąg; w przypadku wód wgłębnych dlatego, że nakrywając zwierciadło tych wód od góry. wymuszają jego ugięcie.
Ilość przepływającej wody podziemnej oblicza się wykorzystując wzór Darcy'ego. Początkowo należy obliczyć natężenie przepływu jednostkowego, tj. tę ilość wody, która przepływa w jednostce czasu przez poprzeczny przekrój warstwy wodonośnej o szerokości I m, czyli
q = k • i • h • Z?,
gdzie: ą - jednostkowy przepływ wody (m3s ’),/?- wysokość warstwy wodonośnej (m), - szerokość przekroju (1 m), k - współczynnik filtracji (m/s), i - spadek hydrauliczny. Gdy miąższość warstwy wodonośnej nie jest stała, należy obliczyć jej średnią wartość Ohr) (rys. 129)
zależność ta oznacza jednocześnie jednostkową powierzchnię przekroju o szerokości I m.
Rys. 129. Obliczanie objętości przepływu wody podziemnej w jednorodnej warstwie wodonośnej; I, II - piezometry, hu h2 - miąższości warstwy wodonośnej. k - współczynnik filtracji, / - odległości między piezometrami
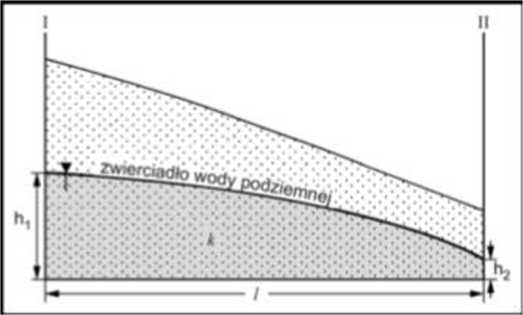
Spadek hydrauliczny określa zależność
i =
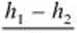
/
I5l






Cl
C
C
CO
o
3
a>

co
co
co
Wyszukiwarka
Podobne podstrony:
str151 b BaikicwKż-OJiibowfiiH. Z Mikulski, "gritno. W^iwawa 2f.K)5 ISBN 83 0
20751 str150 b BaikicwKż-OJiibowfiiH. L Mikulski, "gritno. W^iwawa 2f.K)5 ISB
str145 b BaikicwKż-OJiibowfiiH. Z Mikulski, "gritno. W^iwawa 2f.K)5 ISBN 83 0
str146 b BaikicwKż-OJiibowfiiH. Z Mikulski, "gritno. W^iwawa 2f.K)5 ISBN 83 0
str150 b BaikicwKż-OJiibowfiiH. L Mikulski, "gritno. W^iwawa 2f.K)5 ISBN 83 0
41270 str145 b BaikicwKż-OJiibowfiiH. Z Mikulski, "gritno. W^iwawa 2f.K)5 ISB
37550 str147 b BaikicwKż-OJiibowfiiH. L Mikulski, "gritno. W^iwawa 2f.K)5 ISB
str148 b BaikicwKż-OJiibowfiiH. L Mikulski, "RÓlrni. W^iwawa 2f.K)5 ISBN 83
str45 F. Bajkicwtcz-Grabowiki. Z. Mikulski. Hydrologia ogólna. W;irj/aw;i 200S ISBN 83-0l-l4579-X.«
60605 str233 F. Bajkicwtcz-Grabowiki. Z. Mikulski. Hydrologia ogólna. W;irj/aw;i 200S ISBN 83-0l-l45
str181 F. Bajkicwtcz-Grabowiki. Z. Mikulski. Hydrologia ogólna. W;irj/aw;i 200S ISBN 83-0l-l4579-X.«
str208 & F. Bajkicwtcz-Grabowiki. Z. Mikulski. Hydrologia ogólna. W;irj/aw;i 200S ISBN 83-0l-l45
str223 F. Bajkicwtcz-Grabowiki. Z. Mikulski. Hydrologia ogólna. W;irj/aw;i 200S ISBN 83-0l-l4579-X.«
str232 F. Bajkicwtcz-Grabowiki. Z. Mikulski. Hydrologia ogólna. W;irj/aw;i 200S ISBN 83-0l-l4579-X.«
str247 F. Bajkicwtcz-Grabowiki. Z. Mikulski. Hydrologia ogólna. W;irj/aw;i 200S ISBN 83-0l-l4579-X.«
więcej podobnych podstron