3582320729

6. CAŁKI POTRÓJNE

6.1 CAŁKI POTRÓJNE PO PROSTOPADŁOŚCIANIE

Oznaczenia w definicji całki pa prostopadłościanie:

P = {(x,y,z): aś x ś b, c śy ś d, p ś z ś q} - prostopadłościan w przestrzeni;

P = {Pj, Pz .... P„} - podział prostopadłościanu P na prostopadłościany P*. 1 ś kś n, przy czym prostopadłościany podziału całkowicie wypełniają prostopadłościan P i mająparami rozłączne wnętrza;

Axfa Ay* Az* - wymiary prostopadłościanu P*. 15 kś n;

d_k =y/(Ax_k)² +(Ay_k )² + f Az_k )^J - długość przekątnej prostopadłościanu P*, 1 ś k ś n; 8(P) = max{c5<: 1 ś kś n } - średnica podziału P;

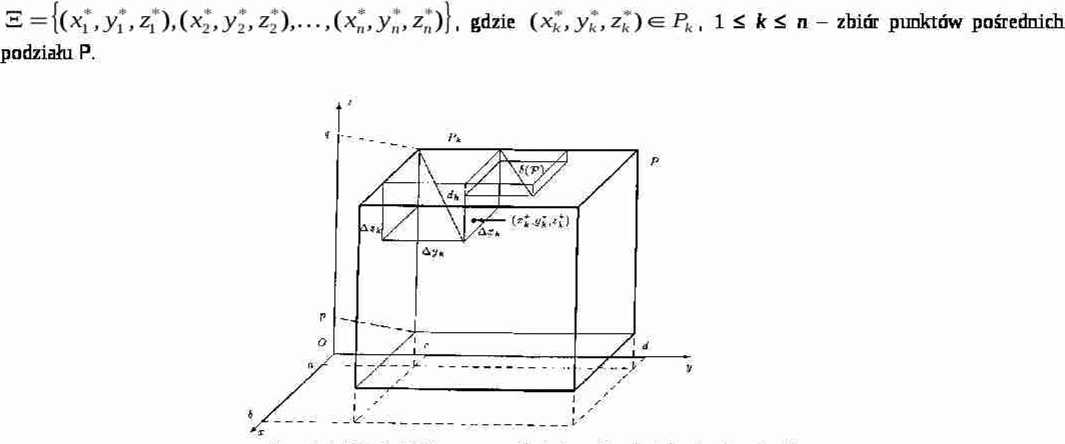
Rys 6.6.1 Podział P prostopadłościanu P = [a,b] x [c.d] x [p,q]

Def. 6.1.1 (całka patrójnapa prostopadłościanie)

Niech funkcja f będzie ograniczana na prostopadłościanie P. Całkę podwójną z funkcji fpo prostopadłościanie P definiujemy wzorem:

rrr    ^def    "

JJJ f^(x’ y> ^z')^dxdy^dz =    , Z*k )(Ax_k )(Ay, )(Az,) _t

o ile granica po prawej stronie znaku równości istnieje oraz nie zależy od sposobów podziału P prostopadłościanu P, ani od sposobów wyboru punktów pośrednich S. Mówimy wtedy, że funkcjafjest całkowalna na prostopadłościanie P.

Uwaga Całkę potrójną z funkcji fpo prostopadłościanie P oznaczamy też symbolem ffif(x,y,z)dV

_P

Fakt 6.1.2 (o całkowaniu funkcji ciągłej)

Funkcja ciągła na prostopadłościanie jest na nim całkowalna

Tw. 6.1.3 (o liniowości całki)

Jeżeli funkcje fi g są całkowalne na prostopadłościanie P oraz c e R, to:

a)    funkcja f + g jest całkowalna na prostopadłościanie P oraz

[JJ( f(x, y, z) + g(x, y, z))dxdydz = |JJ f(x, y, z)dxdydz + JJJg(x, y, z)dxdydz.

P    P    P

b)    funkcja cf jest całkowalna na prostopadłościanie JP oraz

JJJcf (x, y, z)dxdydz = cJJJ f (x, y, z)dxdydz

p    p

Tw. 6.1.4 (o addytywnośd względem obszaru całkowania)

Jeżeh funkcja f jest całkowalna na prostopadłościanie P, to dla dowolnego podziału prostopadłościanu P na dwa prostopadłościany P_3l P₂ o rozłącznych wnętrzach, funkcja f jest całkowalna P_} i P₂ na oraz