4037603088

Adam Bodnar: Wytrzymałość Materiałów. Osiowe rozciąganie i ściskanie

yl²

max u=u(l)=Al=-

2 E

Przemieszczenia są kwadratową funkcją współrzędnej x i osiągają swą największą wartość na końcu pręta, przy czym wartość ta nie zależy od pola przekroju poprzecznego pręta. Wykresy poszukiwanych funkcji pokazuje rysunek poniżej.

		N(x)	ax(x)	«w
	■	-7 Aly	-7 ^lr
	*		W
			f	\ yl^1
				_\ 2 E

Długość zerwania l_R to długość pręta, obciążonego jedynie ciężarem własnym, przy której największe w nim naprężenia normalne będą równe wytrzymałości na rozciąganie (można powiedzieć: długość przy której zerwie się pod ciężarem własnym).

Zatem:

max<7 =R_m -l_R y —3> l_R =^^sl

r

Jak widać długość zerwania l_R jest stałą materiałową. Przykładowe wielkości długości zerwania: drewno sosnowe 13.5 km, stal niskowęglowa 4.8 km, stal wysokowęglowa 9.1 km, duraluminium 16.9 km .

q =250 kN/m

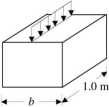
Przykład 9.8.3. Na 1 m długości ławy fundamentowej o przekroju prostokątnym bxh wykonanej z betonu o ciężarze objętościowym y = 22 kN/m³ przekazuje się równomiernie rozłożone obciążenie ze ściany q = 250 kN/m. Wyznaczyć potrzebną szerokość fundamentu b jeśli jej wysokość h = 1.5 m, a wytrzymałość obliczeniowa gruntu na ściskanie, na którym jest on posadowiony wynosi R_c,_g = 0.2 MPa

Rozwiązanie

Siła przekazywana z fundamentu na grunt wynosi: /V = q * 1 + y * h * b * 1

Z warunku nośności wynika:

q*\+y*h*b*\^_R b* 1

250* 10³ +22 * 10³ b

1.5 *b

<0.2 *10⁶

b > 1.5 m.

Przykład 9.8.4. Nadproże wykonane z belki dwuteowej I 200 przekazuje na mur obciążenie w postaci siły P = 60 kN. Obliczyć potrzebną długość oparcia belki przyjmując, że naprężenie obliczeniowe muru na ściskanie R_c__m = 2.0 MPa.

85