4037603095

Adam Bodnar: Wytrzymałość Materiałów. Osiowe rozciąganie i ściskanie

- ^E \ v	{£x+£y +fjj -> (7x=Eex,
°^x~i+vl^x \-2v
e r v	(ex +£y +£z ) j -> £TV =0 ,
^<7y~\+v\^£y \-2v
e r v !	4_ p _i_ e 1 _^ rz —0
°^z l+v[^£z \-2v	Ic.TC.TC./ 7 (J - — W ,
*xy =GyXy 'Cxy ’■	=0; Tyl=Gyyz -> ry!=0;

Należy teraz wrócić do równań równowagi (9.2) w celu sprawdzenia czy otrzymane w oparciu o przypuszczone pole przemieszczeń naprężenia spełniają te obiektywne zależności i aby wyrazić siły wewnętrzne poprzez siły zewnętrzne.

Zerowanie się naprężeń stycznych powoduje, że równania drugie, trzecie i czwarte są spełnione. Z równania pierwszego otrzymamy

jja_xdA=N —» jjEe_xdA=N, a ponieważ pole odkształceń jest jednorodne, to

A    A

odkształcenia liniowe są równe:

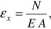
(9.3)

i naprężenia normalne wynoszą:

(9.4)

N

<7, = — .

* A

Wstawiając powyższe do dwóch ostatnich równań równowagi otrzymujemy:

t/M-⁰

~ jjydA =0

JJ<7jZć/a=o    —»

^-cr_xydA=0 -»

A bo osie (T, Z) są osiami centralnymi i momenty statyczne przekroju poprzecznego liczone względem nich są równe zero. Tak więc ostatecznie macierze naprężeń i odkształceń przy osiowym rozciąganiu mają postać:

	'N/A	0	0'		^n/ea	0 0 '
Ta =	0	0	0	, Te =	0	-VN/EA 0
	0	0	0		0	0 -VN/EA

W praktyce inżynierskiej bardzo ważne jest określenie wydłużenia pręta, czyli przemieszczenie jego końca AL Jeśli pole przemieszczeń w pręcie jest jednorodne to łatwo wyznaczymy zmianę jego długości bez potrzeby całkowania odkształceń:

(9.6)

Al N ^x~ 1 ~ EA

73