4037603093

Adam Bodnar: Wytrzymałość Materiałów. Osiowe rozciąganie i ściskanie

|| a_x dA = N, || dA =0, jj T^dA = 0,

|| (- r_xy z+r_xz y)dA = 0, || a_xz dA = 0, ||- o _x ydA =0.

Równania (9.2) możemy nazwać równaniami równowagi, gdyż wynikają z twierdzenia o równoważności układów sił wewnętrznych i zewnętrznych udowodnionego na podstawie warunków równowagi układu sił działających na ciało.

Z równań (9.2) nie można wyznaczyć <J_X, t_xy,Z_xz, gdyż to funkcje trzech zmiennych i aby je określić, zajmiemy się analizą deformacji bryły po przyłożeniu obciążeń. W oparciu o przyjęte założenia odnośnie materiału, jak i hipotezę płaskich przekrojów Bemoulliego przyjmiemy, że obraz deformacji pręta po przyłożeniu obciążeń jest taki jak to pokazuje rys. 9.2.

konfiguracja

początkowa

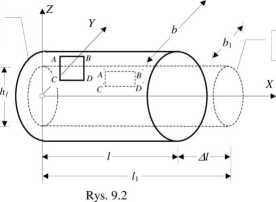
konfiguracja

aktualna

h

Analizując ten obraz deformacji pręta po przyłożeniu obciążeń przyjmiemy, że:

•    pole przemieszczeń jest w nim jednorodne,

•    odkształcenia kątowe włókien równoległych do osi układu odniesienia są równe zero,

•    odkształcenia liniowe związane są zależnością: £_y =£_z =~V£_X.

Powyższe obserwacje pozwalają napisać następujące zależności:

_ Al_ _ lj-l_ _ Ab _ b_x-b _ Ah _ h_x-h I ~ l '    ^y~ b ~ h '    ^z~ h ~ h '

r„=o, r„= o. o.

Nazwiemy je równaniami geometrycznymi gdyż są wynikiem analizy geometrii pręta po deformacji.

Mając odkształcenia możemy, korzystając z równań fizycznych Hooke’a, wyznaczyć elementy macierzy naprężeń:

72