4037603100

Adam Bodnar: Wytrzymałość Materiałów. Osiowe rozciąganie i ściskanie

o—£. Wykres rozciągania stali

można sporządzić tzw. wykres rozciągania w układzie miękkiej pokazuje rys.9.11.

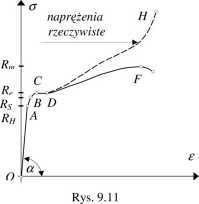
Na osi odciętych mamy odkształcenie liniowe włókien równoległych do osi pręta, wyznaczane ze wzoru Al

£ = -

gdzie: L₀ - pierwotna długość

odcinka próbki (długość pomiarowa), którego wydłużenia A! są rejestrowane.

Na osi rzędnych występują naprężenia normalne w przekroju poprzecznym pręta, wyznaczane ze wzoru:

N

a = —, gdzie: N - siła rozciągająca próbkę,

A

rejestrowaną podczas badania, Ao - pole pierwotnego przekroju poprzecznego próbki..

Ponieważ podczas wykonywania próby pole przekroju poprzecznego próbki maleje, to te naprężenia są wielkościami umownymi.

Omówimy krótko poszczególne charakterystyczne części wykresu rozciągania. Na prostoliniowym odcinku OA odkształcenia są liniowo zależne od naprężeń i znikają po zdjęciu obciążenia. Tak więc własności materiału są liniowo sprężyste i największe naprężenie, przy którym te własności jeszcze występują R_H, nazywamy granicą proporcjonalności albo granicą stosowania prawa Hooke’a. Na krzywoliniowym odcinku AB, kończącym się naprężeniem R_s , materiał jest jeszcze sprężysty ale zależność między naprężeniami i odkształceniami jest nieliniowa. R_s nazywamy granicą sprężystości, po jej przekroczeniu w materiale zaczynają występować trwałe (plastyczne) odkształcenia. W punkcie C wykresu, któremu odpowiadają naprężenia R_e, w próbce narastają znaczne odkształcenia: 10 do 15 razy większe niż przy granicy sprężystości, przy stałych a nawet malejących naprężeniach. Zjawisko to nazywamy płynięciem materiału (część CD określana jest jako platforma płynięcia), a naprężenie R_e - wyraźną granicą plastyczności. Płynięcie materiału kończy się w punkcie D, w którym zmienia się charakter wykresu. Przyrost odkształceń wymaga przyrostu naprężeń, materiał się wzmocnił i sytuacja taka trwa aż do punktu F, któremu odpowiada największa siła uzyskana w czasie próby. Naprężenia odpowiadające temu punktowi R_m, nazywamy wytrzymałością na rozciąganie. W momencie badania, któremu odpowiada na wykresie rozciągania punkt F, w próbce tworzy się przewężenie, tzw. szyjka i prawie natychmiast próbka w tym miejscu ulega zerwaniu.

Podczas próby rozciągania prócz wyznaczenia wyżej opisanych granicznych wartości naprężeń możemy wyznaczyć moduł Younga i liczbę Poissona. Moduł Younga to nic innego jak tangens kąta nachylenia liniowej części wykresu rozciągania:

„ o

E = — = tg a.

£

Rejestrując zmianę średnicy próbki Ad podczas próby możemy wyznaczyć odkształcenia liniowe w kierunku poprzecznym do osi pręta :

78