4037603094

Adam Bodnar: Wytrzymałość Materiałów. Osiowe rozciąganie i ściskanie

7 A, ->    \*-2A_t+4i+\ _u

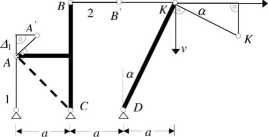
Położenia punktu A po deformacji poszukujemy na prostopadłej do pierwotnego kierunku

pręta 1 i prostopadłej do kierunku odcinka postępujemy w punkcie K.

Współrzędne przemieszczenia wektora punktu u_k=2A\+A2 i v_K = (2Ą + ^) tg a gdzie: tg a= 1/2.

Przykład 9.8.10. Pręt BC ( na odcinku BI - drewniany na odcinku 1C - stalowy), potrzymuje sztywną ramę AD konstrukcji prętowej o geometrii i obciążeniu jak na rys. Wyznaczyć wymiar a pręta BC z warunku nośności Jeśli: wytrzymałość obliczeniowa na rozciąganie stali R_s = 215 MPa, drewna R_d = 8 MPa, i warunku użytkowania żądającym aby pionowe przemieszczenie punktu D - vp nie przekraczało 1 cm. Moduł sprężystości wynoszą: stali E_s = 205 GPa, drewna E_d= 9 GPa.

Rozwiązanie

AC, który jest nieodkształcalny. Podobnie K wynoszą:

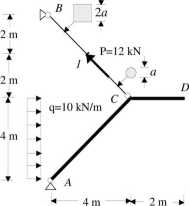
Obliczenie sił osiowych w pręcie BC.

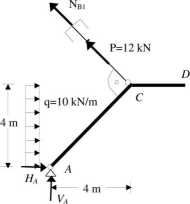
Siłę na odcinku BI wyznaczymy z warunku zerowania się momentów względem punktu A wszystkich sił działających na odciętą część konstrukcji (rys. obok)

Z^M„=⁰'

N_m*4j2 + 12*472-10*4* 2 = 0,

N_m =2.142 kN.

Siła na odcinku 1C jest równa:

N_IC =N_Bi+P = 2.142 +12.00 = 14.142 kN.

90