4037603089

Adam Bodnar: Wytrzymałość Materiałów. Osiowe rozciąganie i ściskanie

Rozwiązanie

Z warunku nośności wynika:

—<R_cm^> a >— --> a>--- -> a>33.3*10^_2m

s*a ■    s*R_cm    9*io~² *2*10⁶

r ^s~⁹ cm Przyjęto do wykonania a=35 cm.

W dwóch ostatnich powyższych przykładach warto zauważyć jak schemat obliczeniowy (pręt pryzmatyczny osiowo obciążony) daleko odbiega od rzeczywistej konstrukcji.

Przykład 9.8.5. Wyznaczyć nacisk N na 1 m długości przyczółka mostu jaki wywiera płyta żelbetowa o grubości h = 42 cm przy wzroście temperatury AT = 25° C jeśli moduł sprężystości podłużnej betonu E = 38.6 GPa a współczynnik rozszerzalności liniowej

a_T = 10‘⁵ /°C. Płyta przylega ściśle do obu przyczółków.

Rozwiązanie

Wydłużenie rozpiętości płyty / w przypadku jej swobodnego podparcia byłoby równe Al = a_T AT l.

Skrócenie jej rozpiętości na skutek przyłożenia ściskającej siły wynosi Al = Nl/EA. Porównanie obu tych wielkości daje równość:

a_TATI=—^NI -» N=a_T AT Eh=lO~⁵ *25*38.6*10⁹ *0.42=4.053*10³ kN.

^T E*h*1

Widać z powyższego, że ta siła (a jest ona bardzo duża) nie zależy od rozpiętości płyty mostowej. Oczywiście szerokość potrzebnej szczeliny dylatacyjnej będzie od niej zależała.

Przykład 9.8.6. Dobrać potrzebny przekrój pręta AB w pasie dolnym podanej stalowej kratownicy, jeśli wytrzymałość obliczeniowa stali R = 215 MPa. Przekrój pręta ma być złożony z dwóch kątowników równoramiennych. Po wyznaczeniu przekroju obliczyć nośność tego pręta.

100 kN 100 kN 100 kN 100 kN 100 kN

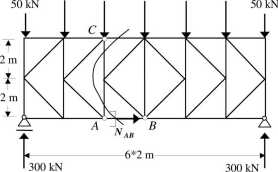
Rozwiązanie

Siłę w pręcie AB wyznaczymy metodą Rittera. Warunek równowagi odciętej lewej części kratownicy daje:

2;m£=0

300 * 4 - 50 * 4-100 * 2-*4=0 N_ab =200kN (pręt jest rozciągany)

86