4037603082

Adam Bodnar: Wytrzymałość Materiałów. Osiowe rozciąganie i ściskanie

9. OSIOWE ROZCIĄGANIE I ŚCISKANIE 9.1. Naprężenia i odkształcenia

Osiowe rozciąganie pręta pryzmatycznego występuje wówczas, gdy układ sił zewnętrznych po jednej stronie przekroju poprzecznego pręta redukuje się do wypadkowej prostopadłej do przekroju, zaczepionej w jego środku ciężkości i skierowanej zgodnie z normalną zewnętrzną. Wypadkową tę N nazywamy siłą osiową lub podłużną i w przypadku gdy jej zwrot jest zgodny ze zwrotem normalnej zewnętrznej nazywamy siłą rozciągającą a jej współrzędnej N przypisujemy znak dodatni. Naszym zadaniem będzie wyznaczenie elementów macierzy naprężeń i odkształceń w dowolnym punkcie pręta, bo te wielkości określają w nim stan naprężenia i odkształcenia oraz współrzędnych wektora przemieszczenia.

Rozważmy więc, pokazany na rys. 9.1 pręt pryzmatyczny o polu przekroju poprzecznego A, określony w układzie osi (X, Y ,Z), w którym oś X jest osią pręta, a osie (Y, Z) są osiami centralnymi jego przekroju poprzecznego. Pręt wykonany jest z izotropowego, jednorodnego, liniowo sprężystego materiału o stałych materiałowych E oraz V.

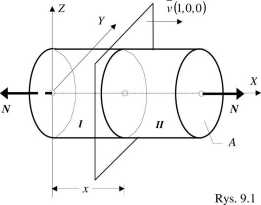
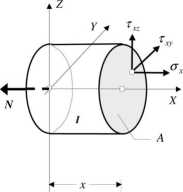
Dokonajmy myślowego przekroju pręta na dwie części, odrzućmy część II a do części I przyłóżmy układ sił wewnętrznych, który symbolicznie zaznaczymy przez jego miary tzn. naprężenia <r_v,    zaczepione w dowolnie wybranym punkcie przekroju poprzecznego.

Z twierdzenie o równoważności odpowiednich układów sił wewnętrznych i zewnętrznych wynika, że:

rs_t{w',) = s__t{z„} S_y{W,} = S_v{z,,}, s₌{iv,} = s_;{z„),

[M„ ,{w,}= M₀,{Z„}, M,y{w,}=    M_0l{w,} = M„_;{Z„},

rzuty sum i momentów zredukowanego układu sił wewnętrznych przyłożonych do części I oraz układu sił zewnętrznych przyłożonych do części II, są sobie równe.

Zgodnie z powyższym możemy w rozważanym przypadku napisać poniższe związki:

71