4037603096

Adam Bodnar: Wytrzymałość Materiałów. Osiowe rozciąganie i ściskanie

Podobnie możemy wyznaczyć zmiany wymiarów (zmniejszenie) przekroju poprzecznego pręta:

Nb    ., Nh

Ab--v-- oraz Ah=-v-.

EA    EA

Na końcu tej części naszych rozważań należy powiedzieć, że wyprowadzone zależności mogą być stosowane, w tej formie, zarówno dla przypadku rozciągania jak i ściskania osiowego.

W tym drugim przypadku wypadkowa N ma zwrot przeciwny do normalnej zewnętrznej, a jej współrzędnej N przypisujemy znak ujemny. Przy czym w przypadku ściskania, tj. gdy N<0 konieczne jest dodatkowe sprawdzenie czy pręt jest w stanie równowagi statecznej.

9.2. Analiza stanu naprężenia i odkształcenia

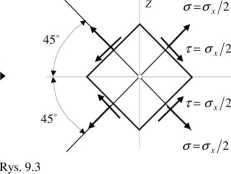
W analizowanym przypadku występuje jednoosiowy i jednorodny stan naprężenia scharakteryzowany jednym tylko naprężeniem normalnym w przekroju poprzecznym pręta, które jest równocześnie maksymalnym naprężeniem głównym w przypadku rozciągania (rys.9.3) i minimalnym w przypadku ściskania. Pozostałe dwa naprężenia główne są równe zeru a ich kierunki to jakiekolwiek dwa prostopadłe do siebie i równocześnie prostopadłe do osi pręta.    ^z

Ekstremalne naprężenia styczne występują w przekrojach nachylonych pod kątem 45 do osi pręta (rys. 9.3) i równają się połowie naprężeń normalnych w przekroju poprzecznym. Koło Mohra dla rozważanego przypadku pokazane jest na rys. 9.4.

a_v = (Tj/2

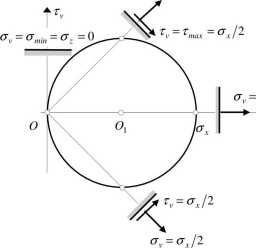
Rys. 9.4