4037603101

Adam Bodnar: Wytrzymałość Materiałów. Osiowe rozciąganie i ściskanie

, =-, gdzie : d₀ - pierwotna średnica próbki.

d„

Liczbę Poissona otrzymujemy dzieląc odkształceń liniowe w kierunku poprzecznym przez odkształcenia liniowe w kierunku równoległym do osi próbki:

Wyżej wspomniano, że naprężenia na wykresie rozciągania są naprężeniami umownymi, gdyż otrzymane zostały przez podzielenie siły rozciągającej przez początkowe pole przekroju poprzecznego. Naprężeniami rzeczywistymi nazywać będziemy iloraz siły przez aktualne pole powierzchni przekroju. W początkowym stadium próby rozciągania między tymi dwoma naprężeniami nie ma istotnych różnic, pojawiają się one dopiero pod koniec platformy płynięcia. Przebieg zmian naprężeń rzeczywistych na rys.9.11 pokazany został linią przerywaną.

Wykres rozciągania na rys. 9.11 pokazuje cechy i zachowanie się stali miękkiej nazywanej też stalą niskowęglową bo zawartość węgla w jej składzie nie przekracza 0.30 %. Stal o takiej charakterystyce jest powszechnie stosowana w budowlanych konstrukcjach stalowych.

Na rys. 9.12 naszkicowane zostały wykresy rozciągania innych metali.

Widoczny jest brak w pewnych materiałach

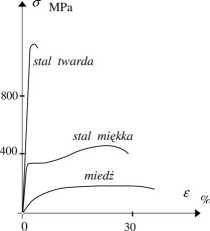
Rys. 9.12

wyraźnej granicy plastyczności R_e. W takich przypadkach posługujemy się umowną granicą plastyczności oznaczaną przez R₀ 2 i definiowaną jako naprężenie, przy którym trwałe odkształcenia liniowe wynoszą 0.2 %. W przypadku statycznej próby ściskania (sposób jej wykonania w przypadku metali można znaleźć w normie PN-57/H-04320) w zakresie naprężeń poniżej granicy plastyczności charakter wykresu ściskania w układzie o-e nie odbiega od wykresu rozciągania. Stal miękka, aluminium czy miedź mają granicę proporcjonalności, sprężystości i plastyczności nieomal identyczną jak przy rozciąganiu. Przy większych naprężeniach charakter wykresu się zmienia i jest to powodowane wpływem aktualnej geometrii badanej próbki - zwiększa się pole jej przekroju poprzecznego.

79