7696131551

5. UKŁADY RÓWNAŃ LINIOWYCH - STUDIA

A.    M. e t 9. d.a. w Y z n ą c z n i k a C ram e ra-u k ł a dy li ni o w ę

Metoda Craniera dotyczy głównie układów kranierowskieh (tzn. układów posiadających u równań pierwszego stopnia on niewiadomych), w których macierz A współczynników przy niewiadomych jest kwadratowa (tzn. posiada jednakową ilość wierszy i kolumn) oraz det A * 0.

anxi + a12x2 + ••• + alnxn = b2	^ail ^ai2 ”* ^ain		*1-		\bi-l
a21x1 + a22x2+- + a2nxn = b2 0	^a21 ^a22 ^a2 n	•	*2	=	b2
^anl^xl + ^an2^x2 + - + ^ann^xn = K	Clni CLn2 ®7in.		•*n-		■ bn -

Postać macierzowa powyższego układu równali liniowych:    a x = B

A «=> macierz, współczynników przy niewiadomych:

X •=> macierz. (wektor) niewiadomych:

^au	^al2	^aln			'V			' V
^a21	^a22	^a2 n		x„ = x =	*2		B =	^b2
^anl	^an2	•” ^ann	nxn		_^Xn_			A.

B ■=> macierz, (wektor ) wyrazów wolnych.

A =

A ■ X = B *

d^t b

X = A-¹ B = r-r d^t • b = . .

A    A

dla |A| * 0

w,

Twierdzenie Cramera:    X; = —

¹ w

IAI    f|A|*0

- dla <

|A|    U =1.2 n

Rozwiązanie

układu:

r =^1

^Xl _W

*2

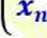
Wz

W

W

	^ali	^al2
gdzie: W = |A| =	^a21	^a22	^a2 n
	^anl	^a*2	^ann

oraz

	b t	^a12 •	’ ^aln		^an	b i	"■ ^aln		^all	^al2	- b i
II <T	b2	^a22	^a2n	, w2 =	^a2l	b2	^a2n	W = , ..., vv„	^a21	^a22	- b2
	K	^an2 •	^ann		^anl	K	^ann		^anl	^an2	bn

Analiza rozwiązali:

1)    W*0

2)    W = W, = ... = W„ = «

3)    \V = 0 i istnieje Wj & 0

<J=t> istnieje jedno rozwiązanie {układ oznaczony) nieskończenie wiele lub brak rozwiązań {układ nieoznaczony lub sprzeczny)

<o> l)rak rozwi ązań {układ sprzeczny)

Jeżeli wszystkie wyrazy wolne bi = 0. to układ jest jednorodny, jeżeli choć jedno bi 0. to układ jest niejednorodny. Układ jednorodny jest układem zgodnym (zawsze ma rozwiązanie zerowe oraz. może mieć również rozwiązania niezerowe).

Analiza rozwiązań układu jednorodnego (tzn. gdy bi = 0):

1)    W *0    jedno rozwiązanie trywialne (zerowe) postaci: Xj =xy = ... = x„ = 0

2)    W = 0    <o> j.w. + istnieje też rozwiązanie nietrywialnie (niezerowe)

© Copyright by Ewa Kędziorczyk    -16-

w w w. ma tematyka. sosu o wiec.p I