18783

Pochodne cząstkowe funkcji dwóch zmiennych

Ekstrema lokalne funkcji dwóch zmiennych

Twierdzenie (warunek konieczny):

Jeżeli f{x,y) ma w punkcie (x₀,y₀)e D ekstremum lokalne i istnieją w tym punkcie pochodne cząstkowe rzędu pierwszego, to:

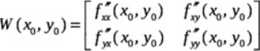
f,'(Wo) = ° fy(x_o,y_o) = 0

Twierdzenie (warunek wystarczający):

Jeżeli f(x,y) ma pochodne cząstkowe rzędu pierwszego i drugiego ciągłe w otoczeniu

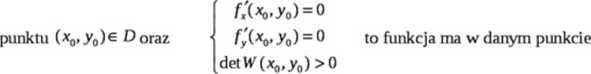
ekstremum lokalne.

1)    Jest to maksimum lokalne, jeżeli f* (x, y) < 0

2)    Jest to minimum lokalne, jeżeli f'_x (x, y) > 0

Jeżeli det lV(x₀,y₀) < 0 _f to w punkcie (*₀»    ^ nie ¹¹¹³ ekstremum, natomiast

det W(x,j,^o) = 0 nie rozstrzyga o istnieniu ekstremum.

Ekstrema Funkcji dwóch zmiennych

G(x₀,y₀) = ^+y₀= 0 G(x₀, y₀) = x₀ xy₀ ⁼ 0 Funkcja ma w punkcie (x₀,y₀):

Maksimum warunkowe, gdy:

BS(Xo,y₀)c:D V(x,y)e S(x₀,y₀)f(x₀,y₀) > f(x,y) oraz G(x_o,y_o) = 0 Minimum warunkowe, gdy:

3S(x₀,y₀)czD V(x,y)e S(x_Q,y₀)f(x₀,y₀) < f(x,y) oraz G(x_o,y₀) = 0