CCF20090319040

Pochodne cząstkowe i różniczki 49

Zadania

Obliczyć pochodne cząstkowe względem każdej zmiennej występującej w danej funkcji

1.	u = xlny - e^Xy/y,	2.	u = xy^2z^4 — x sin y,
3.	X u = — + yVx, Vv	4.	z = y/x^2 + y^2 - 3xy,
5.	£ II h" N	6.	u = y^3e^x2+y,
7.	Z = ln(z + lny),	8.	z = y sin^2 x.

9. Wykazać, że w równaniu Clapeyrona pv — RT, gdzie p oznacza ciśnienie, V - objętość, T - temperaturę w skali Kelwina, R - stałą gazową, iloczyn pochodnych cząstkowych ma własność

dp dv dT _ dv dT dp

10. Zbadać szybkość zmian objętości stożka V:

a)    przy zmianie promienia podstawy r,

b)    przy zmianie wysokości h.

Różniczką funkcji y = f(x) nazywamy iloczyn pochodnej tej funkcji przez dowolny przyrost dx zmiennej niezależnej i oznaczamy symbolem dy (od łac. differentia = różnica)

dy = df(x) = f\x)dx.    (2.24)

Różniczkę funkcji można zinterpretować w następujący sposób. Niech krzywa na rysunku 23 przedstawia wykres funkcji y = f(x). Poprowadźmy styczną AC do wykresu w punkcie A. Z trój

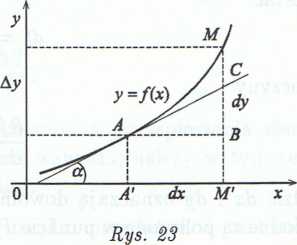
kąta ABC otrzymamy BC = AB-tg a. Ale AB = Ax = dx, tg a równa się pochodnej y' w punkcie A, więc BC = = y'dx = dy. Różniczka przedstawia zatem główną część przyrostu funkcji Ay = BM\ jest więc wartością przybliżoną przyrostu funkcji Ay. Przybliżenie to jest tym lepsze, im mniejsza jest wartość dx.