102790

Miolechnołogia I seni. M .Twardowska Równania różniczkowe 1 rzędu. 1

Równania różniczkowe rzędu pierwszego

J9(v) dy = Jf(x)dx + C

• Równanie o zmiennych rozdzielonych:

dy f(x)

— — -. Rozwiązaniem jest

dx g(y)

Równanie jednorodne (względem x i y) :    = f (- \ . Równanie to można za pomocą podstaw

om \£/

ienia u(x) = — sprowadzić do równania o zmiennych rozdzielonych (wtedy y = ux. y' = u'x + u).

Równanie różniczkowe liniowe rzedli pierwszego: ^ = p(x)y + q(x). Rozwiązujemy najpierw równanie

dx

liniowe jednorodne czyli —^ -f p(x)y — 0 jest to równanie o zmiennych rozdzielonych. Rozwiązanie

dx

otrzymujemy w postaci y(x) =    = Cyi(x), z pewną ustaloną funkcją yi(x). Następnie

uzinienniamy stalą C, tzn. zakładamy, że rozwiązaniem równania niejednorodnego jest funkcja postaci: y(x) = C(x)yj(x), z pewną nową funkcją niewiadomą C(x). Podstawiamy y(x) do rozwiązywanego równania i znajdujemy funkcję C(x).

• Równanie różniczkowe Bernoulliego:

dy

dr

= P{x)y + ę(x)y°

(gdzie o ^ 0.1. 1)0 dla a = O mamy

równanie liniowe, a dla a = 1 równanie o zmiennych rozdzielonych.) Za pomocą podstawienia z(x) = y^1-° sprowadzamy to równanie do równania liniowego.

g) y’ - 9x¹y = 3(x² - x²)y$

1. Rozwiązać równania o zmiennych rozdzielonych:

a) ^ = e^2*+» dx	b) xi/ + y = V^2	c) 2x^/1 - y^2dx + ydy = 0
d)J-^J(»+l)^1 3dx = (l + x)Vc/j/	\ ^dy 2. e)-=xy^2 + x	f) (y^1 + xy^2)dx + (x^1 - x^2y)dy = 0
2. Rozwiązać równania jednorodne	względem x i y:
aj dy _ x^2 + y^1' dx xy	b) dy x + y ' dx 3x - y	c) y^2 + x^1y' = myj/
d)(y^2 - 3x^1)dy + 2\xydx = 0	e) y' - xy' = x + yy'	f) (x^2 + 2xy - y^1) + (y^2 + 2xy - x^1)tf = 0

c) \f + 2xy = e”*² f) y' - e^xy = e²*

v dy , 2    x

^C) dx 3^U    y/ii

d)

dy , v

dx x

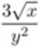
e)

y/y

+ 4x_v/y = 2xe

.2

f) y' - 9x¹y = (x² + x²)y§

1

Rozwiązać równania liniowe:

a) ^ - y tgx = 2sinx    b) »/ + - = x²

dx    x

d) y' — 2xy — 2x¹    e) y' + ycosx = sin xcosx

g)*/*¹ ₂^2j»/=l, y(l) = l+e x^Ł

2

a) xy' + xy² - y = O    b) y' + xy = xy“¹

3

Rozwiązać równania Bernoulliego: