W5. Algorytmy wyznaczania najkrótszej ścieżki w digrafie.

Liczne zagadnienia optymalizacji są matematycznie równoważne znajdowaniu najkrótszej ścieżki w pewnym grafie. Z tego powodu algorytmami wyznaczania najkrótszych ścieżek zajmowano się poważniej niż jakimikolwiek innymi algorytmami w teorii grafów. Opublikowano setki prac na ten temat i zaproponowano dziesiątki algorytmów oraz ich modyfikacje. Niektóre z tych algorytmów są lepsze niż inne, niektóre nadają się do grafów o szczególnej strukturze, a niektóre są nieznacznymi modyfikacjami algorytmów wcześniejszych.

Istnieją różne typy problemów wyznaczenia najkrótszej ścieżki. Do najczęściej spotykanych problemów zaliczymy:

1. Najkrótszą ścieżkę między dwoma określonymi wierzchołkami.

2. Najkrótsze ścieżki między wszystkimi parami wierzchołków.

3. Najkrótsze ścieżki od określonego wierzchołka do wszystkich innych wierzchołków.

4. Najkrótszą ścieżkę między określonymi wierzchołkami, która przez nie przechodzi.

5. Druga, trzecia itd. z kolei najkrótsza ścieżka.

Do powyżej przedstawionej klasyfikacji typów dodamy jeszcze modyfikowaną czwartą, a mianowicie szukanie najkrótszej ścieżki między określonymi wierzchołkami, która przez nie przechodzi. Właśnie do tego typu zadania należy nasz projekt z matematyki dyskretnej.

W wykładzie tym będziemy rozważać digrafy G = <V, E> o łukach z wagami. Oznacza to, że każdemu łukowi (u, v) ∈ E jest przyporządkowana pewna liczba rzeczywista w(u, v) zwaną wagą tego łuku. Przyjmujemy dodatkowo, że w(u, v) = ∞, jeśli nie ma łuku skierowanego od wierzchołka u do wierzchołka v. Jeśli ciąg

v₁, v₂, ... , v_p,

określa drogę w G, to jej długość definiujemy jako

.

Przyjmując w dowolnym grafie wagę każdej krawędzi równą jedności, otrzymujemy zwykłą definicję długości drogi w sensie liczby krawędzi. Długość drogi wynosi 0 dla p=0.

Interesować nas będzie znalezienie najkrótszej drogi między ustalonymi wierzchołkami s, t ∈ V.

Można przytoczyć wiele interpretacji praktycznych problemu najkrótszych dróg. Wierzchołki mogą odpowiadać na przykład miastom, zaś każdy łuk pewnej drodze, której długość podana jest przez wagę tej krawędzi. Szukamy wtedy najkrótszego połączenia między miastami. Waga krawędzi może też odpowiadać kosztowi lub czasowi przesłania informacji między wierzchołkami. W takim przypadku szukamy najtańszej lub najszybszej drogi przesłania informacji. Jeszcze inną sytuację otrzymujemy, gdy waga łuku (u, v) jest równa prawdopodobieństwu p(u, v), bezawaryjnej pracy kanału przesyłania informacji. Jeśli założymy, że awarie kanałów są od siebie niezależne, to prawdopodobieństwo sprawności drogi przesyłania informacji jest równe iloczynowi prawdopodobieństw odpowiadających jej łuków. Problem znajdowania najbardziej niezawodnej drogi można łatwo sprowadzić do zagadnienia najkrótszych dróg poprzez zamianę wag w(u, v) na -log p(u,v).

Algorytmy najkrótszych ścieżek mogą mieć zastosowanie w metodzie planowania przedsięwzięć zwanej PERT (Project Evaluation and Review Technique) lub CPM (Critical PathMethod). Metoda ta polega na skonstruowaniu grafu (tzw. sieci PERT lub sieci CPM), którego łuki odpowiadają pewnym elementarnym zadaniom z których składa się przedsięwzięcie, a ich wagi wskazują na czas potrzebny na wykonanie poszczególnych zadań. Zakładamy ponadto, że dla dowolnych łuków (u,v), (v,t) tego digrafu, zadanie reprezentowane przez (u,v) musi być zakończone przed rozpoczęciem zadania reprezentowanego przez (v,t). Łatwo zauważyć, że taki digraf musi być acykliczny, tzn. nie może zawierać cykli. Naszym zadaniem jest znalezienie najdłuższej drogi z wierzchołka s, odpowiadającego rozpoczęciu przedsięwzięcia, do wierzchołka t odpowiadającego jego zakończeniu. Drogę taką nazywamy ścieżką krytyczną. Jej długość określona jest przez czas potrzebny na wykonanie całego przedsięwzięcia. Oczywiście zagadnienie to sprowadza się do problemu najkrótszej drogi poprzez zamianę znaku każdej wagi w(u,v).

Algorytm Forda-Bellmana.

Na początku podamy algorytm dla ogólnego przypadku znajdowania odległości od źródła w wierzchołku s do wszystkich pozostałych wierzchołków. Zakładamy jedynie brak cykli o ujemnej długości. Z algorytmem tym wiążą się zwykle nazwiska L. Forda i R. Bellmana ([3, str.108])

Dane: Digraf elementarny <V, E> o n wierzchołkach z wyróżnionym źródłem s , macierz wag krawędzi W[u,v],u,v∈V. Digraf nie zawiera cykli ujemnych długości.

Wyniki: Odległości od źródła do wszystkich wierzchołków digrafu: D[v] = d(s,v).

• Begin

• for v∈V do D[v]:=W[s,v]; D[s]:=0;

• for k:=1 to n-2 do

• for v∈V \ {s} do

• for u ∈ V do
  D[v] := min(D[v], D[u] + W[u,v]

• End

Oczywiste jest, że złożoność czasowa algorytmu wynosi O(n³). Obliczenia możemy zakończyć dla k < n-2, gdy wykonanie pętli 4 nie powoduje zmiany żadnej spośród zmiennych D[v]. Jednak taka modyfikacja algorytmu nie zmienia w istotny sposób jego złożoności. W przypadku grafów rzadkich (m << n²) wygodnie jest reprezentować graf poprzez listy incydencji. Wtedy otrzymujemy algorytm
o złożoności O(nm).

Algorytm Dijkstry.

Wśród kilku algorytmów, które zostały zaproponowane dla wyznaczania najkrótszej ścieżki między określoną parą wierzchołków, być może najbardziej efektywnym jest algorytm pochodzący od Dijkstry. W algorytmie tym wszystkie wierzchołki digrafu podzielone są na dwie grupy: tymczasowe oraz stałe, które nazwiemy eliminowanymi. Algorytm rozpoczyna działanie przypisując wartość 0 dla wierzchołka początkowego s, który jest pierwszym wierzchołkiem eliminowanym. (Poprzez wartość wierzchołka i będziemy rozumieć wartość drogi od wierzchołka s do wierzchołka i.) Pozostałe n-1 wierzchołków otrzymują wartość ∞. Następnie,
w każdej iteracji inny wierzchołek otrzymuje status eliminowanego zgodnie
z następującymi zasadami:

1. Każdy wierzchołek j, który nie należy do eliminowanych, otrzymuje nową wartość tymczasową, która jest mniejszą z dwóch liczb: „stara” wartość łuku od wierzchołka s do wierzchołka j i „nowa” wartość jako suma wartości pary łuków: (s,i) i (i,j), gdzie i jest ostatnim eliminowanym wierzchołkiem,

2. Jeśli znajduje się wierzchołek z najmniejszą wartością wśród wszystkich wierzchołków j, tzn. incydentnych do ostatniego eliminowanego wierzchołka i, to ten „najmniejszy” będzie należeć do eliminowanych i otrzymuje indeks i.

Kroki 1 i 2 powtarza się na przemian, aż końcowy wierzchołek t otrzyma status eliminowanego. Pierwszy wierzchołek po wierzchołku s, któremu należy przypisać status eliminowanego, jest wierzchołkiem najbliższym wierzchołkowi s.
Z pozostałych n-2 wierzchołków następnym, który będzie eliminowany, jest drugi z kolej najbliższy od wierzchołka s, itd. Łatwo udowodnić na podstawie indukcji matematycznej, że wartość każdego eliminowanego wierzchołka jest najkrótszą odległością od wierzchołka s. Na rys. 5-2 pokazany został przykład kolejności eliminacji wierzchołków wg algorytmu Dijkstry.

Opisany algorytm nie podaje właściwie najkrótszej ścieżki od wierzchołka startowego do wierzchołka końcowego, daje on tylko najkrótszą długość. Najkrótszą ścieżkę można łatwo skonstruować poruszając się wstecz od wierzchołka końcowego tak, że idzie się do tego poprzednika, którego wartość różni się dokładnie o długość łuku łączącego. Wadą podobnego algorytmu wyznaczenia najkrótszej ścieżki jest obecność kilku wierzchołków o takiej samej wartości. Alternatywnie można zaproponować prostszy algorytm, oparty na dodawaniu nazwisk łuków w toku redukcji kolejnego wierzchołka i.

Jeżeli w tym algorytmie przepisywalibyśmy status eliminowanych dalej, aż do chwili gdy każdy wierzchołek oprócz źródłowego i końcowego będzie eliminowany, to otrzymalibyśmy algorytm wyznaczania najkrótszej ścieżki od wierzchołka źródłowego do wszystkich innych wierzchołków.

Poniżej zamieszczono opis algorytmu Dijkstry w uproszczonej wersji języka Pascal [3].

Dane: Digraf elementarny <V, E> o n wierzchołkach z wyróżnionym źródłem s , macierz wag krawędzi W[u,v],u,v∈V. Digraf bez ujemnych łuków lub acykliczny.

Wyniki: Odległości od źródła do wszystkich wierzchołków digrafu: D[v] = d(s,v).

• Begin

• for v∈V do D[v]:=W[s,v]; D[s]:=0;

• T∈V \ {s};

• While T≠∅ do

• begin

• u:=dowolny wierzchołek r∈T taki, że

• D[r]:= min {D[p], p∈T};

• T:=T \ {u};

• for v∈T do D[v]:= min(D[v], D[u]+W[u,v]);

• end

• End([3], str.110)

Jeżeli weźmiemy najkrótszą ścieżkę od wierzchołka startowego do każdego innego, to suma mnogościowa tych ścieżek będzie didrzewem o korzeniu w wierzchołku startowym. Takie drzewo nazywa się najkrótszym rozgałęzieniem lub najkrótszym didrzewem. Czas obliczeń algorytmu Dijkstry jest proporcjonalny do n². Przy znajdowaniu odległości między wszystkimi parami wierzchołków algorytm Dijkstry należy powtarzać n razy. Wtedy czas obliczeń tego typu zadania wg algorytmu Dijkstry jest proporcjonalny do n³.

[Lipski, 109-111; Deo, 379-385]

Algorytm Warshalla-Floyda.

Wśród algorytmów wyłącznie przeznaczonych do znajdowaniu odległości między wszystkimi parami wierzchołków znany jest algorytm Warshalla-Floyda. Algorytm ten jest prostszy od algorytmu Dijkstry i zawiera trzy pętle w pętli.

Dane: Digraf elementarny <V, E>. Digraf nie zawiera cykli ujemnych długości.

Wyniki: Odległości między wszystkimi parami wierzchołków: D[i, j] = d(v_i,v_j).

• Begin

• for i:=1 to n do

• for j:=1 to n do D[i, j] := W[i, j];

• for i:=1 to n do D[i, j] := ∞; ( 0 = ? )

• for k:= 1 to n do

• for i:= 1 to n do

• for j :=1 to n do

• D[i, j]:= min(D[i, j], D[i, k]+D[k,j];

• End

Algorytm działa na zasadzie wstawiania jednego lub więcej wierzchołków do drogi jeśli tylko jest to korzystne. Dzięki wykorzystaniu trzech pętli w pętli, czas obliczania algorytmu jest proporcjonalny do n³. Podany algorytm nie podaje ścieżki, a tylko najkrótsze odległości. Otrzymanie ścieżki jest nieco bardziej skomplikowane niż w algorytmie Dijkstry, ponieważ teraz trzeba analizować n(n-1) ścieżek, a nie tylko jedną. Efektywna metoda uzyskania wierzchołków pośrednich polega na wykorzystaniu macierzy optymalnych strategii. Na rys. 5-3 pokazany został prostszy sposób wyznaczania macierzy minimalnych odległości, bazowany na równoległym do dodawania wartości łuków połączeniu ich tras (wiersz 12).

Algorytm redukcji

W niektórych zadaniach (np. przy obliczeniu minimalnych odległości między określonymi wierzchołkami digrafu) skuteczny jest algorytm redukcji. Treść tego algorytmu zaprezentowana była w poprzednich wykładach. Dla uproszczenia wspomniane określone wierzchołki nazwiemy terminalnymi. Teraz zadanie to można określić jako szukanie minimalnych odległości tylko między parami terminalnych wierzchołków, których ilość musi być mniejsza od ogólnej ilości wierzchołków digrafu.

Digrafy o ujemnych łukach i cyklach

Szukanie najkrótszych ścieżek w digrafie z ujemnymi łukami wymaga dodatkowych wyjaśnień. Jednym z praktycznych przykładów ujemnych łuków może być możliwość zmniejszenia kosztów przejazdu dzięki przewiezieniu jakiegoś obcego (w stosunku do firmy macierzystej) bagażu lub pasażerów. W takim przypadku do ogólnego kosztu przejazdu dodajemy ujemną liczbę, co oznacza zmniejszenie wartości drogi. Jeśli każdy cykl digrafu ma dodatnią długość, to najkrótsza droga jest zawsze drogą elementarną, tzn. nie ma powtórzeń w ciągu numerów wierzchołków drogi. Z drugiej strony, jeśli istnieje w digrafie cykl ujemnej długości, to odległość pomiędzy niektórymi parami wierzchołków jest nieokreślona, gdyż obchodząc ten cykl dostateczną liczbę razy możemy wskazać drogę pomiędzy tymi wierzchołkami o długości mniejszej od dowolnej liczby rzeczywistej. W takim przypadku można spytać o długość najkrótszej drogi elementarnej, jednak tak postawiony problem jest prawdopodobnie znacznie trudniejszy, gdyż między innymi zawiera w sobie zagadnienie cyklu Hamiltona.

Ciekawe, że w przypadku ujemnych łuków algorytm Dijkstry jest zupełnie bezradny. Przyczyną niedziałania algorytmu w takim przypadku jest fakt, że jeżeli tylko pewien wierzchołek zostanie eliminowany, to jego wartości nie można już zmienić po ujawnieniu łuku o ujemnej wadze. Można modyfikować algorytm Dijkstry kosztem rozsądnego ograniczenia ilości oraz wartości ujemnych łuków. Wtedy czas pracy algorytmu dla wszystkich wierzchołków będzie proporcjonalny do n⁴, a nie do n³.

Wstępne badania zachowania algorytmu redukcji przy obecności w digrafie łuków ujemnych oraz cykli o ujemnej długości ujawniły, że wartości minimalnych odległości zależą od kolejności redukowania wierzchołków, zaś wartość przejazdu wg obwodu Hamiltona nie zależy od kolejności redukowania wierzchołków. Szersze badania osobliwości szukania minimalnych odległości oraz optymalnych przejazdów wzdłuż obwodu Hamiltona, przy obecności w digrafie ujemnych łuków i cykli, wychodzi poza ramy niniejszych wykładów.

Porównanie właściwości algorytmów

Na rys. 5-1 przedstawiono tablice ograniczonych badań własności kombinatorycznych czterech algorytmów na przykładzie digrafu osiedla z Projektu-zero (Rys. p-2). Ten rzadki digraf zawiera 31 wierzchołków, 55 łuków i ma sześć terminalnych wierzchołków z obwodnicami. Specjalne liczniki w programach zliczały ilość niezerowych par łuków przy redukcji wierzchołków (Lij) oraz ilość zamian „starego” łuku na „nowy” lub zapisu nowego łuku przy nieobecności starego łuku (Lzn). Z tablicy łatwo wnioskować, że najgorsze wyniki w danym zadaniu i digrafie ma zastosowanie algorytmu Warshalla-Floyda. Prawie jednakowe dane w algorytmie Dijkstry i redukcji dotyczą eksperymentów z wariantem programu redukcji, zawierającym szukanie jego optymalnego wierzchołka. Zauważmy, że optymalna kolejność eliminowania wierzchołków jest „wrodzoną” własnością algorytmu Dijkstry. Algorytmiczną przewagą metody Dijkstry jest szybkie poruszanie się od źródła do końcowego wierzchołka przy eliminacji kolejnych wierzchołków, co istotnie redukuje czas szukania. Przy stosunkowym zwiększeniu ilości wierzchołków terminalnych szybsza jest metoda redukcji, ponieważ w metodzie Dijkstry rośnie współczynnik n(n-1). Również przy zbliżeniu badanego digrafu do pełnego, rośnie przewaga metody redukcji nad metodą Dijkstry.

Zasadniczym czynnikiem większych strat czasu w dwóch pozostałych algorytmach jest brak eliminacji wierzchołków po ich kolejnej redukcji.

Ciekawe jest, że metoda redukcji pozwala klasyfikować wszystkie podane metody szukania ścieżek z jednego punktu widzenia. Dla określenia własności każdej metody wystarczy wykorzystać trzy następujące definicje:

• Redukcja pełna - to proces szukania wszystkich możliwych par łuków, obliczenia ich sumy oraz zapisu nowego łuku lub zamianę starego,

• Redukcja jednokierunkowa - redukcja pełna z jednym tylko wchodzącym łukiem (pozostałą resztę wchodzących łuków ignorujemy).

• Eliminacja wierzchołka k - usuwanie wierzchołka k razem z incydentnymi łukami.

Znając wyżej wymienione definicje, możemy scharakteryzować każdą z czterech metod w następujący sposób:

• Algorytm Forda-Bellmana - redukcja jednokierunkowa bez eliminacji wierzchołków,

• Algorytm Dijkstry - redukcja jednokierunkowa z eliminacją wierzchołków,

• Algorytm Warshalla-Floida - redukcja pełna bez eliminacji wierzchołków,

• Algorytm redukcji - redukcja pełna z eliminacją wierzchołków.

Kończąc temat porównania własności algorytmów zaznaczmy, że nie należy spieszyć się z ogłaszaniem tego lub innego algorytmu jako przestarzałego lub nieskutecznego. Skuteczność algorytmu zależy od typu zadania, struktury rzadkiego grafu oraz sposobu kodowania danych. Oczywiście, wybieranie odpowiedniego algorytmu wymaga żmudnej pracy naukowo-badawczej.

Modyfikacje algorytmów szukania ścieżek. Dekompozycja

Jeśli graf jest rzadki, tzn. stosunek m/n² < 0.3, to można w taki sposób modyfikować algorytmy pokazane na rys. 5-1, aby uzyskać oszczędności tak pamięci jak - co jest najważniejsze - czasu procesorowego ich wykonania. Jeden z prostszych sposobów zaoszczędzenia czasu wykonania polega na użyciu operatora typu if W[i, j]=∞ then continue dla uniknięcia zbędnej pracy z nieistniejącymi łukami lub tymi, które nie tworzą pary (rys. 5-3). Bardziej wyrafinowany sposób polega na szczelnym kodowaniu łuków, np. tak, jak pokazano na rys.2-2. Dzięki takiemu kodowaniu udaje się szybciej odzyskać niezerową parę łuków. Kolejny sposób przyspieszenia obliczeń bazowany jest na szukaniu optymalnego wierzchołka redukcji tzn. takiego, który zabezpiecza minimum zapisu do tablicy wag.

Istotne oszczędności można uzyskać wykorzystując dekompozycję digrafu. Otrzymuje się wtedy najkrótsze ścieżki w każdym podgrafie i składa się je, aby otrzymać najkrótszą ścieżkę w całym grafie. Jako krańcowy przykład rozpatrzymy przypadek, w którym graf skierowany o n wierzchołkach składa się z dwóch digrafów o n/2 wierzchołkach każdy. Liczba obliczeń zmniejsza się z n³ do 2(n/2)³, a więc o 75%.

System kierowania ruchem drogowym firmy i miasta

Wyżej opisane algorytmy można zastosować do rozwiązywania niektórych zagadnień transportowych i drogowych. Jako przykład zastosowania algorytmów szukania minimalnych ścieżek, rozpatrzymy zadanie o projektowaniu oraz operatywnym kierowaniu procesem dostawy wyrobów z hurtowni do sklepów. Może to być, na przykład, zadanie związane z najtańszym kosztem przewozu produkcji piekarni do sieci sklepów spożywczych.

Przy rozwiązywaniu tego typu problemów początkiem musi być opracowanie danych wejściowych dla algorytmów czyli grafów. Rozpoczynamy
od przygotowania mapy osiedla, miasta, województwa itp., zależnie od zadania.
W przypadku zadania przewozu pieczywa będzie to mapa osiedla lub miasta. Określamy kierunek jazdy dla wszystkich ulic. Piekarnia oraz każdy ze sklepów muszą mieć na mapie osobno zaznaczoną drogę wyjazdową i wjazdową, nawet jeśli w rzeczywistości znajduje się ona obok prostej drogi (nazwiemy ją obwodnicą).

Podamy niektóre uwagi dotyczące przedstawienia mapy drogowej w postacie grafu. Umówimy się, że w ogólnym przypadku termin "graf" może oznaczać tak graf skierowany, jak i nieskierowany. Oznacza to, że dla konkretnych sytuacji i algorytmów nie jest istotne, czy graf jest skierowany, czy nie. Terminu "digraf" używamy w tym przypadku kiedy ważnym jest obecność w grafie przynajmniej jednego łuku i dla tego zastosowanie algorytmów opartych na grafach nieskierowanych nie mają sensu. Również używamy terminu "graf skierowany" kiedy chcemy podkreślić, że badany graf może zawierać tylko krawędzie. Zdanie "adekwatność grafu i mapy osiedla" będzie oznaczać, że graf mapy jest zgodny z mapą drogową, innymi słowy -że graf odpowiada mapie. Założymy, że graf mapy osiedla jest prosty, tzn. nie zawiera łuków (krawędzi) równoległych oraz pętli.

Dla opracowania algorytmu rozwiązywania zagadnienia komiwojażera niezbędnym jest przejście od mapy drogowej osiedla lub większego obszaru do grafu. W przypadku np. analizy mapy osiedla z piekarnią lub hurtownią i sklepami koniecznym jest użycie grafu skierowanego(digrafu).

Przyjmujemy, że digraf osiedla składa się z trzech typów elementów

-łuki, modelujące odcinki dróg,

-terminalne wierzchołki, modelujące piekarnią i sklepy,

-reszta wierzchołków, modelujących skrzyżowania.

Założymy, że piekarnia lub hurtownia odpowiada korzeniowi digrafu.

Modelowanie skrzyżowań. Skrzyżowaniem nazwiemy miejsce na mapie drogowej gdzie teoretycznie lub praktycznie ma sens ustawienie świateł drogowych. Jest to, np. miejsce połączenia trzech lub więcej dróg itp. Przy rysowaniu digrafu skrzyżowania obowiązuje zasada tożsamości dozwolonych ruchów oraz kosztów przejazdu pomiędzy wszystkimi sąsiadującymi skrzyżowaniami, innymi słowy jest to zasada bezmandatowego przejazdu. Na rys. 5-4a pokazano kilka przykładów „grafowania” skrzyżowań.

Szacujemy koszty przejazdu przez każdy odcinek ulicy, od skrzyżowania do skrzyżowania. Przy obliczaniu kosztów należy brać pod uwagę jak najwięcej czynników. Do podstawowych uwarunkowań obliczania kosztu przejazdu zaliczymy: długość odcinka ulicy, ilość jednokierunkowych pasów ruchu, położenie ulicy - czy
w centrum, czy na peryferiach, jakość nawierzchni (dziury w asfalcie źle wpływają na zawieszenie samochodu co pociąga za sobą częstsze remonty i wymianę części) oraz średnie natężenie ruchu. W systemie ciągłego monitoringu można posłużyć się gromadzonymi statystykami ruchu pojazdów i zmieniać koszty, np. zależnie od pory dnia i roku. Mapa może zostać przygotowana w formie elektronicznej i może być poddana obróbce przez preprocesor, który automatycznie wygeneruje graf w postaci gotowej do analizy przez algorytmy. Jeśli zadanie wykonujemy jednorazowo, to graf i jego komputerową reprezentację możemy przygotować ręcznie na papierze.

Następny krok polega na znalezieniu najtańszych tras przejazdu od piekarni do każdego ze sklepów i odległości od pozostałych sklepów. Do tego celu wykorzystujemy jeden z podanych wcześniej algorytmów, np. Dijkstry, Warshalla-Floyda, lub redukcji wierzchołków. Po otrzymaniu tych tras możemy zbudować graf pełny, w którym wierzchołkami są piekarnia i sklepy. Najtańszą trasę do rozwiezienia pieczywa znajdziemy stosując algorytm szukania ścieżki Hamiltona do tego grafu pełnego.

Na podobnej zasadzie działania opierają się nowoczesne systemy monitorowania ciężarówek, śmieciarek, itp. Kontroler ruchu (operator+komputer) otrzymuje aktualne wiadomości o stanie dróg, np. od obserwatorów w helikopterach, przez radio, lub z kamer wizyjnych itp. Na bieżąco uaktualniane są koszty przejazdu w miejscach występowania korków ulicznych, robót drogowych, zamkniętych ulicach itd. Poprzez system komunikacji radiowej kierowca otrzymuje optymalną trasę przejazdu łącznie z prawdopodobnymi problemami mogącymi na niej wystąpić. Samochód transportowy jest wyposażony również w system kontroli ruchu - komputer z monitorem, na którym jest pokazana trasa przejazdu i aktualne położenie samochodu na mapie.

Obwody Hamiltona. Generowanie obwodów Hamiltona

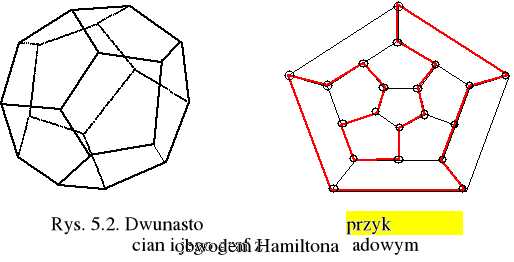
Historia słynnej zagadki-łamigłówki o wędrowaniu pomiędzy ustalonymi punktami bez powtórnego ich odwiedzania, powiązana jest z irlandzkim astronomem i matematykiem W. Hamiltonem (1805-1865). W roku 1859 wynalazł on pewną łamigłówkę i sprzedał ją producentowi gier w Dublinie. Zagadka składała się z drewnianego, regularnego dwunastościanu o dwudziestu rogach, gdzie każda ściania miała kształt regularnego pięciokąta i trzech krawędzi zbiegających się w każdym rogu (rys. 5.2).

Rogi oznaczane były nazwami dwudziestu znanych miast, m. in. takich jak : Londyn, Nowy Jork, Delhi, Paryż. Zadaniem osoby rozwiązującej łamigłówkę było znalezienie drogi wzdłuż krawędzi dwunastościanu przechodzącej przez każde z 20 miast dokładnie jeden raz. Chociaż rozwiązanie tego specyficznego zagadnienia można łatwo uzyskać manualnie, to do dzisiejszego dnia nikt nie znalazł warunku koniecznego i wystarczającego na istnienie takiej drogi (zwanej obwodem Hamiltona) w dowolnym grafie. Nie jest oczywistym, ale po kilku próbach można się upewnić, że grafy pokazane na poniżej przedstawionym rys. 5.3 nie mają obwodu Hamiltona.

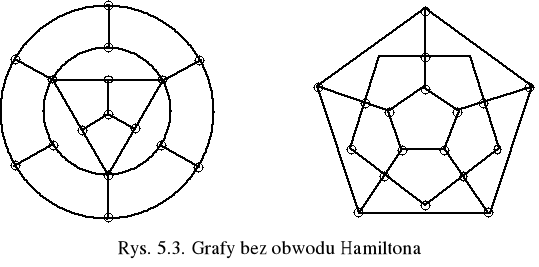
Jeśli usuniemy dowolny łuk z obwodu Hamiltona, to otrzymamy ścieżkę, zwaną ścieżką Hamiltona. Każdy obwód Hamiltona ma ściezkę. Istnieje wiele grafów ze ścieżkami Hamiltona, które nie mają obwodu Hamiltona.

Można wykazać, że całkowita liczba różnych obwodów w digrafie pełnym o n wierzchołkach wynosi (n-1)! (w grafie niezorientowanym ta liczba jest o dwa razy większa).

Silnie związanym z zagadnieniem obwodów Hamiltona jest problem komiwojażera, określony w następujący sposób: komiwojażer w czasie swojej podróży musi odwiedzić pewną liczbę miast. Odległości między miastami są znane. W jakiej kolejności powinien on odwiedzać każde z miast, tak aby w każdym z nich znaleźć się dokładnie jeden raz i wrócić do domu przebywając najmniejszą liczbę kilometrów? Do tego typu zagadnień odnosi się nasze zadanie projektowe. Zamiast miast odwiedzamy sklepy z pieczywem, a rolę domu spełnia piekarnia. Teoretycznie problem komiwojażera można zawsze rozwiązać poprzez wyliczenie wszystkich (n-1)! obwodów Hamiltona, obliczenie kosztów lub czasu przejazdu w każdym obwodzie, a następnie wybranie najtańszej (najkrótszej) z nich. Zaś dla dużej wartości n wymagany wkład pracy jest zbyt duży, nawet przy użyciu nowoczesnego komputera. Warto np. oszacować czas szukania najkrótszego obwodu Hamiltona dla 50 stolic Stanów Zjednoczonych. Zauważmy, że problem komiwojażera znajduje zastosowanie w badaniach operacyjnych.

Istnieje jeszcze szereg dostępnych heurystycznych metod rozwiązywania tego problemu, które dają drogę Hamiltona bardzo zbliżoną do najkrótszej, ale nie gwarantują jej najmniejszej długości.

Algorytmy szukania obwodów Hamiltona

Łatwo udowodnić, że algorytmy szukania obwodów Hamiltona są ciasno powiązane z permutacjami oraz didrzewami. Z jednej strony permutacje na zbiorze numerów oznaczają, że każdy wierzchołek digrafu będzie odwiedzony dokładnie jeden raz, co jest niezbędnym warunkiem istnienia obwodu Hamiltona. Niestety warunek permutacji nie jest wystarczający, ponieważ można odwiedzać jakąś grupę wierzchołków w lokalnych cyklach. Dla wystarczającej decyzji dotyczącej istnienia obwodu Hamiltona należy sprawdzić czy są ścieżki od każdego wierzchołka do korzenia.

Dualny algorytm szukania obwodu Hamiltona oparty jest na sprawdzeniu numerów wierzchołków każdego didrzewa, oraz możliwości ich należenia do permutacji. Innymi słowy, drzewem Hamiltona nazwiemy takie drzewo grafu G, w którym indeksy w tablicy drzewa DV są różne (drzewa typu łańcuch). Dla przejścia od drzewa Hamiltona do drogi (ścieżki, obwodu, szlaku) Hamiltona wystarczy dodać do niego łuk wychodzący z wierzchołka którego numer nie jest obecny w tablicy DV. Łatwo zauważyć, że dodatkowy łuk zawsze wychodzi od korzenia. Dla komputerowej generacji ścieżek Hamiltona należy generować kombinacje IK z n-1 zbiorów łuków. Każdy taki i-ty zbiór (i=1...n-1) mieści łuki wychodzące z i-tego wierzchołka. Po sprawdzeniu drzewa należy wyznaczyć, czy w wektorze DV nie ma powtarzających się indeksów. Kiedy „TAK” - to dane drzewo jest drzewem Hamiltona.

Dla generacji obwodu Hamiltona należy wyznaczyć, jaki z indeksów 1...n-1 nie jest obecny w wektorze DV. Obliczony indeks zanotujemy na pozycji zerowej wektora DV. W takiej postaci wektor DV informuje o obwodzie Hamiltona. Dla obliczenia wagi (wartości) obwodu Hamiltona należy dodać wartości łuków owej drogi.

---