60621

Materiały dydaktyczne - Geodezja geometryczna Marcin Ligas. Katedra Geomatyki. Wydział Geodezji Górniczej i Inżynierii Środowiska

Rozwiązywanie tego problemu bezpośrednio na elipsoidzie niepotrzebnie komplikuje rachunki zwłaszcza, iż na podstawie związków między współrzędnymi kartezjańskimi a geodezyjnymi natychmiastowo otrzymujemy długość geodezyjną A.

y

A = aretan—

Jednakże, równanie to posiada wadę, dzielenie pizez “0” wówczas, gdy Xg = 0. Wadę tę można ograniczyć, VermeiUe podaje następującą zależność:

A = — - 2 aretan . ^X°-, dla y_a £ 0

² Jxl+yo⁺y₀

oraz

A = -—+ 2 aretan^Yg -, dla y_Q < 0

² 4*o⁺yl ~y₀

W celu znalezienia szerokości oraz wysokości geodezyjnej łatwiej przejść na elipsoidę południkową (w przypadku elipsoidy obrotowej każdy przekr ój południkowy jest taką samą elipsą). Choć i takie uproszczenie zagadnienia wcale nie czyni go trywialnym (może ktoś z Was spróbuje go rozwiązać).

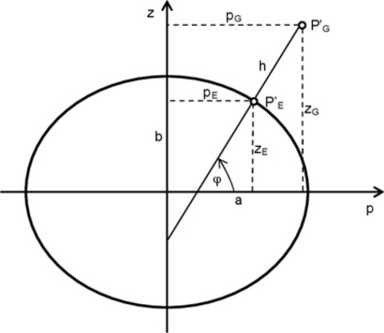
Rysunek 2: Współrzędne (<p, h), elipsa południkowa

Problem przeliczania współrzędnych jest bardzo popularny w literaturze geodezyjnej, można powiedzieć, że co roku pojawia się jakieś nowe rozwiązanie problemu. Rozwiązania tego zadania można podzielić na ścisłe oraz iteracyjne. Ścisłe rozwiązania polegają na rozwiązaniu równania czwartego stopnia ze względu na różne (w zależności od metody) parametry. Iteracyjne natomiast polegają na szukaniu kolejnych przybliżeń parametru, który rozwiązuje zadanie. W tym konspekcie przedstawiono dwie metody iteracyjne: metodę Bowringa (w ujęciu Fukushimy) oraz metodę Fukushimy.