60622

Materiały dydaktyczne - Geodezja geometryczna Marcin Ligas. Katedra Geoinatyki. Wydział Geodezji Górniczej i Inżynierii Środowiska

d²z 1 dq> _    1__1_

dp²    sin²ę><$> sin² (p dp

d(p

dp _ -a(l-g²)siny

^    (l-<?²sin²ę>)2

d²z _ -(l-e² sin² (p)-dp² <j(l-e²)sin³</>

otrzymujemy formułę na promień krzywizny południkowej M:

M = 4-^gi) ,

<P\²

PROMIEŃ KRZYWIZNY W PIERWSZA WERTYKALE

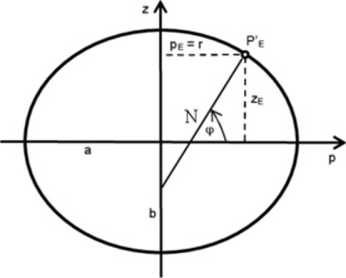
Płaszczyła równoleżnika piuiktu P tworzy z płaszczyzną pierwszego wertykalu kąt (p, zatem promień równoleżnika można wyrazić za pomocą promienia krzywizny w pierwszym wertykale:

r = p_E= N cos (p

ocosq>

yjl-e²sm² (p

stąd promień krzywizny w pienvszym wertykale jest równy:

a

N

>/T

e² siu² (p

Pierwsza forma kwadratowa powierzchni

Mając daną powierzchnię zadaną równaniami parametrycznymi:

x = x(ę_yX) y=y(<p,A)

(1)