82422

Część 2 6. KOMPUTEROWA WERSJA METODY PRZEMIESZCZEŃ 15

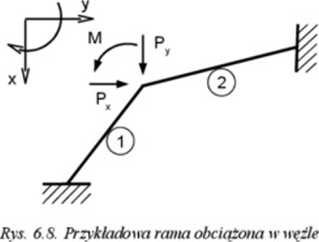
Ponieważ luniemy znaleźć i przetransformować włości reakcji pizywęzłowych od obciążeń przęsłowych występujące na pojedynczych piętach ramy, narysujmy je dla każdego pręta (rys. 6.9) w odniesieniu do globalnego układu współrzędnych (po transformacji).

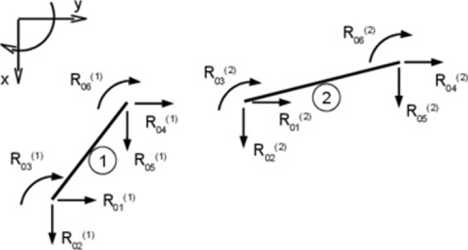
Rys. 6.9. Reakcje przywęztowe w globalnym układne współrzędnych

Pamiętając, że globalne kierunki reakcji pokrywają się z globalnymi kierunkami pizemieszczeń (rys. 6.1), możemy stwierdzić, że na przykład kierunek reakcji Roł^h pokiywa się z kierunkiem pierwszego przemieszczenia qi. a kienmek reakcji Roś¹' pokrywa się z kierunkiem piątego przemieszczenia q.<. Podobne zależności można zapisać dla pręta drugiego, np.: kienmek reakcji Rot'^2, pokrywa się z kierunkiem czwartego przemieszczenia q* Możemy zatem zestawić te wiadomości w tabeli alokacji (tabela 6.5). w pierwszym wierszu cyfiy od 1 do 6 oznaczają sześć kolejnych kieiunków w dowolnym elemencie, zgodnych z układem globalnym (wskaźnik i w symbolu Rei^h ). W kolejnych wierszach podano jakim kienmkom globalnych przemieszczeń (rys. 6.1) odpowiadają one w poszczególnych elementach.

Tabela 6.5. Tabela powiązali dla elementów wektora obciążeń

	niuner reakcji R*
nr pręta	1	2		3	4	5	6
1	1	2		3	4	5	6
i	4	5		6	7	8	9

AlmaMater

Dobra D.. Dztakicwlcz L.. Jatnbrożrk S.. Ko«n<na M.. Mikołajczak E„ Przvfoyl«ka P., Syrak A , Wdowdca A.