82477

Część 2 6. KOMPUTEROWA WERSJA METODY PRZEMIESZCZEŃ 19

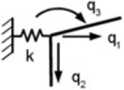
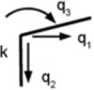
Obecność podpory sprężystej w węźle ramy uwzględniamy nieco inaczej niż obecność sztywnych podpór. Ma ona bowiem wpływ na macieiz sztywności, a nie jak było do tej pory. na wektor niewiadomych przemieszczeń. Modyfikacji dokonujemy przez dodanie parametru sztywności k podpory sprężystej do odpowiadającego numerowi jej kierunku wyrazu z przekątnej macierzy sztywności układu

R*=q,-

Rys. 6. JO. Podpora sprężysta u uężle ramy

W przypadku podpory sprężystej z rys. 6.10, sztywność k dodamy do wyrazu Kn w macierzy sztywności układu, ponieważ kierunek reakcji Rt w sprężynie pokrywa się z kierunkiem pierwszego przemieszczenia.

Zastanówmy się zatem, które przemieszczenia będą zerowe w przykładzie z rys. 6.1. Rama ma utwierdzenia w dwóch węzłacli, możemy zatem napisać, że przemieszczenia w tycli węzłach są równe zero:

⁽1, =<J₂=<Jj=<J=<Ji=<J₉=0

Wynika z tego. że niezerowe są tylko trzy pozostałe przemieszczenia:

<1**0 <Is *0 <1**0

Wyzerujmy teraz w wektorze obciążeń wiersze, a w macierzy sztywności wiersze i kolumny, odpowiadające zerowym przemieszczeniom. Na przykład przemieszczenie po kierunku pierwszym jest zerowe, możemy więc "wyzerować" pierwszy wiersz w wektorze obciążeń, oraz pierwszy wiersz i pierwszą koliuruię w macierzy sztywności układu Jeżeli nie zmieniamy wymiaru macierzy ("zerowe" wiersze pozostają) to na głównej przekątnej należy wpisać jedynki. W ten sposób mnożenie pierwszego wiersza macierzy sztywności przez wektor przermeszczeń daje wmunek q_t = 0. Jeśli tego nie uczynimy macierz sztywności będzie osobliwa (nie ma r ozwiązań).

I	0	0	0	0	0	0	0	0		<1 /		0
0	1	0	0	0	0	0	0	0		<1:		0
0	0	1	0	0	0	0	0	0		<Ii		0
0	0	0		Ku	K„	0	0	0		<1,		R*
0	0	0	K»	Ku	Ka	0	0	0		<Ii	=	R*
0	0	0	K„	Ka	km	0	0	0		<16		Re
0	0	0	0	0	0	I	0	0		<!•		0
0	0	0	0	0	0	0	1	0		<ls		0
0	0	0	0	0	0	0	0	1		<1*		0

Jeżeli do rozwiązania układu równań użyjemy programu komputerowego, nie będzie miało znaczenia, jakiego jest on wymiaru. Do obliczeń ręcznych w^fskazane byłoby wykreślenie "wyzerowanych" wierszy i kolumn Wtedy pozostaną tylko trzy równania:

AlmaMater

Dobra D.. Dztakicwlcz L.. Jatnbrożrk S.. Ko«n<na M.. Mikołajczak E„ Przybyl«ka P., Syrak A.. Wdowdca A.