82479

Część 2 6. KOMPUTEROWA WERSJA METODY PRZEMIESZCZEŃ 12

Ł\
l		/ **
0		0
0		0
-K-i		^KiAx
1
0		0
0		0 » 1

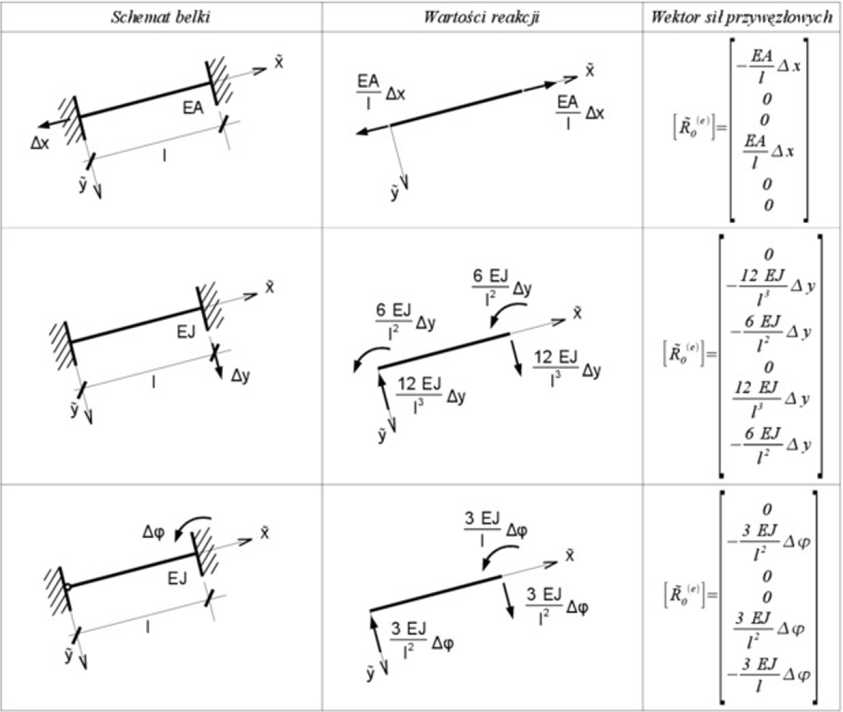
W tabeli 6.4 podano kilka przykładów wyznaczania wektora sił przywęzłowych od przemieszczeń (osiadali) węzłów.

Tabela 6 i Wartości reakcji k '₀ od osiadali podpór

Do tej pory zapisywaliśmy macierze sztywności i wektory sil pizywęzlowych dla pojedynczych prętów, w ich lokalnych układach współrzędnych. Jednak w celu rozwiązania zadania (ramy wieloprętowęj) korzystamy z równania równowagi zapisanego dla całego układu (6.1). Zawiera ono macieiz sztywności, wektor przemieszczeń oraz wektor obciążeń stwoizony dla wszystkich prętów. Do utworzenia potizebnych

AlmaMater

Dobra D.. Dztakicwlcz L.. Jatnbrożrk S.. Ko«n<na M.. Mikołajczak E„ Przvfoyl«ka P., Syrak A., Wdowdca A.