82427

Część 2 6. KOMPUTEROWA WERSJA METODY PRZEMIESZCZEŃ 5

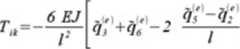
Podstawiając związki (6.7) otrzymamy poprawny wzór transformacyjny:

+<Pt~2 «/',*]

Na koniec rozpiszmy jeszcze pierwszy wiersz równania (6.3). pamiętając, że kj =-N_lk:

(6.9)

Ponieważ przeinieszczeiua q^f, i q, to przemieszczenia końców pięta wzdłuż jego osi. ich różnicę możemy nazwać wydłużeniem lub skróceniem pręta:

Ostatecznie otrzymujemy wartość siły normalnej N,t. która spełnia związki fizyczne:

W ten sam sposób można rozpisać każdy z wierszy równania (6.3). otrzymując tym samym odpowiedni wzór transformacyjny metody przemieszczeń.

Nie zawsze jednak mamy do czynienia wyłącznie z piętami obustronnie utwierdzonymi. Jeżeli w skład ramy wchodzą także pręty zakończone pizegubem, mamy dwie możliwości postępowania. Jedna z nich polega na rozwiązywaniu układu z założeniem, że wszystkie pręty są obustronnie utwierdzone, a przegub uwzględniany jest dopiero przy modyfikacji układu ze względu na warunki podparcia Druga metoda pozwala na uwzględnienie przegubu już na początku obliczeń pizez wykonanie tak zwanej redukcji statycznej.

6.3. Redukcja statyczna

W pizypadku prętów z przegubem znamy wtuIość jednej z reakcji R,'^f . W miejscu przegubu wartość momentu Mt lub A/*, (w zależności czy przegub jest na lewym czy prawym końcu pręta) wynosi zero (rys. 6.3).

Rys. 6.3. Pręty z przegubem: na lewym i pranym kołku

AlmaMater

Dobra D.. Dztakicwlcz L.. Jatnbrożrk S.. Ko«n<na M.. Mikołajczak E„ Przybyl«ka P., Syrak A., Wdowdca A.