82426

Część 2 6. KOMPUTEROWA WERSJA METODY PRZEMIESZCZEŃ 2

^rl,	^r'2	^rn	^r,4 •	• ',9
^r2/	^Tii	^r:t	^r24 •	r 29
r,t	r*:		r„ .	• ^r>9
^r9l	r92	^r9S	^r9t	^r 99

Niewiadome, oznaczane dotąd Z to nic innego jak szukane przemieszczenia węzłów <7,. które tworzą macierz niewiadomych przemieszczeń węzłowych [</]:

<1,

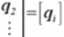
<79

Współczynniki» również będą tworzyły macierz - tak zwany wektor obciążeń [/*„]:

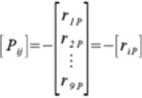
Można zatem cały układ równali kanonicznych zapisać w postaci równania macieizowęgo: lub ogólniej dla dowohiego układu (w to liczba niezależnych przemieszczeń węzłowych)

I^U*kLx/=(^U    (6-1)

Rozwiązanie równania (6.1) pozwoli nam uzyskać wynik, tak jak w zadaniu klasycznym. Aby jednak móc przystąpić do obliczeń, należy utworzyć wszystkie podzebne macierze. Każda z nich powstaje w wyniku agregacji odpowiednich macierzy elementowych (zapisanych dla pojedynczych prętów).

Przyjrzyjmy się zatem pojedynczemu elementowi ramy (<»). Przyjmujemy lokalny układ współrzędnych xy. taki. że oś x pokrywa się z osią pięta, a oś y jest do mej prostopadła i tworzą układ prawoskrętny (oś .v obraca się w kierunku osi y zgodnie z ruchem wskazówek zegaia). W takim układzie lokalnym numerujemy przemieszczema oraz reakcje. Dla pręta obustronnie utwierdzonego trzeba określić sześć reakcji w węzłach (każdemu przemieszczeniu musi odpowiadać reakcja po tym samym kierunku)

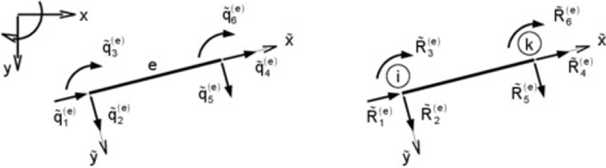
Rys. 6.2. Lokalne kie notki przemieszczeń i reakcji

AlmaMater

Dobra D.. Dztakicwlcz L., Jatnbrożrk S.. Ko«n<na M„ Mikołajczak Z.. Przybylfka P., Syrak A , Wdowdca A.