82475

Część 2 6. KOMPUTEROWA WERSJA METODY PRZEMIESZCZEŃ 14

Transformacja pozwala nam uzyskać składowe macierzy sztywności i wektora sil przywęzłowych. odniesione do globalnego układu współrzędnych. Składowe wektora sił będą wyrażały teraz reakcje zorientowane zgodnie z osiami globalnego układu współrzędnych (rys. 6 .7).

Część 2 6. KOMPUTEROWA WERSJA METODY PRZEMIESZCZEŃ 14

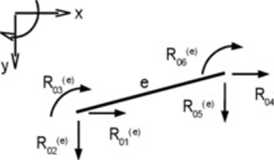
Rys. d 7. Kierunki reakcji od obciążeńprzęsłowych ir globalnym układzie współrzędnych (po transformacji/

Jak widać na rys. 6.7, reakcje R'_0f i R¹^ nie zmieniły kierunku. Ponieważ momenty przy węzłowe nie zależą od pizyjętego układu współrzędnych, nie zmieniła się także icli wartość:

R<*. ⁼&(r,

Dysponując macierzami zapisanymi w jednolitym układzie współrzędnych możemy dokonać iclr agregacji (złożenia).

6.6. Agregacja macierzy

Agregacja macierzy polega na odpowiednim ułożeniu poszczególnych składników' macierzy zapisanych dla kolejnych elementów w odpowiadające im pola w macierzy całkowitej (dla całej konstrukcji). Agregować można składowe wielu macieizy elementowych pod w^raiiuikiem. że wszystkie dotyczą jednego, globalnego układu współrzędnych.

Aby ułatwić sobie odnajdywanie miejsc właściwego położenia poszczególnych elementów', skorzystamy z tak zw^fanej tabeli alokacji (powiązań). Nie ma uniwersalnej tabeli alokacji. Trzeba sporządzić ją dla każdego zadania oddzielnie, ale korzystamy z niej zarówno do agregacji macierzy sztywności, jak i wektora obciążeń. Tworzeniu takiej tabeli przyjrzymy się agregując wektor obciążeń.

6.6.1. Agregacja wektora obciążeń

Analizie poddamy ramę obciążoną silanu węzłowymi, w której obciążenie przęsłow^re może być dowolne (zakładamy zerowa). Istotne jest. aby siły przyłożone w węźle pokrywały się z globalnym układem współrzędny cli. Gdyby jednak działały w dowolnym kierunku, trzeba by je rzutować i w każdym w-ężle wyr azić jako składowa równoległe do osi globalnego układu współrzędnych.

AlmaMater

Dobra D.. Dztakicwlcz L.. Jatnbrożrk S.. Ko«n<na M.. Mikołajczak E„ Przybyl«ka P., Syrak A., Wdowdca A.