6827069121

EGZAMIN Z ANALIZY MATEMATYCZNEJ I

Data: ............................

Wynik egzaminu:.........../ pkt

Ocena:

Studia: dzienne/zaoczne*

Imię i nazwisko, nr indeksu: .....

Nazwisko prowadzącego ćwiczenia

Ocena z ćwiczeń: ................

*- niepotrzebne skreślić

1.    Niech a_n = dla n € N. Wówczas ciąg (a„):

(a)    jest/nie jest ograniczony, bo .........................................................................................

(b)    posiada/nie posiada podciągu zbieżnego do 0, bo ...................................................................

/pkt]

2.    Jeśli lim a_n = 2 oraz lim b_n = oo, przy czym a_n, b_n > 0 dla n € N, to

(a)    Jlim^=............................................ (c)    + ^-)^a" -......................................

(b)    lim \/b^ —............................................ (d) lim (a_n)^fc" =..........................................

(w przypadku braku jednoznacznej odpowiedzi piszemy tylko odpowiedni symbol)    |    /pkt |

3. Niech a_n = (—2)" dla n € N. Wówczas szereg Y1 °n ’■

(a)    jest zbieżny/rozbieżny, bo..........................................................................................

(b)    spełnia/nie spełnia warunku koniecznego zbieżności szeregów liczbowych, bo........................................

..........................................................................................................|    /pkt |

4. Kryterium Leibniza:

Szereg ^ (—l)ⁿ(l — L)ⁿ jest zbieżny/rozbieżny na mocy kryteriui

...............................................................................................................|    /pkt |

5. Definicja asymptoty pionowej:..........................................................................................

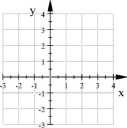
Naszkicuj wykres funkcji / : R —► R, jeśli wiadomo, lim f(x) = 0, lim₊ f(x) = +oo, lim (f(x) + x) = 0, lim f(x) = 0.

Jakie asymptoty na pewno posiada taka funkcja?