5555241351

Obliczmy teraz przykładowo jedną pochodną cząstkową z powyższego wyrażenia :

da

1

Hy_L-yc))

y_L-yc

Ay_L

<*L    _{[ t} (y_L -yę)¹    (^L-^c)² (x_L -X_c)² + (y_L -y_c)^! Ax²L+AyJ

(x_L — x_c)

W podobny sposób oblicza się pozostałe pochodne cząstkowe :

Ay, _D    Ax_r

= B_l (7)

da	Axl		da
<^L	Ax^2l + Ay^2L		dx.p
da	AyL	i ^Ay	p
ćkc	Ax^ + Ay^	Axp +	Ay l
da	Axl	Ax	p
	AXl + Ay^z	Axp +	AyJ

r = -B_p

r = A_p

(8)

(9)

_t = -(A_l-A_p)

(10)

Ostateczna postać równania poprawki kata będzie następująca:

\_a = B_l dx_L - A_l dy_L -B_p dx_p +A_P dy_p -(B_L -B_p) dx_c +(A_L - A_p) dy_c+I (11) 3.2.Równanie poprawki boku (odległości).

Dla boku przedstawionego na rys.4 można z kolei przedstawić następującą zależność :

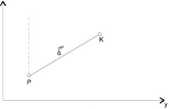
rys .4

d^obs + Vd = dd + d^prz, a po uporządkowaniu Vd = dd + d^prz - d^obs = dd + I    (12)

a I = d^prz - d^obs to podobnie jak przy kątach - wyraz wolny

Bok pomierzony (zaobserwowany) d^obs plus nieznana poprawka Vd ma się równać różniczce zupełnej dd funkcji boku d plus przybliżony bok d^prz . Wzór na różniczkę zupełną boku będzie następujący:

eto

dy_P

dy_P

eto

(k_K

(13)

Bok d można przedstawić posiłkując się współrzędnymi następująco :

(14)

d=V(^xK —Xp)² + (y_K — y_P)²