6628927038

Tadeusz W.Boh, Wykłady z ekonometrii

Model rynku w równowadze nazywamy modelem o równaniach współzależnych, gdyż wyróżnia się występowaniem jednoczesnych powiązań zwrotnych między zmiennymi łącznie współzależnymi. Pow iązania zwrotne mogą mieć charakter bezpośredni, tak jak w przy padku modelu (1.13) lub pośredni.¹

Aby poznać istotę modelu rekurencyjnego przypomnijmy znany model rynku w równowadze, nazywany modelem pajęczyny. Ma on postać:

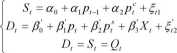
(1.14)

Oznaczenia zmiennych są analogiczne jak w pierwszym staty cznym modelu rynku. Różnica między' tymi modelami polega „tylko" na opóźnionej reakcji podaży na zmianę ceny. Obecnie omawiamy zatem dynamiczny model ry nku.

Podobnie jak poprzednio przekształćmy model tak, by zawierał tylko dwa równania. W konsekwencji przekształceń otrzymamy:

l

Q, -a₀ +a_lp,__l +a₂p^c, +£„

__Pt =p₀+m+frp;+frx,+{n

(1.15)

gdzie: P_Q=P'JP[, p, =-HP[, P₂ = P'JP[, P_y =P\!P[, £₂ =£,/#•

Zbiór zmiennych łącznie współzależnych tego modelu zaw iera nadal zmienne: Q, i p,, natomiast do zbioru zmiennych z góry ustalonych zaliczamy:    , p\, p‘, X, . W modelu pajęczyny jednak wielkość

zrealizowanego popytu wpływa na cenę, natomiast bezpośrednia zależność zw rotna nie występuje. Cena nie wpływa na w ielkość zrealizowaną bezpośrednio, lecz z jednookresowym opóźnieniem. Zależność tego typu przedstaw ia graf zamieszczony poniżej.

Model, w którym zależności między zmiennymi występują w postaci jednokierunkowego (niezw rotnego) łańcucha powiązań, nazywamy modelem rekurencyjnym. Model pajęczyny należy do klasy modeli rekurencyjnych.

Ostatnim z rozpatry wanych rodzajów modeli wielorównaniowych są modele proste. Model prosty to taki, w którym nie występują bezpośrednie powiązania między zmiennymi łącznie współzależnymi. W takim modelu, w zbiorze zmiennych objaśniających występują tylko zmienne z góry' ustalone.

Najczęstszym przykładem modeli prosty ch są układy mikrorelacji, opisujące zachowanie pewnego zbioru jednostek ekonomicznych (np. przedsiębiorstw, gospodarstw domowych, grup towarów itp.). Np. Y.Grunfeld i Z.Griliches² rozpatrywali model inwestycji przedsiębiorstw, w którym inwestycje j-tej spółki

15

1

   Przykład takiego modelu zmieszczony jest w następnym punkcie części tego wykładu.

2

   Zob. Y. Grunfcld, Z. Griliches, Is Aggregation Neccssarily Bad, Review of Economics and Statistics. 1960, vol. 42, str. 1-13.