130859381

10

E. Koźniewski: Geometria odwzorowań inżynierskich, powierzchnie 05A

Rys. 5A-13: Ilustracja konstrukcji siatkowej elipsy: a) danej za pomocą, średnic sprzężonych ćwiczeniem w rysowaniu za pomocą edytora graficznego (AutoCAD).

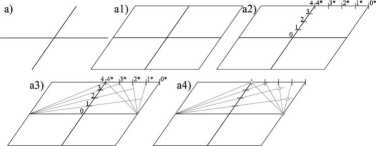
Rozwiązanie zadania 2B. Opis rozwiązania przeprowadzimy komentując sekwencję rysunków 5A-15 -r 5A-17. Zakładamy (rys. 15a), że:

rys. 5A-15a) dana jest elipsa o danych dwóch średnicach sprzężonych przy czym średnice te muszą być zadane zgodnie z zasadami aksonometrii prawieprostokątnej (3:4), to znaczy przyjmujemy układ osi aksonometrii i dwa połowiące się odcinki jeden wzdłuż osi Oy, drugi skrócony w stosunku 3:4 wzdłuż osi Ox (na rys. 15a średnice sprzężone przyjęto w dowolnej aksonometrii);

rys. 5A-15al) w celu odwzorowania elipsy na okrąg konstrujemey oś powinowactwa równoległą do jednej ze średnic przechodzącą przez koniec drugiej (to ostatnie założenie nie jest konieczne ale wygodne);

rys. 5A-15a2) konstruujemy równołegłobok i odpowiadający mu kwadrat definiujący powinowactwo; rys. 5A-15a3) rysujemy okrąg i

rys. 5A-15a4) dzielimy go na n (n=16) równych części;

rys. 5A-16a5) przekształcamy przez powinowactwo otrzymane punkty rysując przez dwa z tych punktów prostą w układzie okręgu; rys. 5A-16a6) znajdujemy obraz tej prostej;

rys. 5A-16a7) znajdujemy obrazy dwóch punktów leżących na tej prostej;

rys. 5A-17a8) przekształcamy przez powinowactwo otrzymane pozostałe punkty równomiernego

podziału okręgu, otrzymujemy punkty podziału elipsy (n = 16 punktów);

i

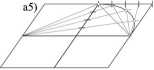
rys. 5A-17a9) rysujemy drugą, przesuniętą równolegle, elipsę i łączymy punkty dolnej elipsy z punktami górnej elipsy przyjmując przesunięcie o t(t = 4) punktów. Należy dodać, że ustawienie prostej tworzącej względem osi obrotu jest zupełnie dowolne.

Na rysunku 5A-17a9 narysowano tylko jedną rodzinę prostych, by rysunek ten był możliwie jak najbardziej czytelny. Otrzymana powierzchnia może pełnić w praktyce interersujące funkcje