130859383

12

E. Koźniewski: Geometria odwzorowań inżynierskich, powierzchnie 05A

Rozmazanie zadania 2C. Za pomocą polecenia REVSURF/POWOBROT tworzymy hiper-boloidę obrotową. Przyjmujemy prostą pionową oraz inną prostą skośną (PLINE/PLINIA z użyciem filtru na przykład .xy).

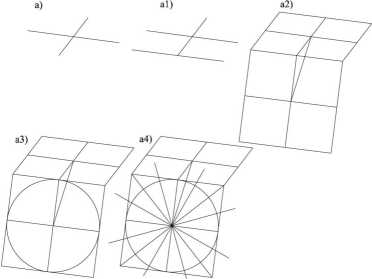
Rys. 5A-15: Wykorzystanie powinowactwa i pośrednictwa okręgu do konstrukcji elipsy wraz z punktami równomiernego podziału: a) elipsa dana za pomocą średnic sprzężonych; al) wybór osi powinowactwa; a2)-a4) konstrukcja okręgu - obrazu elipsy wraz z punktami podziału okręgu

Zadanie 3 W oparciu o dokonany w zadaniu 1 podział stożkowej narysować (tradycyjnie p-o) w rzutach prostokątnych i w aksonometrii prawieprostokątnej (3:4) schody kręcone o ośmiu stopniach na jeden pełny obrót (rys. 5A-18).

Rozwiązanie zadania 3. Konstrukcja schodów polega na "podnoszeniu” na odpowiednią wysokość części elipsy (rys. 5A-18al -ł- rys. 5A-18a2). Jest jednak pewien szczegół mianowicie wyznaczenie stycznych pionowych do elipsy (i odpowiednich punktów styczności). Do tego celu wykorzystamy powinowactwo osiowe (rys. 5A-18a3). Oś schodów przekształcamy do układu okręgu (rys. 5A-18a3-r5A-18a4) i rysujemy proste styczne do okręgu, równoległe do przekształconej prostej (rys. 5A-19a7 4- rys. 5A-19a8), równocześnie znajdujemy punkty styczności. Następnie "wracamy” z prostymi stycznymi do układu elipsy (rys. 5A-20a9 -r rys. 5A-20al0). Znajdujemy równocześnie punkty styczności prostych pionowych do elipsy w podstawie schodów, które odpowiednio "podnosimy”. Na rys. 5A-20al0 "podniesiono” dwa punkty styczności. Rysunek 5A-21alO w powiększeniu pokazuje szczegóły konstrukcji. Przedstawiony algorytm konstrukcji schodów kręconych - to klasyczna konstrukcja za pomocą środków p-o chociaż w przestawianym materiale wykładów przedstawiona techniką komputerową 2D. Cyrklem i linijką wykonywalibyśmy te konstrukcję analogicznie. Interesującym jest również pokazać istotę konstrukcji w innej logice niż klasyczna metoda konstrukcji.