130859391

4

E. Koźniewski: Geometria odwzorowań inżynierskich, powierzchnie 05A

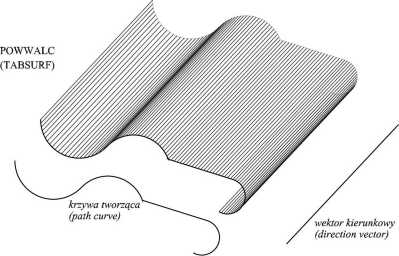
Rys. 5A-03: Powierzchnia walcowa otrzymana przez przesunięcie krzywej tworzącej (ang. path curue) wzdłuż odcinka - wektora kierunkowego (ang. direction uector)

i helikoidy:

x = (acost)u, y = (asint)u, z = —-t, t €< 0, 2tt >, u €< 0,1 > .    (9)

27r

W przypadku opisującym helikoidę powstałą przez obrót prostej w opisie parametrycznym parametr u przebiega cały zbiór liczb rzeczywistych. Przez eliminację parametrów otrzymujemy równanie powierzchni śrubowej w postaci jawnej: y — xtg=y-.

2.4. Elipsa jako obraz okręgu w powinowactwie

Spośród różnych definicji elipsy na uwagę zasługuje taka, według której elipsa jest obrazem okręgu w powinowactwie. Przyglądnijmy się tej sytuacji rozwiązując następujące zadanie.

Zadanie 1 Skonstruować elipsę jako obraz okręgu w powinowactwie określonym przez oś k i parę odpowiadających sobie punktów (0_o, O_e) (rys. 5A-07a).

Rozwiązanie zadania 1 opisane zostało na rysunkach 5A-07 -r 5A-11. Pokazano tam konstrukcję punktu elispy jako obrazu dowolnie wybranego punktu na okręgu w stosownie dobranym powinowactwie. Powinowactwo to może być zadane zupełnie dowolnie. Jednak stosowny wybór czyni całą konstrukcję bardziej elegancką i, jak się wydaje, zdecydowanie bardziej przyjazną wykonawcy. Konstrukcję taką można powtarzać dowolną liczbę razy. Wielokrotne stosowanie takiej metody byłoby jednak dość uciążliwe nawet przy załoeniu, że byłoby realizowane na komputerze. W praktyce przyjmuje się inny, o wiele prostszy, algorytm konstrukcji wynikający z własności okręgu i powinowactwa jako odwzorowania geometrycznego. Jest to tzw. konstrukcja siatkowa (rys. 5A-12). Rzecz ciekawa, że konstrukcja ta może być wykorzystana w implementacji komputerowej. Implementacja taka została zrealizowana, gdyż standardowe aplikacje programu AutoCAD zawierają funkcje rysujące elipsę