Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 1
Liczbę niezależnych współrzędnych (współ-
rzędnych uogólnionych) potrzebnych do określenia
położenia punktu lub bryły w przestrzeni nazywamy
liczbą stopni swobody
Temat: Wybrane zagadnienia kinematyki mechanizmów
Ruch punktu:
•
prostoliniowy,
•
krzywoliniowy (np. po okręgu, elipsie, dowolnej krzywej)
Ruch bryły:
•
postępowy,
•
obrotowy,
•
płaski,
•
kulisty,
•
śrubowy,
•
dowolny.
RUCH POSTĘPOWY BRYŁY
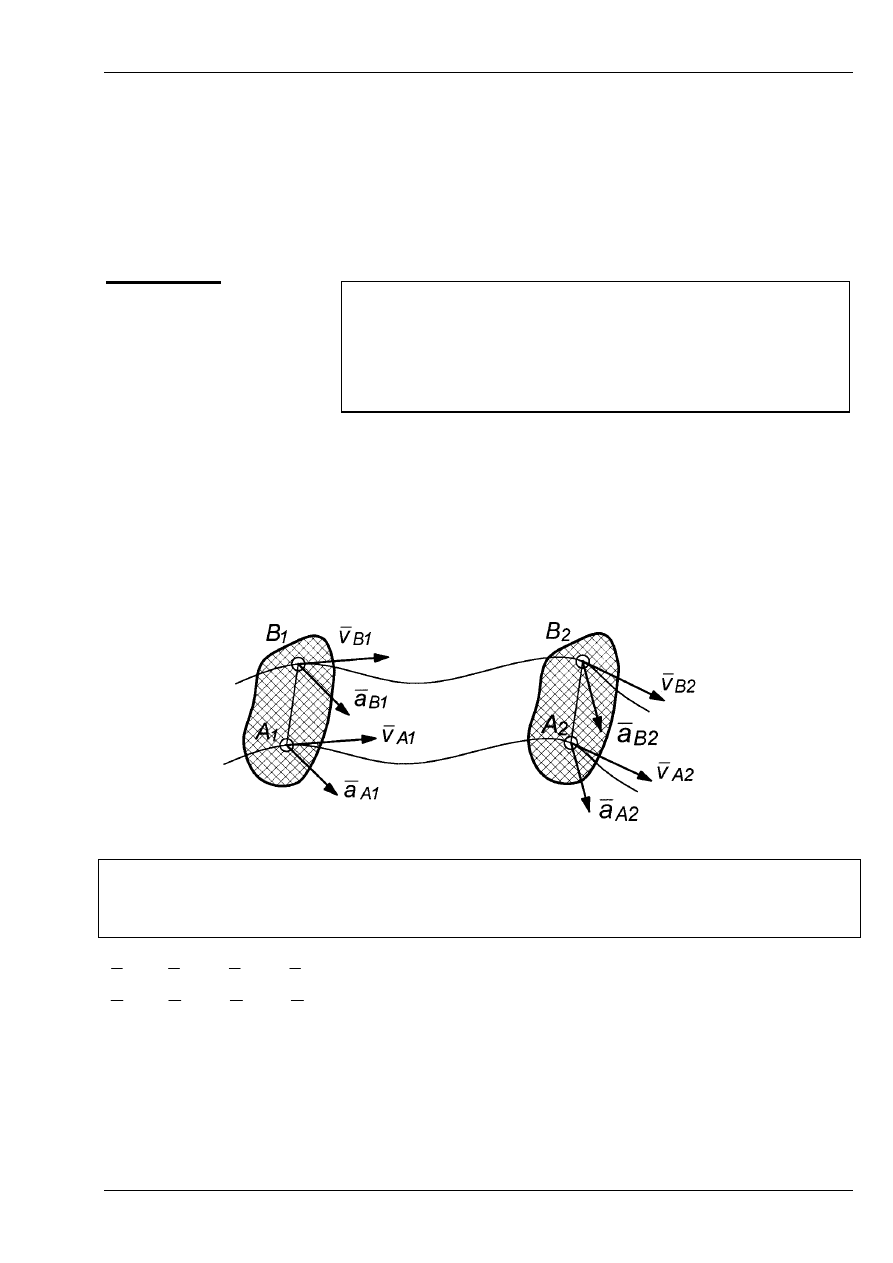
Ruch postępowy członu zachodzi wówczas, jeżeli dowolny odcinek AB zwią-
zany sztywno z członem zachowuje położenie równoległe w kolejnych położe-
niach mechanizmu: A
1
B
1
A
2
B
2
Rys. 1
Twierdzenie: Jeżeli bryła porusza się ruchem postępowym to wszystkie punkty
bryły poruszają się po torach przystających i w każdej chwili „t” mają te same
prędkości i przyspieszenia.
a
a
a
a
v
v
v
v
2
B
2
A
1
B
1
A
2
B
2
A
1
B
1
A
=
=
=
=
Równania ruchu postępowego:
)
t
(
z
z
),
t
(
y
y
),
t
(
x
x
=
=
=
x,y,z - współrzędne uogólnione
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 2
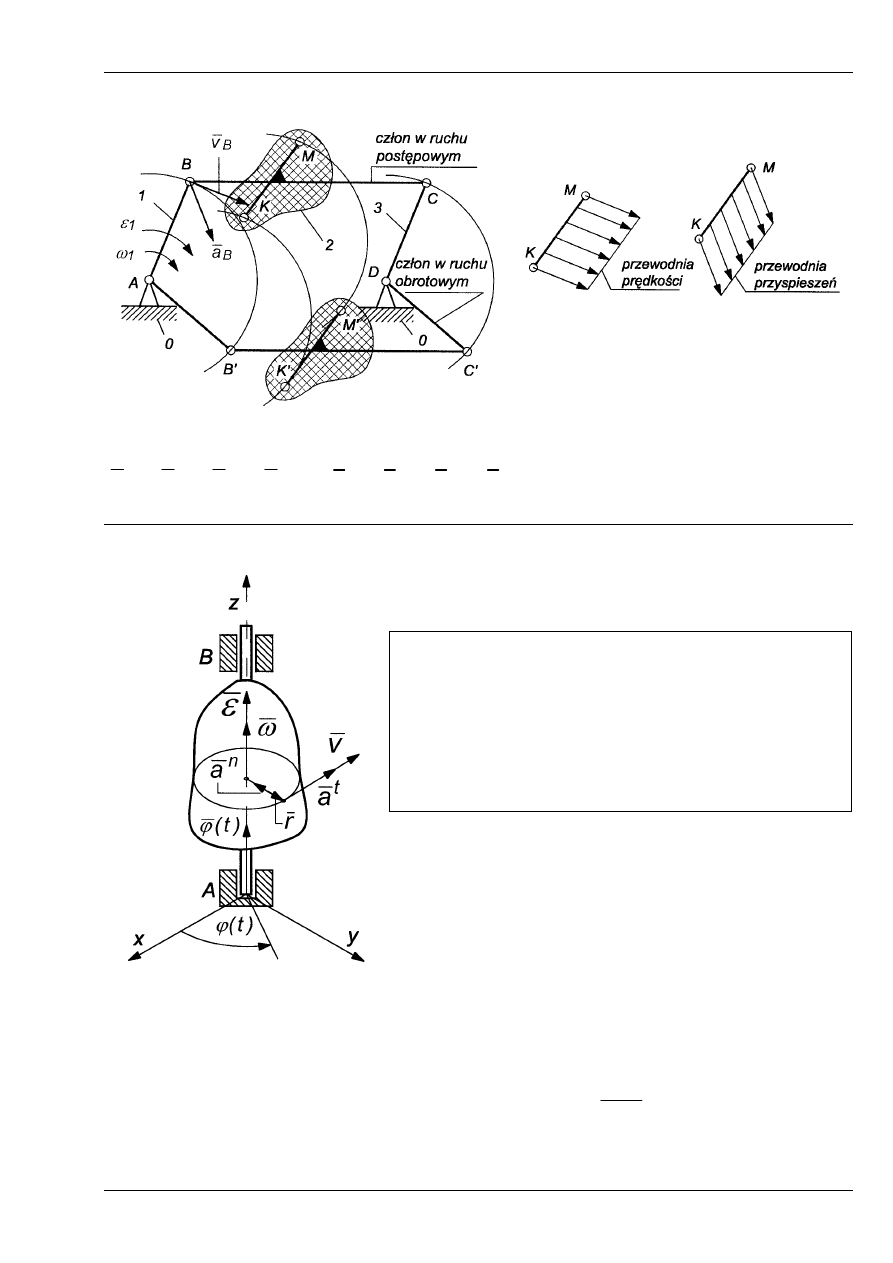
Przykład 1. Równoległobok przegubowy
Rys. 2
Tory punktów B, C, K, M są równoległe a ich prędkości i przyspieszenia równe.
M
K
C
B
a
a
a
a
=
=
=
M
K
C
B
v
v
v
v
=
=
=
0
2
=
ε
0
2
=
ω
RUCH OBROTOWY BRYŁY
Rys. 3
Bryła w ruchu obrotowym ma jeden stopień swobody,
)
t
(
ϕ
ϕ =
,
)
t
(
ϕ
- współrzędna uogólniona
Kąt obrotu bryły:
)
t
(
ϕ
ϕ =
, Prędkość kątowa:
dt
d
ϕ
ω =
Bryła wykonuje ruch obrotowy, jeżeli wszyst-
kie punkty tej bryły poruszają się po torach ko-
łowych leżących w płaszczyznach do siebie
równoległych. Środki geometryczne torów
(okręgów) leżą na jednej prostej, która jest
osią obrotu bryły.
Rozkład prędkości i przyspieszeń punk-
tów członu w ruchu postępowym.
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 3
Przyspieszenie kątowe:
dt
d
dt
d
2
2
ϕ
ω
ε
=
=
Prędkość liniowa dowolnego punktu bryły:
r
v
,
r
v
⋅
=
×
=
ω
ω
Przyspieszenie liniowe styczne dowolnego punktu bryły:
r
a
,
r
a
t
t
⋅
=
×
=
ε
ε
Przyspieszenie liniowe normalne dowolnego punktu bryły:
r
a
,
r
v
a
2
n
n
⋅
=
×
×
=
×
=
ω
ω
ω
ω
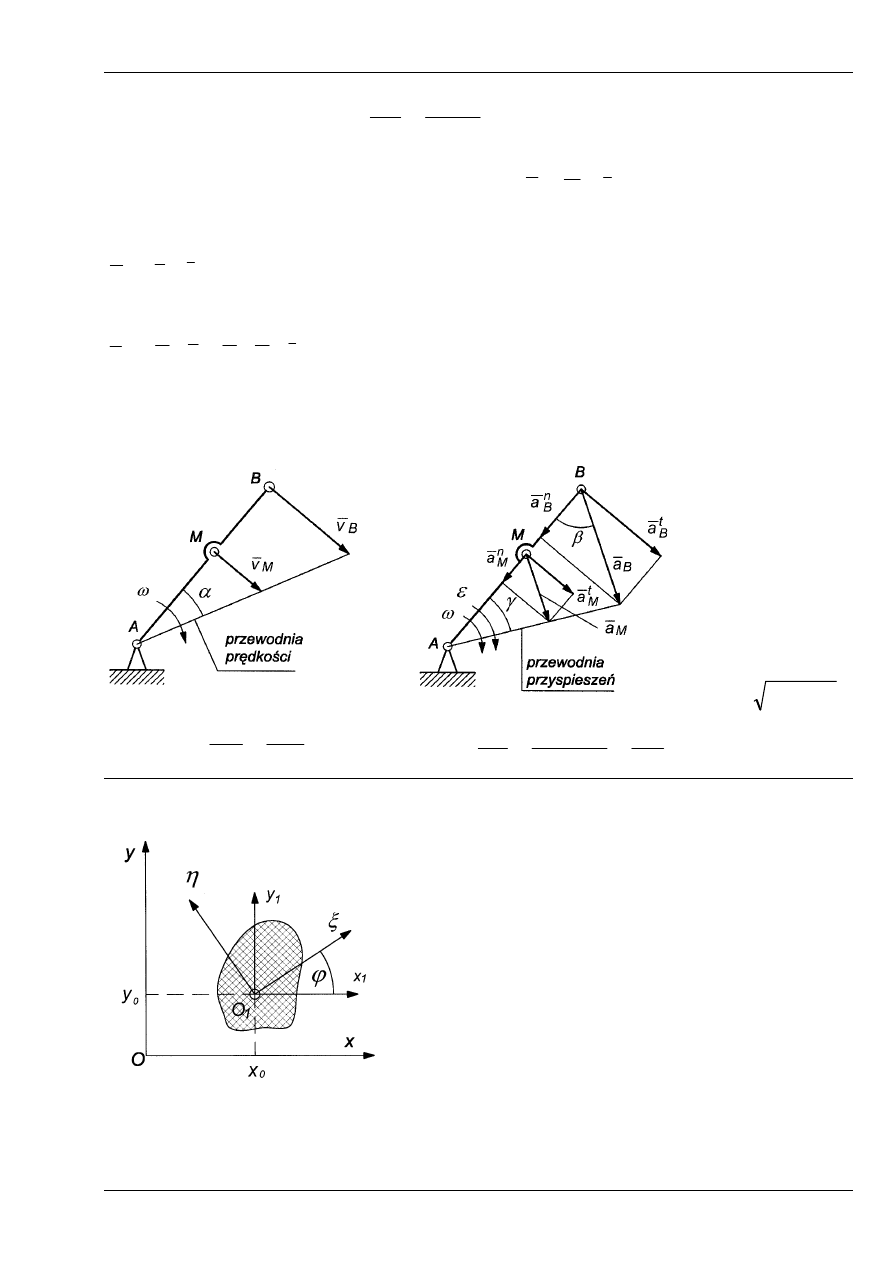
Przykład 2. Człon mechanizmu płaskiego w ruchu obrotowym
Rys. 4
RUCH PŁASKI BRYŁY
Rys. 5
Równania ruchu płaskiego:
)
t
(
),
t
(
y
y
),
t
(
x
x
0
0
0
0
ϕ
ϕ =
=
=
.
Bryła wykonuje ruch płaski, jeżeli
wszystkie punkty bryły poruszają się w
płaszczyznach równoległych do pewnej
płaszczyzny nieruchomej.
AB
a
,
AB
a
t
B
2
n
B
⋅
=
⋅
=
ε
ω
AB
v
B
⋅
=
ω
2
4
B
AB
a
ε
ω
+
=
2
2
n
B
t
B
AB
AB
a
a
tg
ω
ε
ω
ε
β
=
⋅
⋅
=
=
AM
v
AB
v
tg
M
B
=
=
=
ω
α
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 4
Twierdzenie: Jeżeli figura płaska porusza się w swej płaszczyźnie to z każde-
go położenia daje się przesunąć w inne położenie poprzez obrót dookoła punk-
tu leżącego w płaszczyźnie, zwanego chwilowym środkiem obrotu.
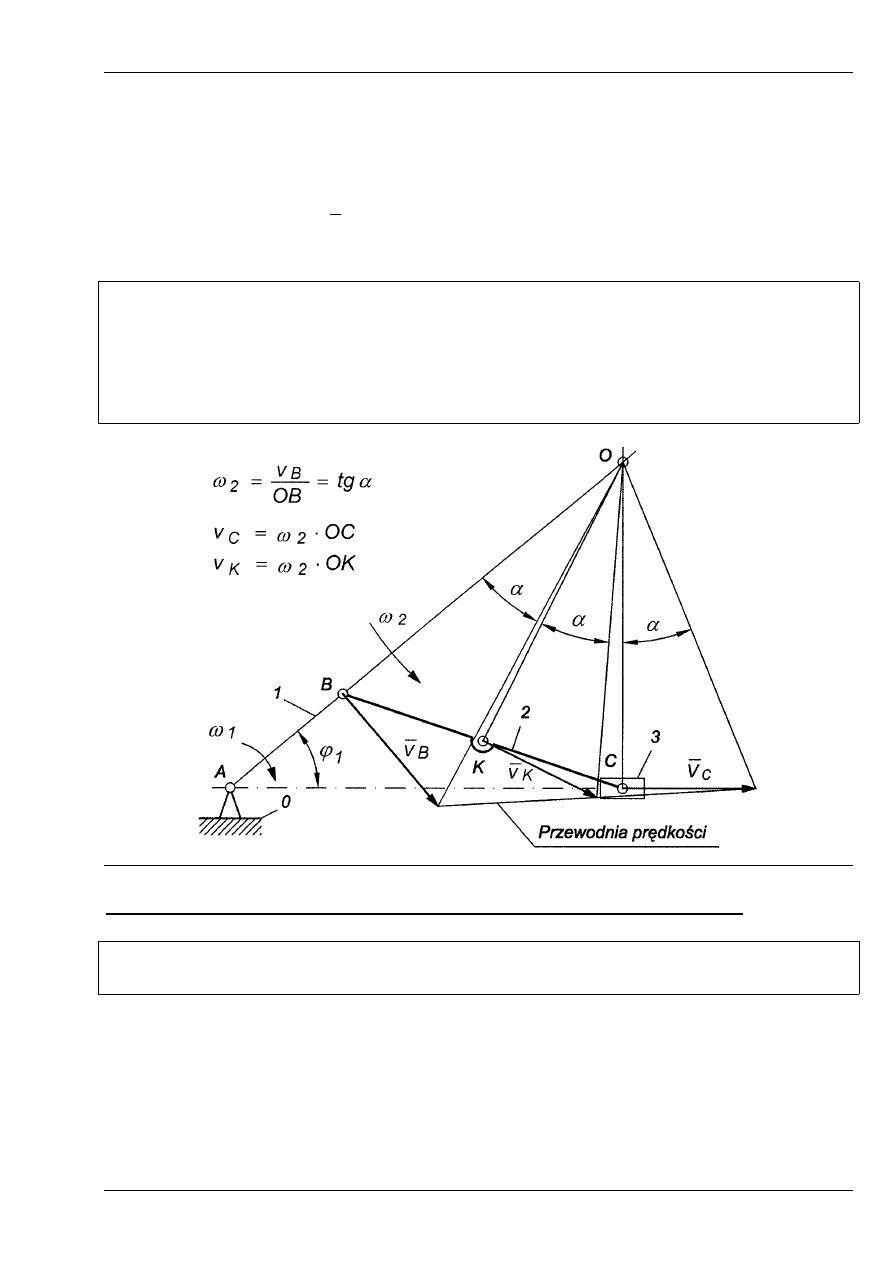
Przykład 3.
Dane: prędkość punktu B -
B
v
, oraz kierunek prędkości punktu C.
Należy wyznaczyć wartość prędkości punktu C należącego członu 2, który wykonuje ruch
płaski.
W celu wyznaczenia chwilowego środka obrotu członu 2 rysujemy prostą prostopadłą
do wektora prędkości punktu B w jego początku oraz analogicznie rysujemy prostą
prostopadłą do wektora prędkości punktu C. Na przecięciu obydwu prostych znajdu-
jemy punkt O stanowiący chwilowy środek obrotu członu 2. Następnie obliczamy
prędkość kątową
2
ω
. Znając prędkość kątową
2
ω
obliczamy prędkość dowolnego
punktu tego członu, np. punktu C i K.
AB
v
1
B
ω
=
Rys. 6
Wyznaczanie prędkości i przyspieszeń metodą grafoanalityczną nazywanej
również metodą planów prędkości i przyspieszeń lub metodą superpozycji
Prędkości i przyspieszenia punktów członów mechanizmów są wy-
znaczane na podstawie składania ruchu unoszenia i ruchu względnego
Metoda planów prędkości i przyspieszeń jest metodą grafoanalityczną, co
oznacza, że niektóre wielkości (prędkości i przyspieszenia liniowe i oraz pręd-
kości i przyspieszenia kątowe) obliczamy z równań algebraicznych a pozostałe
prędkości i przyspieszenia liniowe wyznaczamy z równań wektorowych.
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 5
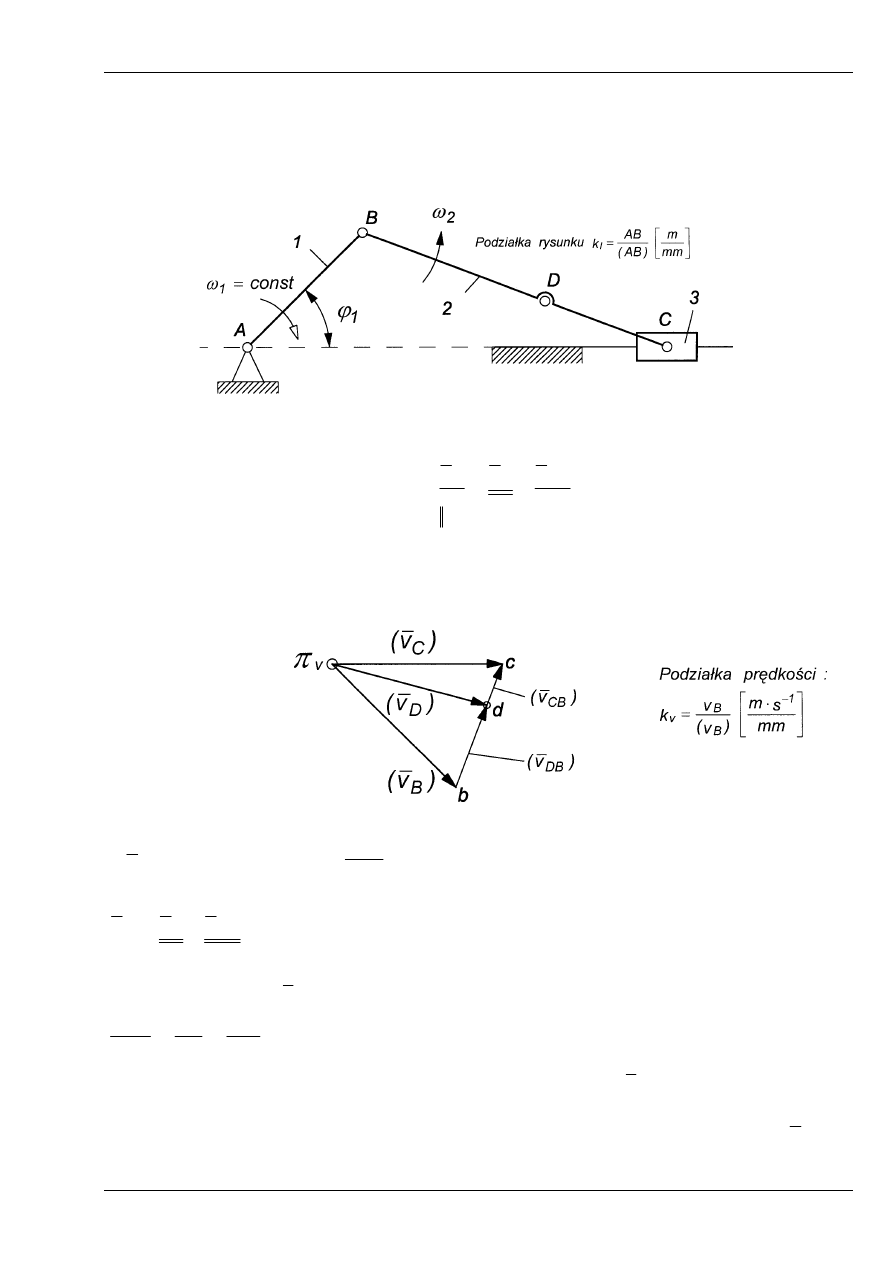
Przykład 4
Wyznaczyć prędkość i przyspieszenie punktów B, C, D mechanizmu korbowo-suwakowego
grafoanalityczną metodą planów.
Dane:
const
1
=
ω
, wymiary mechanizmu AB, BC, BD.
Zadanie rozwiązać dla zadanego położenia kątowego członu napędzającego
ϕ
1.
Rys. 7
Równania planu prędkości
Obliczamy:
AB
v
1
B
⋅
= ω
,
następnie piszemy równanie wektorowe:
BC
AB
AC
CB
B
C
v
v
v
⊥
⊥
+
=
(P4.1)
Przyjmujemy punkt biegunowy
π
v
i rozwiązujemy wykreślnie w podziałce równanie (1), ry-
sując tzw. plan prędkości, (rys. 8). Z planu prędkości otrzymamy wartość prędkości:
v
,
v
B
C
C
Rys. 8
Prędkość kątową dźwigni 2 obliczymy po odczytaniu z planu prędkości wartości wekto-
ra
v
CB
(odcinek bc
) :
CB
v
CB
2
=
ω
;
W celu wyznaczenia prędkości punktu D napiszemy równania:
DB
v
v
v
v
2
DB
DB
B
D
⋅
=
+
=
ω
(P4.2)
Prędkość względną - v
DB
można również wyznaczyć korzystając z proporcji:
DB
CB
db
cb
v
v
DB
CB
=
=
następnie należy zaznaczyć na planie punkt „d” (koniec wektora v
DB
).
Po połączeniu bieguna
π
v
z punktem ”d” z otrzymamy wektor prędkości punktu D tj.
v
D
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 6
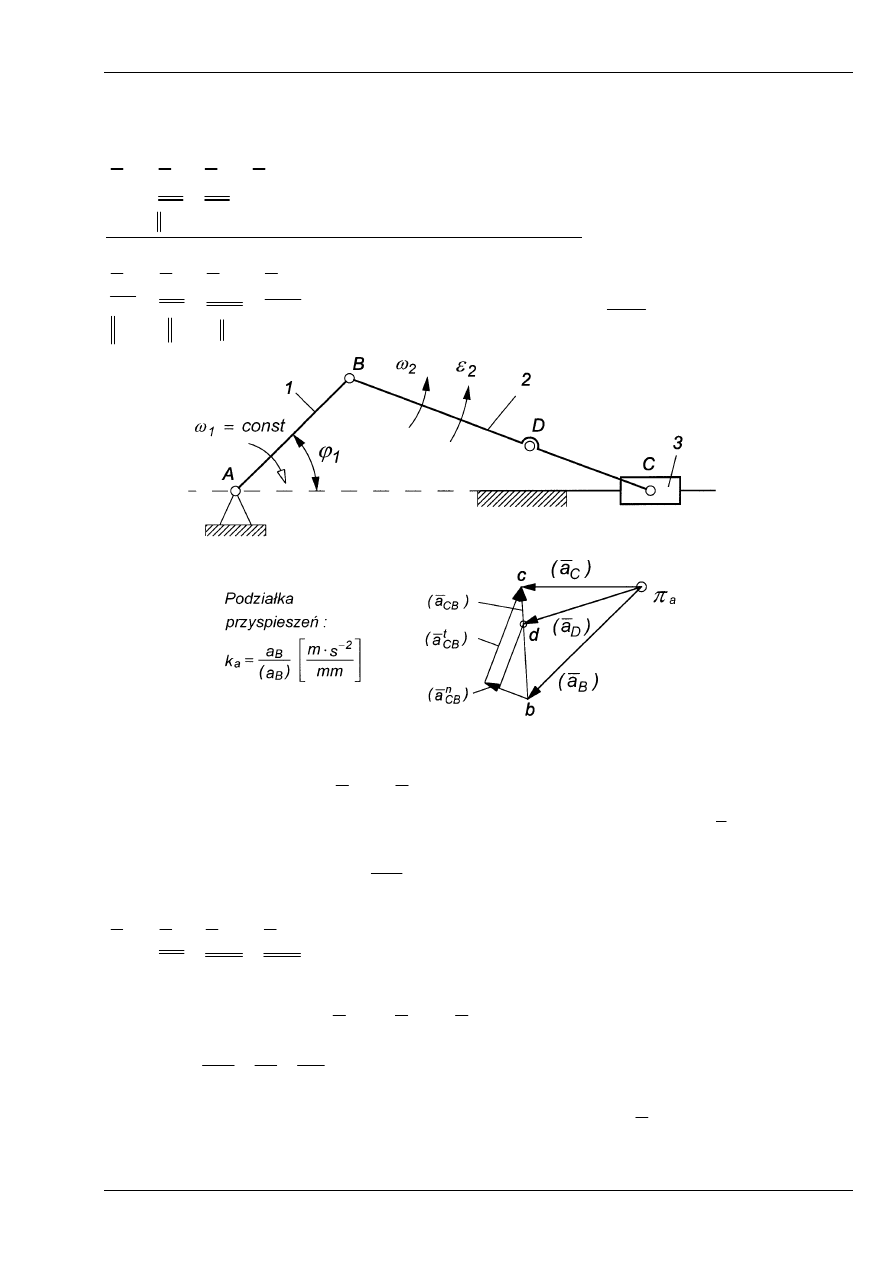
Równania planu przyspieszeń:
Równania przyspieszeń piszemy podobnie jak równania prędkości.
AB
1
t
B
n
B
t
B
n
B
B
0
ponieważ
0
a
a
a
a
a
=
=
=
+
=
ε
CB
CB
AB
AC
t
CB
n
CB
B
C
a
a
a
a
⊥
+
+
=
(P4.3)
gdzie:
CB
CB
v
a
2
2
2
CB
n
CB
⋅
=
=
ω
Rys. 9
Rozwiązujemy wykreślnie w podziałce równanie (3), rysując tzw. plan przyspieszeń
z dowolnie przyjętego bieguna
π
a
(rys. 9),
Otrzymamy przyspieszenia:
a
i
a
t
CB
C
Przyspieszenie kątowe dźwigni 2 obliczymy po odczytaniu wartości wektora a
t
CB
z planu
przyspieszeń (odcinek bc):
CB
a
t
CB
2
=
ε
.
Następnie znajdziemy przyspieszenie punktu D na podstawie równań:
DB
a
oraz
,
DB
a
:
gdzie
a
a
a
a
2
2
n
DB
2
t
DB
t
DB
n
DB
B
D
⋅
=
⋅
=
+
+
=
ω
ε
(P4.4)
Przyspieszenie względne -
a
a
a
t
DB
n
DB
DB
+
=
, można też wyznaczyć korzystając
z proporcji:
DB
CB
db
cb
a
a
DB
CB
=
=
.
Wyznaczając w ten sposób położenie punktu „d” na planie przyspieszeń i łącząc następnie
biegun
π
a
z tym punktem znajdziemy wykreślnie przyspieszenie
a
D .
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 7
Analiza kinematyczna mechanizmów dźwigniowych metodą wieloboku
wektorowego
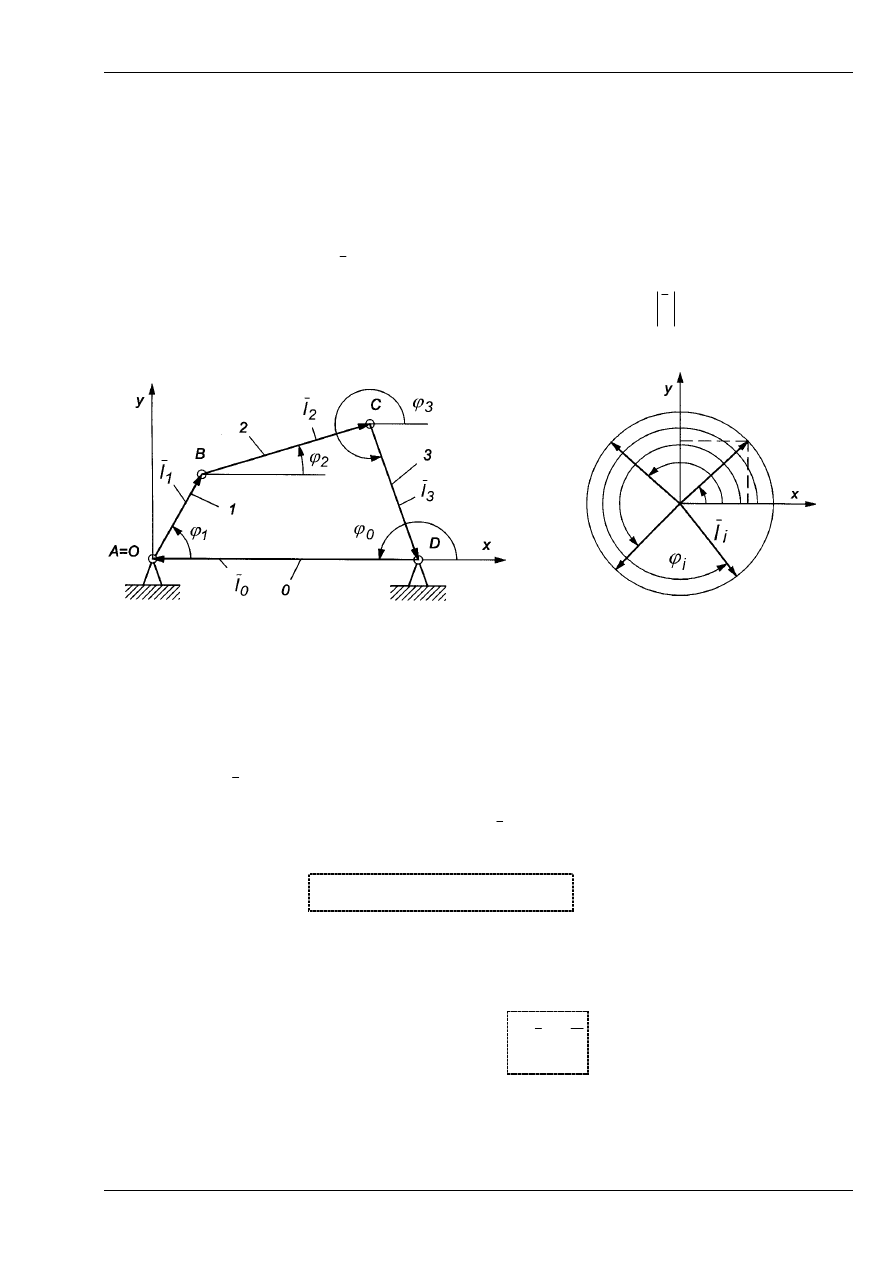
W opisywanej metodzie łańcuch kinematyczny dowolnego płaskiego me-
chanizmu dźwigniowego przedstawia się w postaci zamkniętego wieloboku
wektorowego (Rys. 10), który określa chwilowe położenie członów.
Każdy z wektorów
i
I
tego wieloboku zdefiniowany jest we współrzędnych
biegunowych przez dwa parametry: długość wektora
i
i
I
I
=
oraz kąt
i
ϕ
określający jego kierunek.
Rys. 10. Mechanizm dźwigniowy Rys. 11. Określanie kątów w metodzie
jako wielobok wektorowy wieloboku wektorowego
Dodatni kąt
i
ϕ
jest to taki kąt o jaki należy obrócić oś x układu współrzęd-
nych Oxy w kierunku przeciwnym do ruchu wskazówek zegara w prawoskręt-
nym układzie współrzędnych aby jej dodatni zwrot pokrył się z dodatnim zwro-
tem wektora
i
I co przedstawiono na Rys. 11.
Przy takiej umowie współrzędne wektora
)
I
,
I
(
I
iy
ix
i
wynoszą zawsze:
i
i
iy
i
i
ix
sin
I
I
,
cos
I
I
ϕ
ϕ
=
=
(1)
a znaki współrzędnych są określone poprzez znaki funkcji
ϕ
i
sin
i
ϕ
i
cos
.
Mechanizm płaski zdefiniowany jest przez zamknięty wielobok składający się
z n wektorów, co zapisujemy następująco:
0
I
n
1
i
i
=
∑
=
(2)
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 8
Wielobok wektorowy zbudowany na
członach mechanizmu posiada
2
⋅⋅⋅⋅
n
parametrów.
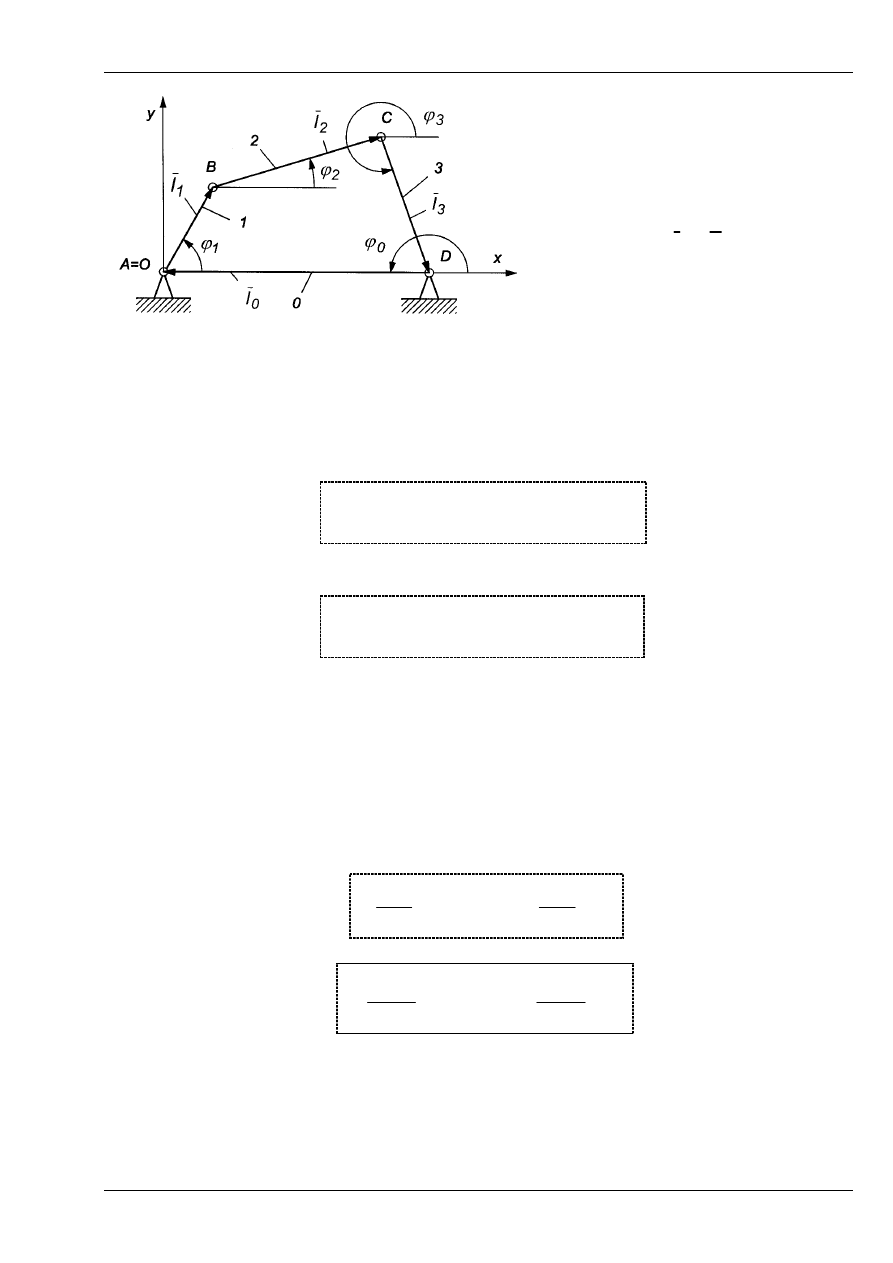
(2)
Rys. 10 powtórzony. Mechanizm dźwigniowy jako wielobok wektorowy
Wielobok wektorowy opisany równaniem (2) po zrzutowaniu go na osie pła-
skiego układu współrzędnych odpowiada dwóm równaniom skalarnym:
0
cos
l
,
0
l
i
n
1
i
i
n
1
i
ix
=
∑
⇒
=
∑
=
=
ϕ
(3)
0
sin
l
,
0
l
i
n
1
i
i
n
1
i
iy
=
∑
⇒
=
∑
=
=
ϕ
(4)
Ponieważ układ równań (3), (4) musi być oznaczony, na jego podstawie
można wyznaczyć dwa szukane parametry geometryczne np. dwie długo-
ści, długość i kąt lub dwa kąty. Pozostałe 2n - 2 parametry muszą być zatem
znane i należy je przyjąć jako dane w momencie definiowania mechanizmu.
Po zróżniczkowaniu równań (3), (4) względem czasu otrzymujemy układy
równań:
0
dt
dl
,
0
dt
dl
n
1
i
iy
n
1
i
ix
=
∑
=
∑
=
=
(5)
oraz
0
dt
l
d
,
0
dt
l
d
n
1
i
2
iy
2
n
1
i
2
ix
2
=
∑
=
∑
=
=
(6)
Z układu równań (5) wyznacza się dwie szukane prędkości liniowe lub kątowe
a na podstawie (6) dwa szukane przyspieszenia liniowe lub kątowe.
0
I
n
1
i
i
=
∑
=
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 9
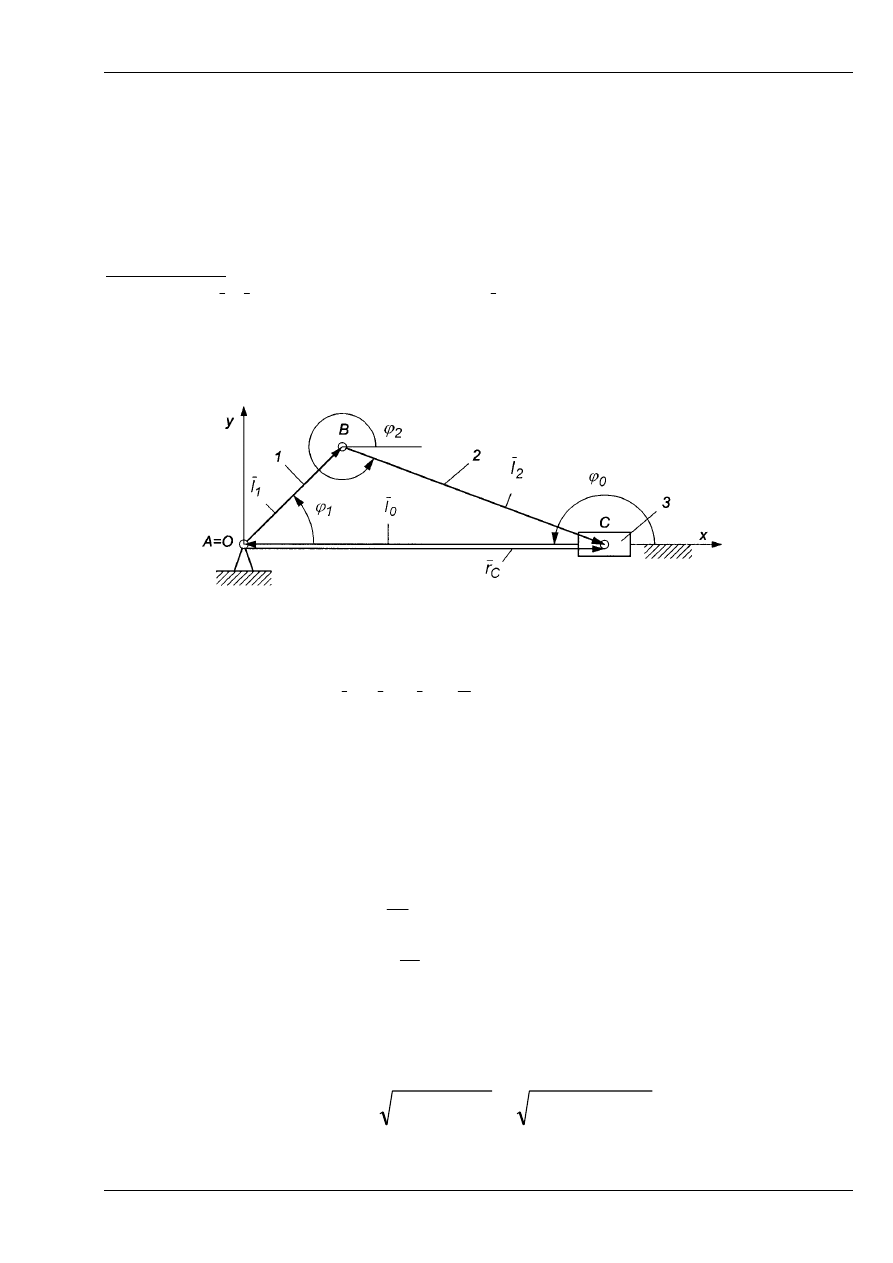
Przykład 5. Mechanizm korbowo-suwakowy
Mechanizm można zapisać trzema wektorami w sposób pokazany na Rys. 3. Należy zatem
przyjąć 2
⋅
3 – 2 = 4 parametry.
Dane:
π
ϕ
ϕ
ϕ
=
=
0
1
1
),
t
(
,
2
1
l
BC
,
l
AB
=
=
Szukane:
)
t
(
),
t
(
x
x
2
2
C
C
ϕ
ϕ =
=
,
)
t
(
),
t
(
v
v
2
2
C
C
ω
ω =
=
,
)
t
(
),
t
(
a
a
2
2
C
C
ε
ε =
=
Rozwiązanie
Dwa wektory
2
1
l
,
l
mają stałą długość. Wektor
0
l
zmienia swoją długość w czasie ruchu
mechanizmu. Wpisujemy wielobok wektorowy w kontur mechanizmu i oznaczamy położenia
kątowe poszczególnych wektorów względem osi Ox za pomocą kątów skierowanych.
Rys. 12
Opisujemy wielobok wektorowy równaniem wektorowym:
0
l
l
l
0
2
1
=
+
+
(P5.1)
Następnie piszemy odpowiednie równania skalarne:
0
l
cos
l
cos
l
0
2
2
1
1
=
−
+
ϕ
ϕ
(P5.2)
0
sin
l
sin
l
2
2
1
1
=
+
ϕ
ϕ
(P5.3)
Przyjmując oznaczenie mamy z (P5.3) mamy:
ϕ
λ
ϕ
ϕ
1
1
2
1
2
sin
sin
l
l
sin
−
=
−
=
P5.4)
i stąd
)
sin
sin(
arc
1
2
ϕ
λ
ϕ
−
=
(P5.5)
Dalej oznaczymy:
1
2
2
2
2
2
sin
1
sin
1
cos
A
ϕ
λ
ϕ
ϕ
−
=
−
=
=
(P5.6)
2
1
l
l
=
λ
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 10
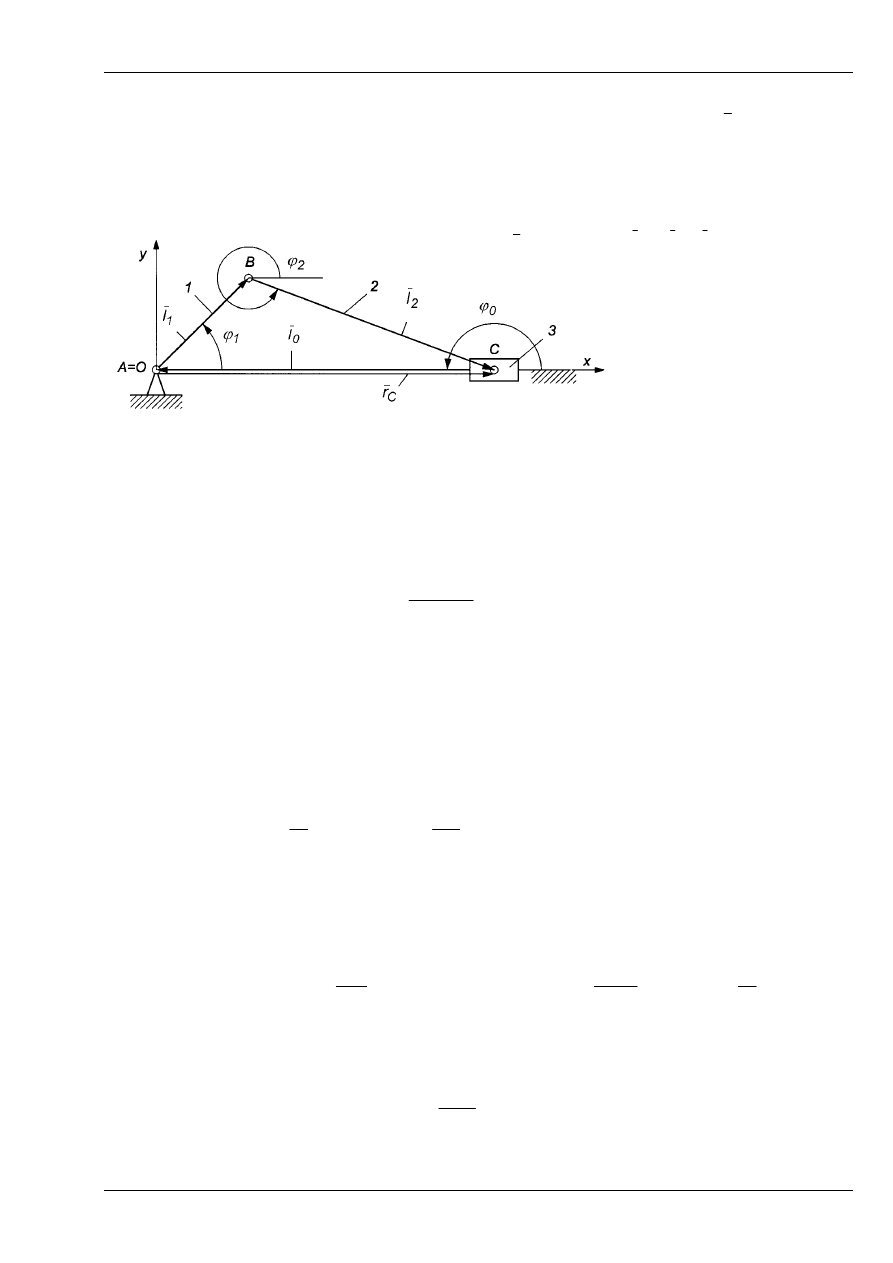
W celu wyznaczenia prędkości liniowej oraz przyspieszenia liniowego punktu C ko-
nieczne jest wprowadzenie wektora promienia wodzącego tego punktu
C
r
.
Wektor promień wodzący dowolnego mechanizmu płaskiego lub przestrzen-
nego prowadzony jest zawsze od początku układu współrzędnych do danego
punktu, którego prędkość lub przyspieszenie chcemy obliczyć.
2
1
0
C
C
l
l
l
)
0
,
x
(
r
+
=
−
=
(P5.7)
Rys. 12 powtórzony
Współrzędna wektora promienia wodzącego określająca położenie
suwaka wynosi:
A
l
cos
l
cos
l
cos
l
l
l
x
2
1
1
2
2
1
1
x
2
x
1
C
⋅
+
=
+
=
+
=
ϕ
ϕ
ϕ
P5.8)
W celu obliczenia prędkości kątowej różniczkujemy (P5.5) względem czasu:
1
1
1
2
1
1
2
2
1
1
2
2
cos
A
cos
cos
cos
cos
ϕ
ϕ
λ
ϕ
ϕ
ϕ
λ
ϕ
ω
ϕ
ϕ
λ
ϕ
ϕ
−
−
=
−
=
=
−
=
&
&
&
&
&
(
P5.9)
Następnie różniczkując (P1.8) względem czasu obliczymy prędkość liniową punktu C:
)
2
sin
A
5
,
0
(sin
l
x
v
1
1
1
1
1
C
C
ϕ
λ
ϕ
ϕ
−
+
−
=
=
&
&
(P5.10)
W celu obliczenia przyspieszenia kątowego różniczkujemy (P5.9) względem czasu:
−
−
=
=
1
1
1
1
2
1
2
1
2
2
cos
2
sin
cos
A
sin
A
ϕ
ϕ
ϕ
ϕ
λ
ϕ
ϕ
λ
ϕ
ε
&&
&
&&
(P5.11)
Następnie różniczkujemy (P5.10) i otrzymamy przyspieszenie liniowe punktu C: (P5.12)
+
+
−
+
−
=
=
1
1
2
3
3
1
2
1
1
1
1
1
1
C
C
2
cos
A
2
sin
A
4
cos
l
2
sin
A
2
sin
l
x
a
ϕ
λ
ϕ
λ
ϕ
ϕ
ϕ
λ
ϕ
ϕ
&
&&
&&
Jeżeli korba
1
I
AB
=
obraca się ze stałą prędkością kątową, wtedy jej przyspieszenie
kątowe jest równe zero czyli
0
dt
d
1
1
1
=
=
=
ω
ε
ϕ
&&
, co należy uwzględnić w równaniach.
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 11
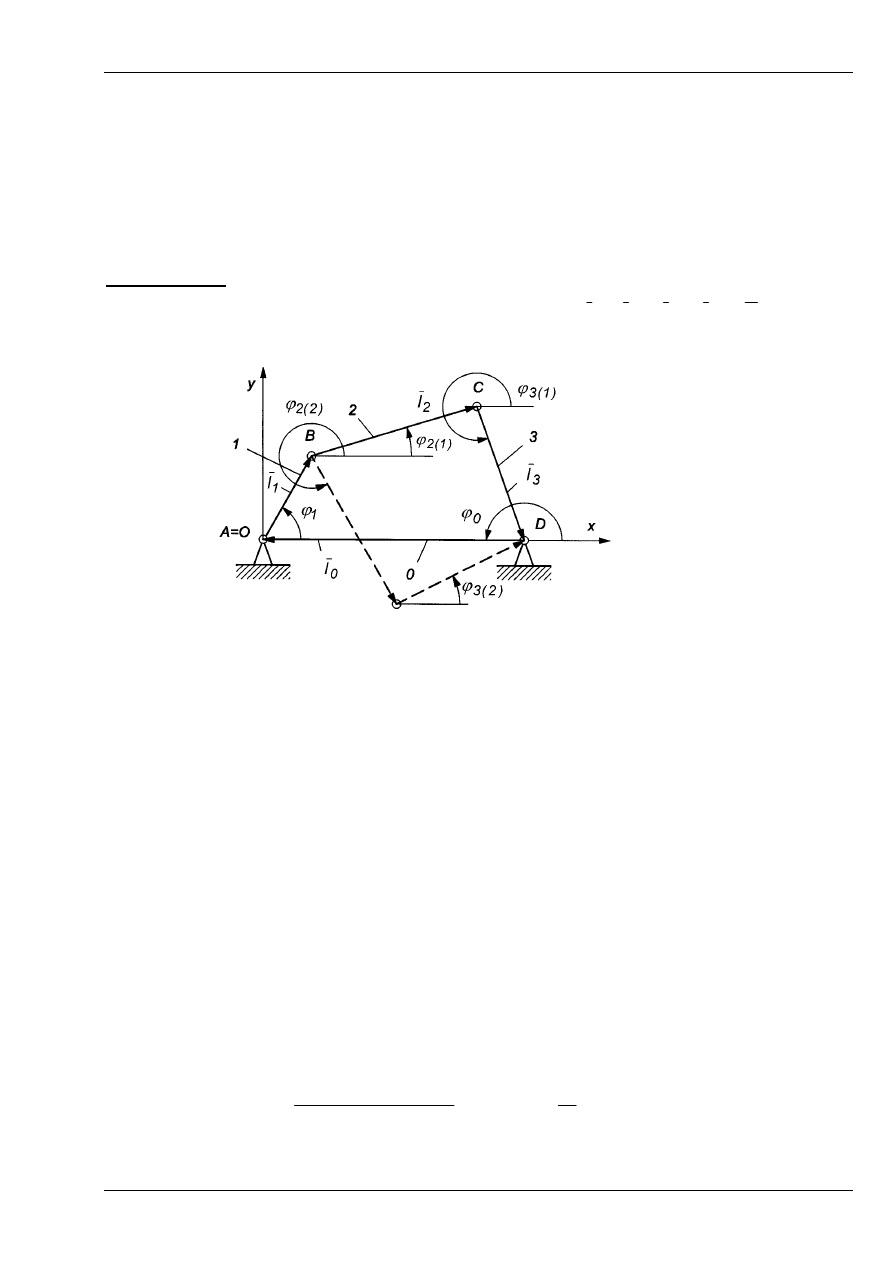
Przykład 6. Mechanizm czworoboku przegubowego
W ten mechanizm wpisujemy cztery wektory (Rys. 13). Należy zatem przyjąć 2
⋅
4 – 2 = 6
parametrów. Wszystkie wektory w przypadku tego mechanizmu mają stałą długość.
Dane:
π
ϕ
ϕ
=
0
0
3
2
1
1
,
l
,
l
,
l
,
l
,
Szukane:
3
2
3
2
3
2
,
,
,
,
,
ε
ε
ω
ω
ϕ
ϕ
.
Rozwiązanie
Mechanizm zapisujemy wielobokiem wektorowym:
0
l
l
l
l
0
3
2
1
=
+
+
+
(P6.1)
Rys. 13
Po rzutowaniu równania (P2.1) na osie układu współrzędnych otrzymamy:
0
sin
l
sin
l
sin
l
0
l
cos
l
cos
l
cos
l
3
3
2
2
1
1
0
3
3
2
2
1
1
=
+
+
=
−
+
+
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
(P6.2)
Przekształcamy układ równań (P2.2) do postaci:
3
3
2
2
1
1
3
3
0
2
2
1
1
sin
l
sin
l
sin
l
cos
l
l
cos
l
cos
l
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
−
=
+
−
=
−
+
(P6.3)
Po wprowadzeniu oznaczeń:
,
sin
l
B
,
l
cos
l
A
1
1
0
1
1
ϕ
ϕ
=
−
=
otrzymamy:
3
3
2
2
3
3
2
2
sin
l
sin
l
B
cos
l
cos
l
A
ϕ
ϕ
ϕ
ϕ
−
=
+
−
=
+
(P6.4)
Równania (P6.4) podnosimy do kwadratu i dodajemy stronami
0
l
l
sin
Bl
2
B
cos
Al
2
A
2
3
2
2
2
2
2
2
2
2
=
−
+
+
+
+
ϕ
ϕ
(P6.5)
Równanie (P6.5) dzielimy przez
2
Al
2
0
sin
A
B
cos
Al
2
l
l
B
A
2
2
2
2
3
2
2
2
2
=
+
+
−
+
+
ϕ
ϕ
(P6.6)
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 12
Przyjmiemy oznaczenia:
2
2
3
2
2
2
2
Al
2
l
l
B
A
C
−
+
+
=
,
A
B
D
=
,
zatem (P2.6) przyjmie postać:
0
sin
D
cos
C
2
2
=
+
+
ϕ
ϕ
(P6.7)
Po podniesieniu (P2.6) stronami do kwadratu otrzymujemy:
0
)
D
C
(
cos
C
2
cos
)
D
1
(
2
2
2
2
2
2
=
−
+
+
+
ϕ
ϕ
(P6.8)
Po podstawieniu
2
cos
w
ϕ
=
otrzymamy równanie kwadratowe w postaci:
0
)
D
C
(
Cw
2
w
)
D
1
(
2
2
2
2
=
−
+
+
+
(P6.9)
z którego wyznaczymy dwa pierwiastki
,
w
,
w
2
1
a następnie dwie wartości
kąta
2
ϕ
, tj. kąty
)
2
(
2
)
1
(
2
,
ϕ
ϕ
.
Dwa rozwiązania równania kwadratowego (P6.9) odpowiadają dwóm warian-
tom położenia członów mechanizmu czworoboku przegubowego przy ustalo-
nym położeniu członu napędzającego
1
ϕ
co pokazano na Rys. 13. Kąt
3
ϕ
znajdziemy z równania (P6.4). Otrzymamy odpowiednio:
)
2
(
3
)
1
(
3
,
ϕ
ϕ
.
W celu wyznaczenia prędkości kątowej członów 2 i 3 różniczkujemy pierwsze
z równań (P6.2) i otrzymujemy:
0
sin
l
sin
l
sin
l
3
3
3
2
2
2
1
1
1
=
+
+
ϕ
ω
ϕ
ω
ϕ
ω
(P6.10)
gdzie:
,
dt
d
,
dt
d
,
dt
d
3
3
2
2
1
1
ϕ
ω
ϕ
ω
ϕ
ω
=
=
=
- pochodne kątów,
W celu wyznaczenia prędkości kątowej
3
ω
obracamy układ współrzęd-
nych o kąt
2
ϕ
. Równanie (P6.10) przyjmie postać:
0
)
sin(
l
)
sin(
l
)
sin(
l
2
3
3
3
2
2
2
2
2
1
1
1
=
−
+
−
+
−
ϕ
ϕ
ω
ϕ
ϕ
ω
ϕ
ϕ
ω
(P6.11)
a ponieważ wyrażenie
0
)
sin(
l
2
2
2
2
=
−
ϕ
ϕ
ω
to otrzymamy:
)
sin(
l
)
sin(
l
2
3
3
2
1
1
1
3
ϕ
ϕ
ϕ
ϕ
ω
ω
−
−
−
=
(P6.12)
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 13
Analogicznie obracając układ współrzędnych o kąt
ϕ
3
mamy:
0
)
sin(
l
)
sin(
l
)
sin(
l
3
3
3
3
3
2
2
2
3
1
1
1
=
−
+
−
+
−
ϕ
ϕ
ω
ϕ
ϕ
ω
ϕ
ϕ
ω
(P6.13)
Ponieważ
0
)
sin(
3
3
=
−
ϕ
ϕ
to prędkość kątowa członu 2:
1
3
2
2
3
1
1
2
)
sin(
l
)
sin(
l
ω
ϕ
ϕ
ϕ
ϕ
ω
⋅
−
−
−
=
(P6.14)
W celu obliczenia przyspieszeń kątowych różniczkujemy równanie (P6.10)
0
sin
l
cos
l
sin
l
cos
l
sin
l
cos
l
3
3
3
3
3
2
3
2
2
2
2
2
2
2
1
1
1
1
1
2
1
=
+
+
+
+
+
ϕ
ε
ϕ
ω
ϕ
ε
ϕ
ω
ϕ
ε
ϕ
ω
(P6.15)
Przyspieszenie kątowe członu 3 -
3
ε
otrzymamy obracając układ współrzęd-
nych o kąt
ϕ
2
)
sin(
l
)
cos(
l
l
)
sin(
l
)
cos(
l
2
3
3
2
3
3
2
3
2
2
2
2
1
1
1
2
1
1
2
1
3
ϕ
ϕ
ϕ
ϕ
ω
ω
ϕ
ϕ
ε
ϕ
ϕ
ω
ε
−
−
+
+
−
+
−
−
=
(
P6.16)
Przyspieszenie kątowe członu 2 -
2
ε
otrzymamy obracając układ
współrzędnych o kąt
ϕ
3
)
sin(
l
l
)
cos(
l
)
sin(
l
)
cos(
l
3
2
2
3
2
3
3
2
2
2
2
3
1
1
1
3
1
1
2
1
2
ϕ
ϕ
ω
ϕ
ϕ
ω
ϕ
ϕ
ε
ϕ
ϕ
ω
ε
−
+
−
+
−
+
−
−
=
(P6.17)
Równania (P6.15), (P6.16) i (P6.17) ulegną uproszczeniu jeżeli prędkość
kątowa
const
1
=
ω
, wówczas przyspieszenie
0
1
=
ε
.
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 14
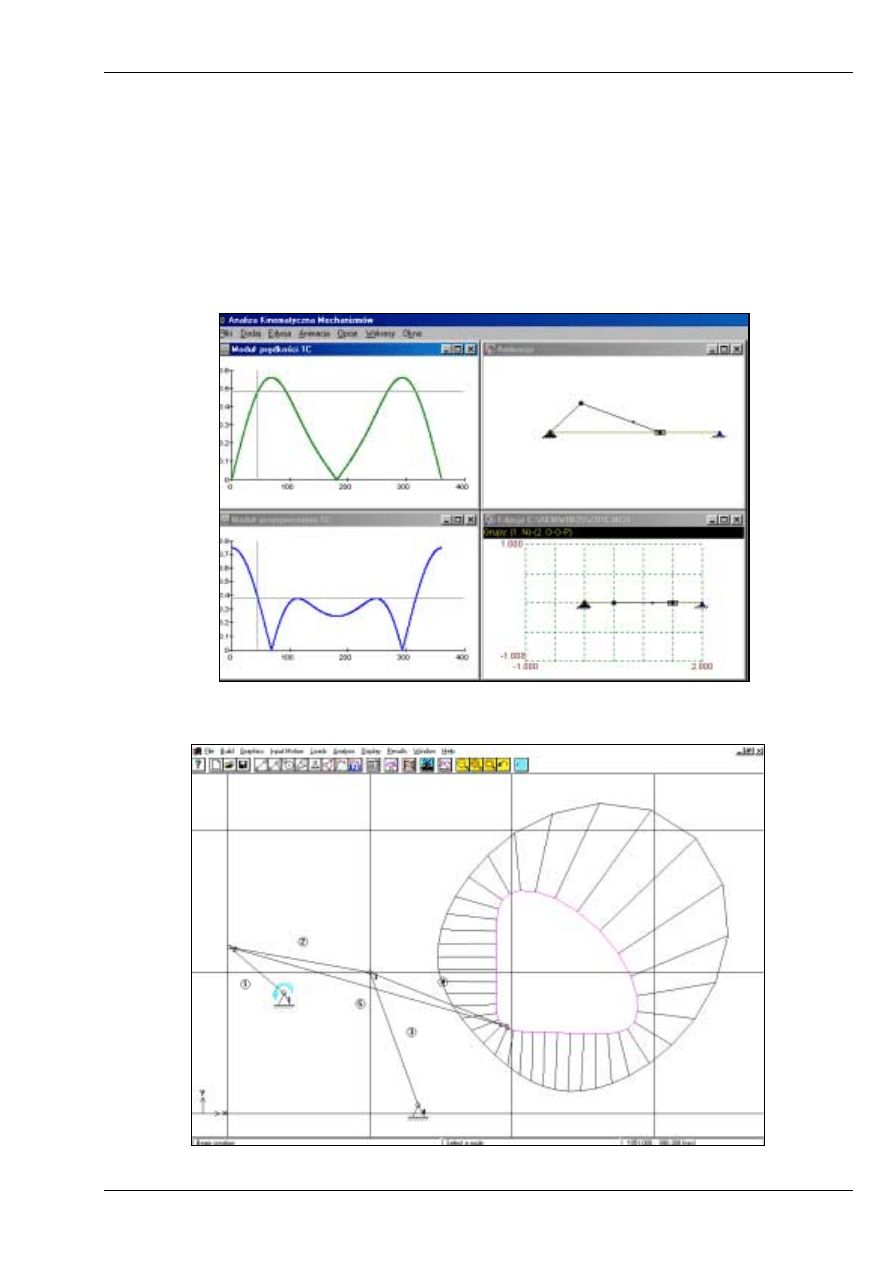
Wspomaganie komputerowe analizy kinematycznej mechanizmów
Programy:
1. Analiza kinematyczna mechanizmów – AKM WIN 2,53 (ga-
laxy.uci.agh.edu.pl\~kmtmipa)
2. Simulation and Analysis of Mechanisms – SAM 4.2 (www.artas.nl)
3. Working Model
AKM WIN 2,53: analiza kinematyczną płaskich mechanizmów dźwigniowych
i krzywkowych
SAM: Analiza kinematyczna i kinetostatyczna (siłowa) mechanizmów płaskich
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów
Opracowali: J. Felis, H. Jaworowski str. 15
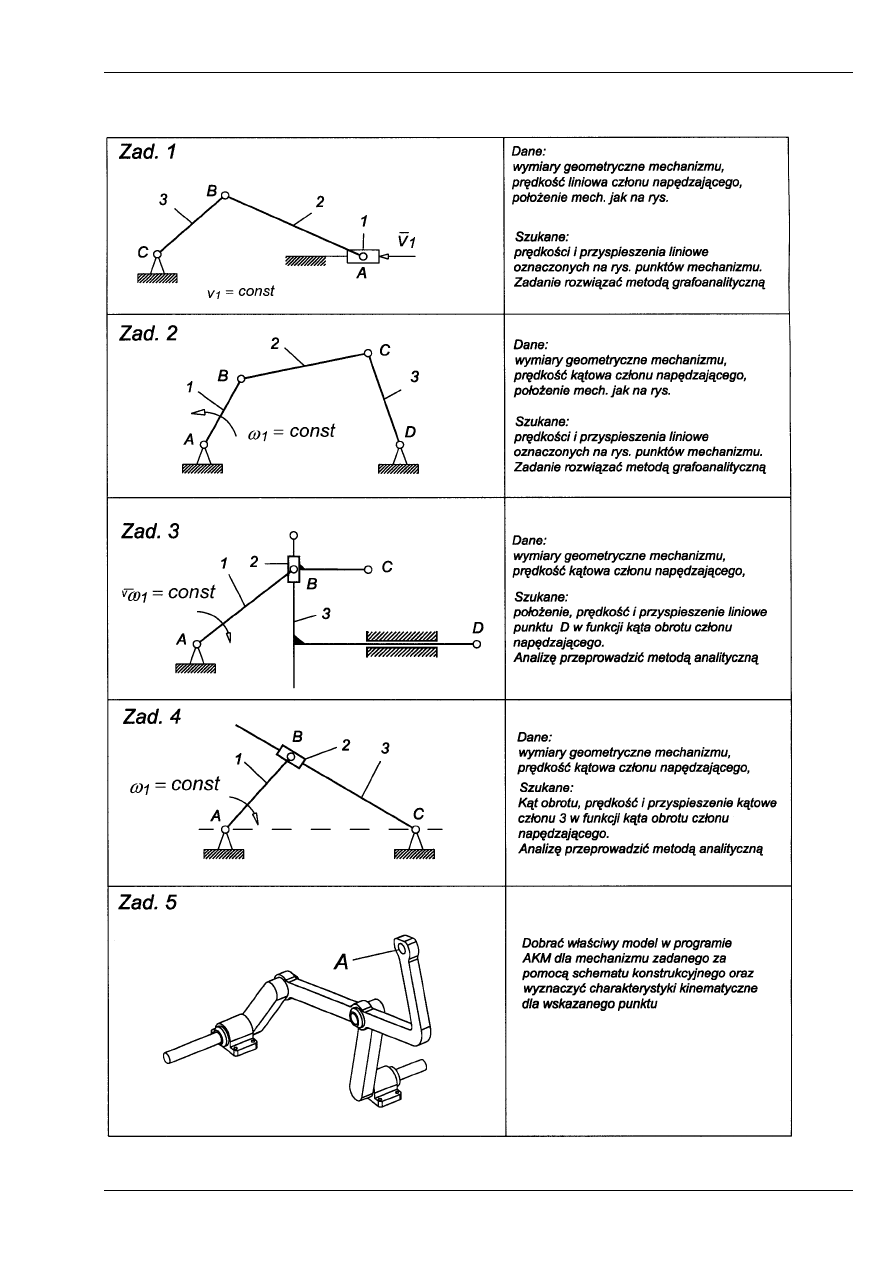
ZADANIA DO ROZWIĄZANIA NA ĆWICZENIACH
Mechanizm
można również
zamodelować w programie SAM