1
Kinematyka
(opis ruchu bez analizowania jego przyczyny)
Punkty materialne to obiekty obdarzone masą, których rozmiary
(objętość) możemy zaniedbać.
Pod pojęciem ruchu rozumiemy zmiany wzajemnego położenia
jednych ciał względem drugich wraz z upływem czasu.
Ruch odbywa się względem wybranego układu odniesienia.
Kinematyka – opis ruchu bez okre
ś
lania jego przyczyny
2
)]
(
),
(
),
(
[
t
z
t
y
t
x
=
(t)
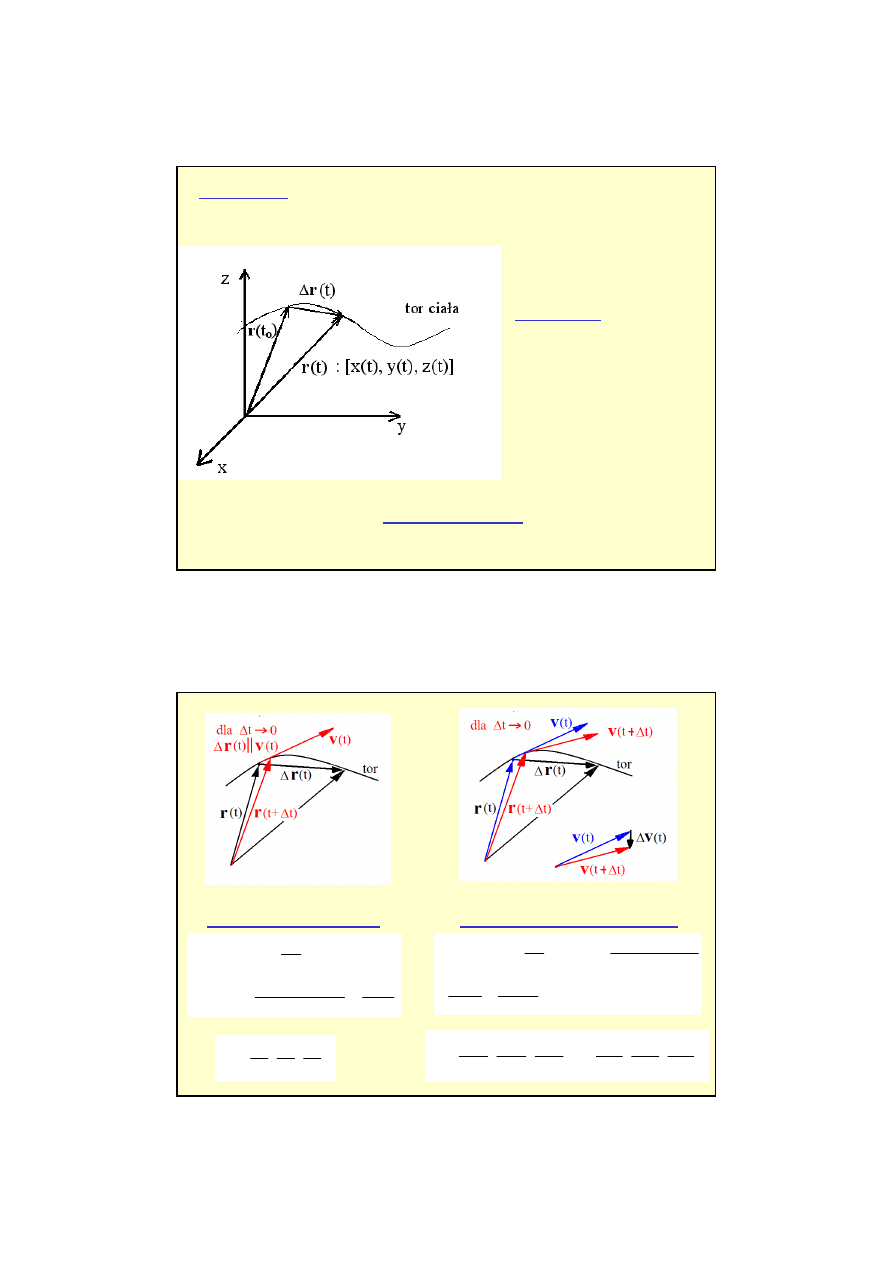
r
TOR RUCHU
)]
(
),
(
),
(
[
0
t
z
t
y
t
x
=
)
(t
(t)
(t)
∆
∆
∆
−
=
∆
r
r
r
PRZEMIESZCZENIE
Tor ruchu to krzywa jaką w przestrzeni zakreśla punkt materialny.
POŁO
Ż
ENIE
=
=
=
)
(
)
(
)
(
t
z
z
t
y
y
t
x
x
lub
kinematyczne
równania
ruchu
Układ kartezjański
PR
Ę
DKO
ŚĆ
CHWILOWA
dt
(t)
d
t
(t)
t)
(t
t
=
(t)
t
t
r
r
r
r
=
∆
−
∆
+
=
=
∆
∆
>
−
∆
>
−
∆
0
0
lim
lim
v
PRZYSPIESZENIE CHWILOWE
2
2
0
0
)
(
)
(
lim
lim
)
(
dt
t
d
dt
t
d
t
(t)
t)
(t
t
t
t
t
r
v
v
v
v
a
=
=
∆
−
∆
+
=
∆
∆
=
>
−
∆
>
−
∆
dt
dz
dt
dy
dt
dx
=
,
,
v
dt
z
d
dt
y
d
dt
x
d
dt
d
dt
d
dt
d
=
=
2
2
2
2
2
2
,
,
,
,
z
y
x
v
v
v
a
3
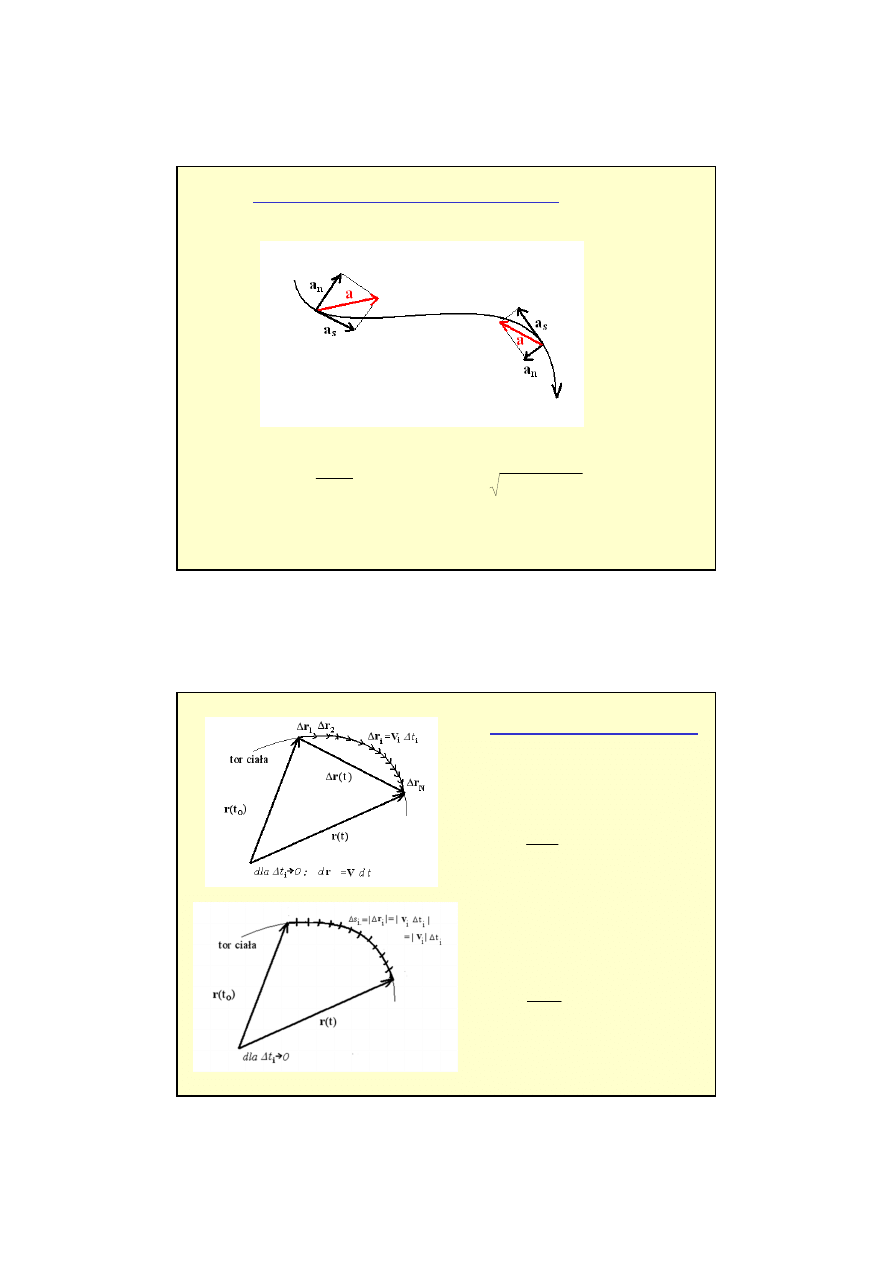
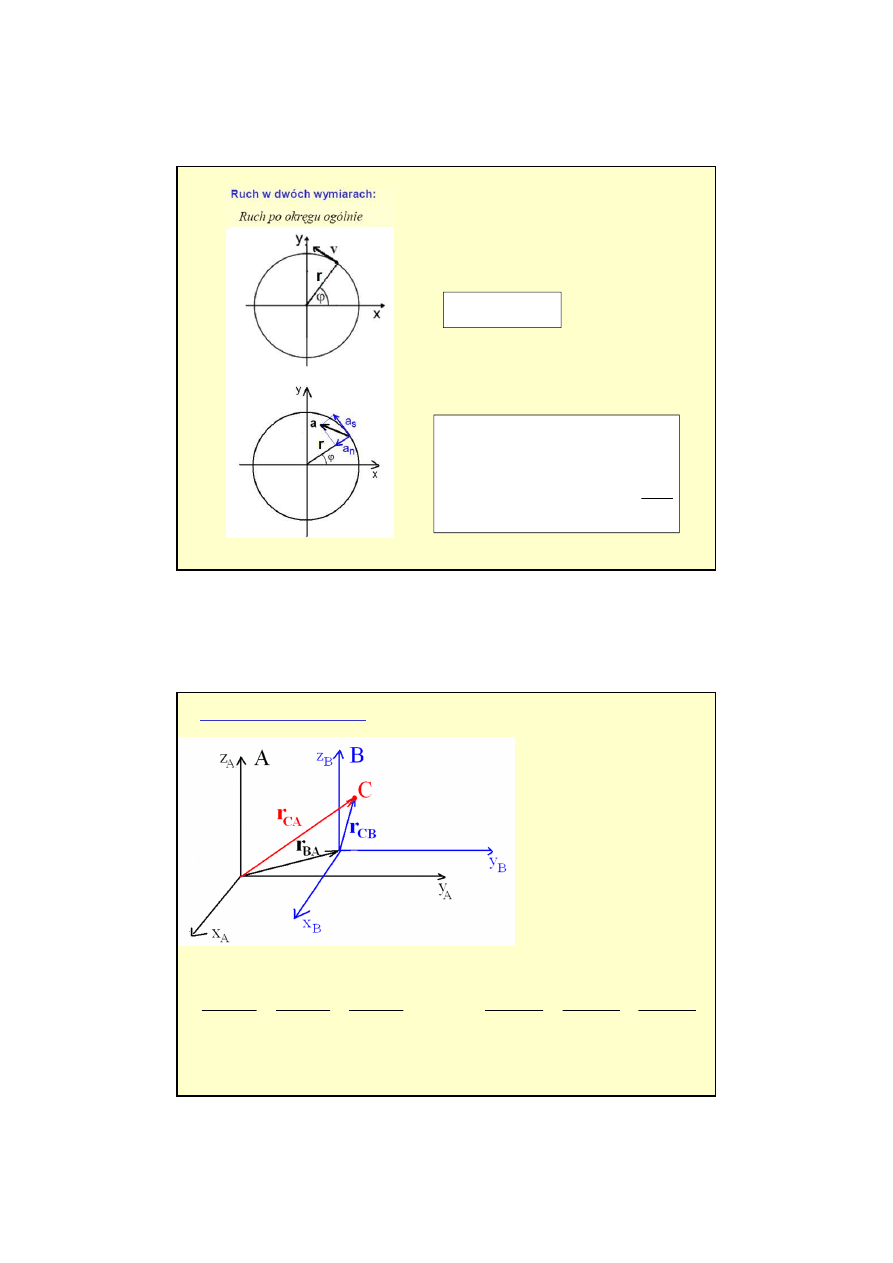
PRZYSPIESZENIE STYCZNE I NORMALNE
dt
t
d
t
a
s
)
(
)
(
v
=
)
(
)
(
)
(
2
2
t
a
t
a
t
a
s
n
−
=
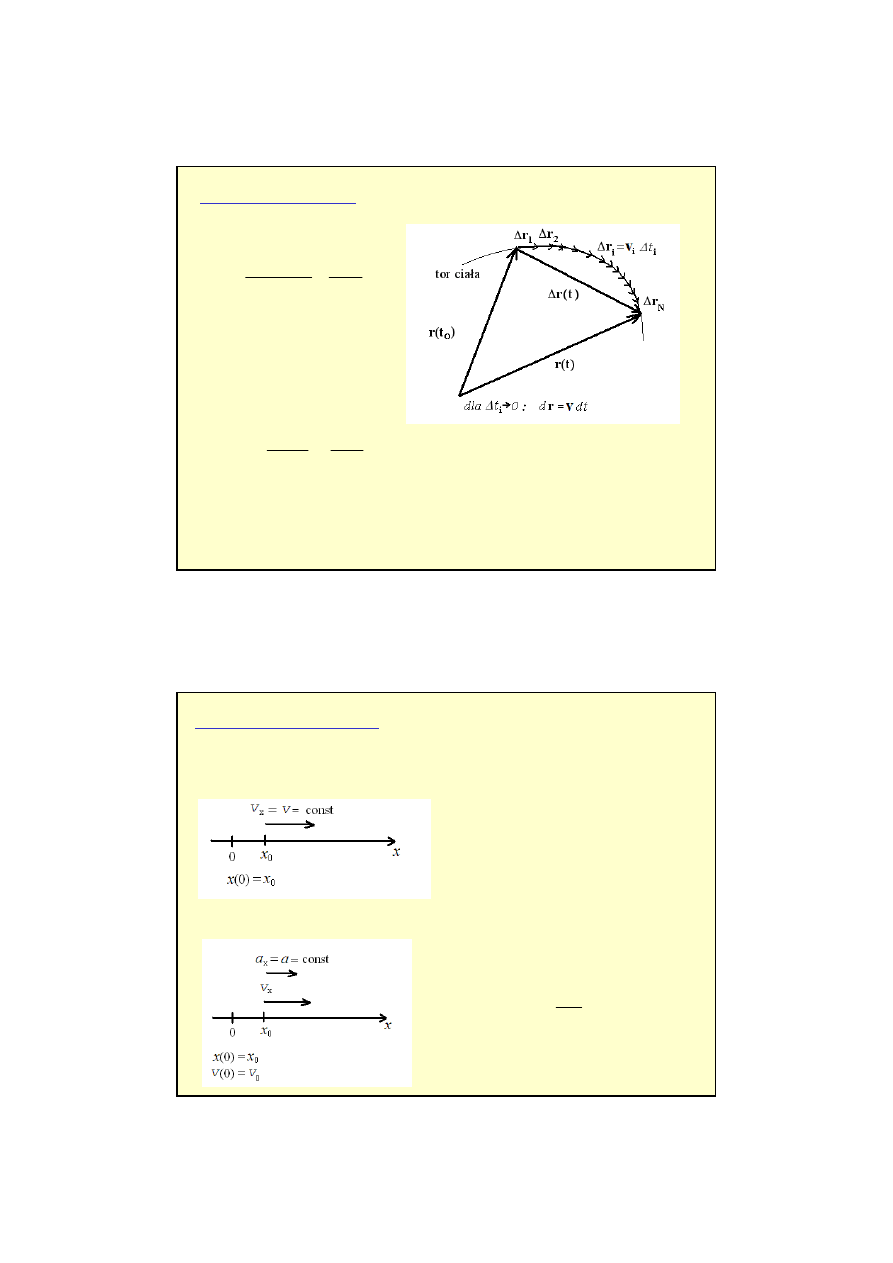
PRZEMIESZCZENIE I DROGA
∑
∑
∆
=
=
i
i
i
i
t
∆
s
t
s
i
v
)
(
dt
t
ds
t
)
(
)
(
=
v
Warto
ść
pr
ę
dko
ś
ci
to szybko
ść
(inaczej pr
ę
dko
ść
liniowa)
)
(
|
)
(
|
t
t
v
=
v
∑
∑
∆
=
=
i
i
i
t
∆
t
∆
i
i
v
r
r )
(
dt
(t)
d
=
(t)
r
v
4
PR
Ę
DKO
ŚĆ Ś
REDNIA
t
t
t
t
t
t
ś
r
∆
∆
=
−
−
=
)
(
)
(
)
(
0
0
r
r
r
v
Wektorowa:
t
t
s
t
t
t
s
ś
r
∆
=
−
=
)
(
)
(
)
(
0
v
Liniowa:
|
|
)
(
ś
r
ś
r
v
≠
v
Uwaga:
PRZYKŁADY RUCHU
Ruch w jednym wymiarze (y=0, z=0):
Ruch jednostajny prostoliniowy
const
x
=
=
v
v
Ruch jednostajnie zmienny prostoliniowy
const
a
a
x
=
=
t
x
x
v
+
=
0
równanie ruchu
t
a
+
=
0
v
v
x
2
2
0
0
at
t
x
x
+
+
=
v
równanie ruchu
UWAGA: v mo
ż
e by
ć
ujemne lub dodatnie
(od tego zale
ż
y, w któr
ą
strone ciało sie porusza)
UWAGA: v
0
,
a
mog
ą
by
ć
ujemne lub dodatnie. Gdy v
0
,
a
maj
ą
:
1) ten sam znak to ruch jest jednostajnie przyspieszony,
2) ró
ż
ne znaki to ruch jest jednostajnie opó
ź
niony.
5
Ruch w dwóch wymiarach (z=0):
−
=
=
=
=
g
g
a
g
a
y
y
x
x
0
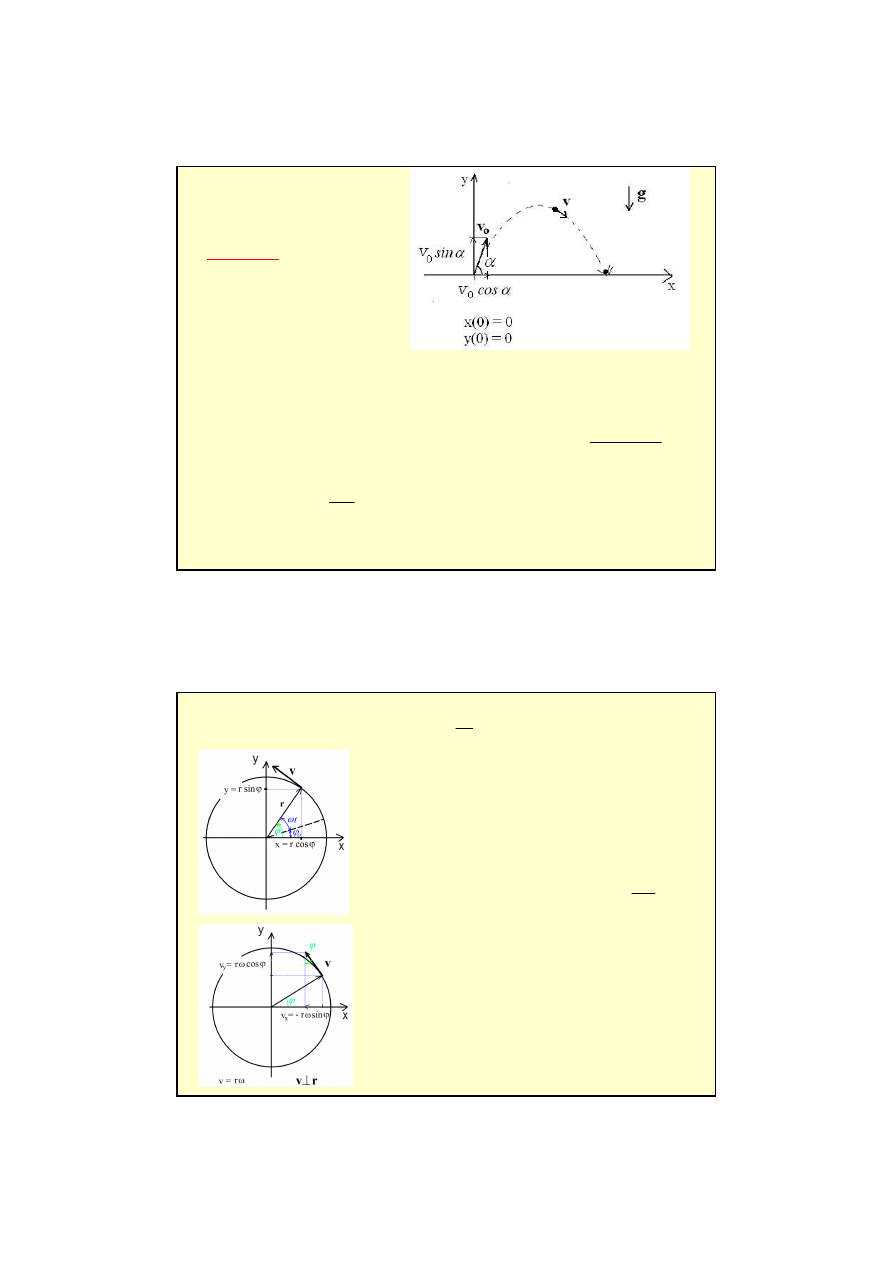
Rzut ukośny
−
=
=
gt
y
x
α
α
sin
cos
0
0
v
v
v
v
−
=
=
2
)
sin
(
)
cos
(
2
0
0
gt
t
y
t
x
α
α
v
v
równania
ruchu
2
2
0
)
cos
(
2
)
(
x
g
x
tg
y
α
α
v
−
=
równanie toru
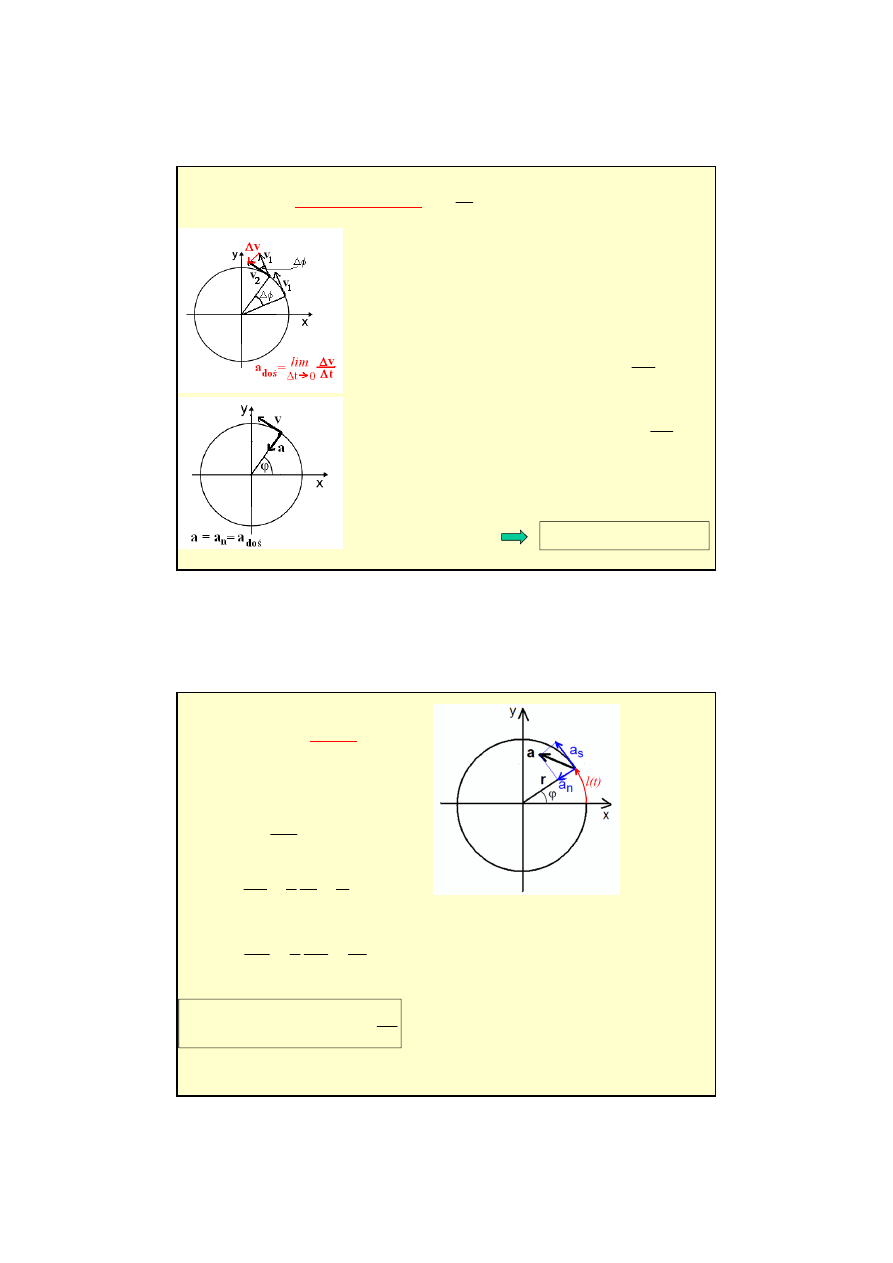
Ruch w dwóch wymiarach:
Ruch po okręgu – stała prędkość kątowa:
+
=
=
=
0
)
(
.
)
(
ϕ
ω
ϕ
t
t
const
r
t
r
+
=
+
=
)
sin(
)
(
)
cos(
)
(
0
0
ϕ
ω
ϕ
ω
t
r
t
y
t
r
t
x
+
=
=
+
−
=
=
)
cos(
/
)
sin(
/
0
0
ϕ
ω
ϕ
ω
t
rω
dt
dy
t
rω
dt
dx
y
x
v
v
const
dt
d
=
=
ϕ
ω
równania
ruchu
Układ kartezjański:
Układ biegunowy:
const
t
=
∆
∆
= ϕ
ω
6
Ruch w dwóch wymiarach:
Ruch po okręgu –
stała prędkość kątowa:
0
=
=
dt
d
ω
ε
−
=
+
−
=
=
−
=
+
−
=
=
2
0
2
2
0
2
)
sin(
/
)
cos(
/
yω
t
rω
dt
d
a
xω
t
rω
dt
d
a
y
y
x
x
ϕ
ω
ϕ
ω
v
v
Układ kartezjański:
Układ biegunowy:
2
,
0
rω
a
a
a
doś
n
S
=
=
=
r
a
2
2
2
)
,
(
ω
yω
xω
−
=
−
−
=
lub inaczej:
const
t
=
∆
∆
= ϕ
ω
+
=
=
=
0
)
(
.
)
(
ϕ
ω
ϕ
t
t
const
r
t
r
+
=
+
=
)
sin(
)
(
)
cos(
)
(
0
0
ϕ
ω
ϕ
ω
t
r
t
y
t
r
t
x
+
=
=
+
−
=
=
)
cos(
/
)
sin(
/
0
0
ϕ
ω
ϕ
ω
t
rω
dt
dy
t
rω
dt
dx
y
x
v
v
const
dt
d
=
=
ϕ
ω
równania
ruchu
Ruch w dwóch wymiarach:
Ruch po okręgu -
zmienny
=
=
=
r
t
l
t
const
t
r
)
(
)
(
0
oraz
.
)
(
0
ϕ
ϕ
r
t
l
r
t
v
=
=
=
d
d
1
d
d
ϕ
ω
Układ biegunowy:
r
a
t
r
t
s
=
=
=
d
d
1
d
d
v
ω
ε
r
r
a
a
ε
r
a
doś
n
S
2
2
,
v
=
=
=
=
ω
7
=
=
=
=
r
rω
a
a
ε
r
a
doś
n
S
2
2
v
rω
=
v
WZGL
Ę
DNO
ŚĆ
RUCHU
(t)
(t)
=
(t)
BA
CB
CA
r
r
r
+
Wzgl
ę
dne poło
ż
enie:
dt
(t)
d
dt
(t)
d
=
dt
(t)
d
BA
CB
CA
r
r
r
+
(t)
(t)
=
(t)
BA
CB
CA
v
v
v
+
Wzgl
ę
dna pr
ę
dko
ść
:
dt
(t)
d
dt
(t)
d
=
dt
(t)
d
BA
CB
CA
v
v
v
+
(t)
(t)
=
(t)
BA
CB
CA
a
a
a
+
Wzgl
ę
dne przyspieszenie:

8
Wyszukiwarka
Podobne podstrony:
3 kinematyka id 34358 Nieznany (2)
kinema1 id 234915 Nieznany
kinematykawyklad7 id 235023 Nieznany
lancuchy kinematyczne id 263224 Nieznany
kinematyka id 234982 Nieznany
IMIR przyklady kinematyka id 21 Nieznany
IMIC przyklady drgania id 21180 Nieznany
IMIC uklady nieinercjalne id 21 Nieznany
Kinematyka 2010 id 234998 Nieznany
IMIC przyklady prady id 211813 Nieznany
Kinemat punktu id 234923 Nieznany
Kinematyka odwrotna id 235013 Nieznany
Kinematyka 1D id 234997 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
więcej podobnych podstron