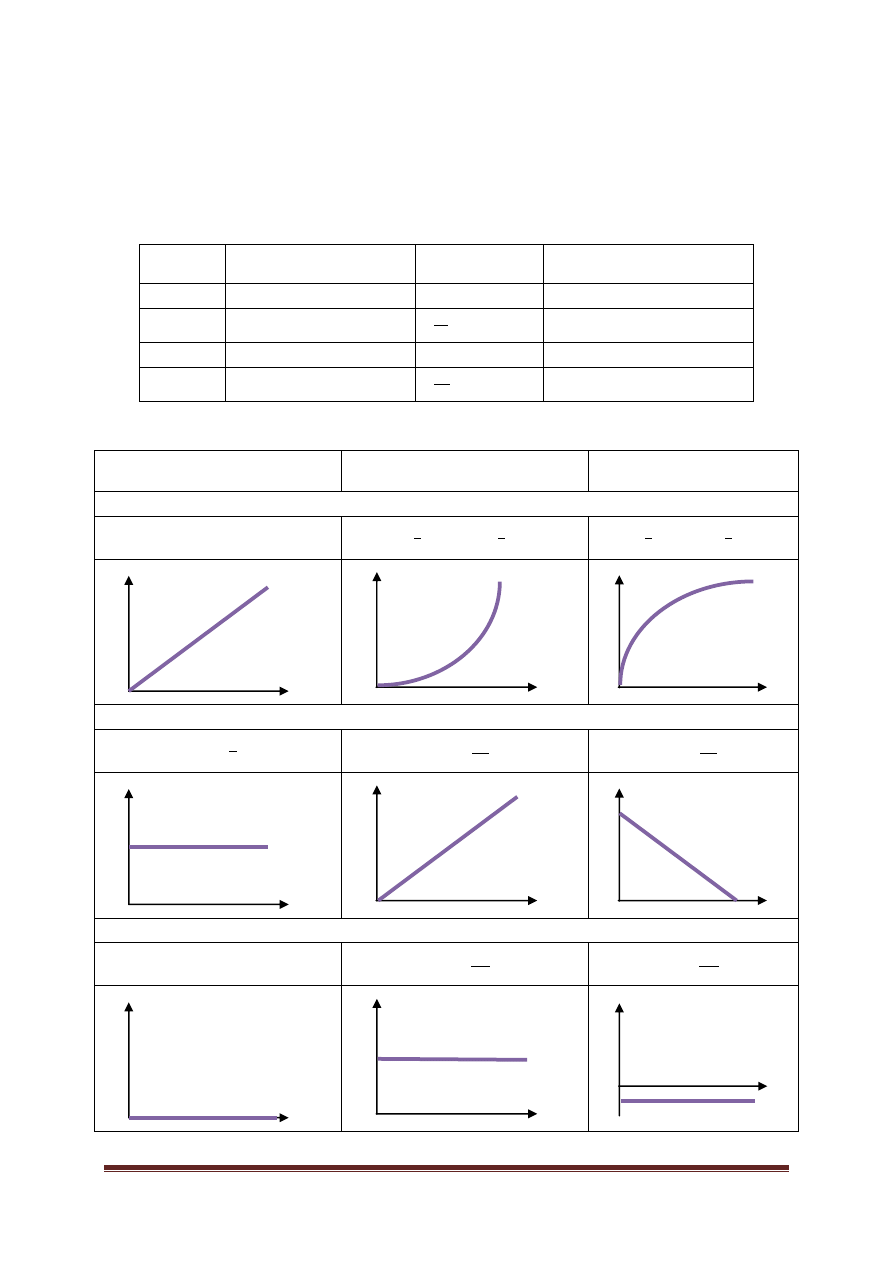
Ewa Mariola Lutkiewicz

Strona 1

ROZWIĄZANIE PRZYKŁADOWYCH ZADAŃ Z FIZYKI

Dział – „Kinematyka”

Realizowany w klasie pierwszej Gimnazjum nr 2 w Ełku

Przypomnienie podstawowych danych:

Wielkość
fizyczna

Nazwa

Jednostka

Jednostka słownie

s

Droga

1m

metr

v

Prędkość

1

𝑚

𝑠

metr na sekundę

t

Czas

1 s

sekunda

a

Przyspieszenie

1

𝑚

𝑠

2

metr na sekundę do kwadratu

Przypomnienie podstawowych wzorów i wykresów:

Ruch jednostajny

Ruch przyspieszony

Ruch opóźniony

1. Droga

𝑠 = 𝑣 ∙ 𝑡

𝑠 =

1
2

𝑣 ∙ 𝑡 , 𝑠 =

1
2

𝑎 ∙ 𝑡

2

𝑠 =

1
2

𝑣 ∙ 𝑡, 𝑠 =

1
2

𝑎 ∙ 𝑡

2

s

t

s



t

s



t

2. Prędkość

𝑣 =

𝑠

𝑡

𝑣 =

2𝑠

𝑡

𝑣 =

2𝑠

𝑡

v

t

v



t

v



t

3. Przyspieszenie

a=0

𝑎 =

∆𝑣

∆𝑡

𝑎 =

∆𝑣

∆𝑡

a

t

a



t

a



t

Ewa Mariola Lutkiewicz

Strona 2

Zadanie 1. Oblicz drogę jaką przebędzie ciało poruszające się z prędkością 20

km/h w czasie 3 godzin.

Dane:

Szukane:

s

m

h

km

v

9

5

5

20





s=?

s

s

h

t

10800

3600

3

3









Aby obliczyć drogę s dla tego ciała musimy najpierw zamienić jednostkę prędkości i jednostkę czasu. Obie
liczby z jednostkami dopisujemy do danych.

s

m

s

m

s

m

s

m

s

m

s

m

h

km

v

9

5

5

9

50

18

100

36

200

36

10

20

3600

1000

20

20



















Do dalszych obliczeń wygodniej jest wziąć wartość przedstawioną w ułamku.
Ponieważ ruch jest ruchem jednostajnym prostoliniowym stosujemy przekształcenie wzoru na prędkość.

Wzór:

t

s

v



stąd

t

v

s





Obliczenia:

km

m

m

s

s

m

t

v

s

60

60000

1200

50

10800

9

50

















Odp.: Ciało przebędzie drogę równą 60 km.

Zadanie 2. Oblicz jaką odległość przebędzie rower poruszający się z prędkością

20 m/s przez 2 godziny.

Dane:

Szukane:

s

m

v

20



s=?

s

s

h

t

7200

3600

2

2









Aby obliczyć drogę s dla tego ciała musimy najpierw zamienić jednostkę czasu. Liczbę z jednostkami
dopisujemy do danych.

Ponieważ ruch jest ruchem jednostajnym prostoliniowym stosujemy przekształcenie wzoru na prędkość.
Odległość traktujemy jako przebytą drogę.

Wzór:

stąd

Obliczenia:

km

m

s

s

m

t

v

s

4

,

14

14400

7200

20













Odp.: Rower przebędzie odległość równą 14,4 km.

t

s

v



t

v

s





Ewa Mariola Lutkiewicz

Strona 3

Zadanie 3. Rowerzysta przejechał pierwsze 5 km ze średnią prędkością 20

km/h a następnie 12 km ze średnią prędkością 16 km/h. Z jaką średnią
prędkością jechał rowerzysta na całej trasie i w jakim czasie ją przebył?
Dane:

Szukane:

km

s

5

1



?



śr

v

h

km

v

20

1



?



c

t

km

s

12

2



h

km

v

16

1



Ponieważ wszystkie jednostki są podane w kilometrach i godzinach nie trzeba ich zamieniać.
Aby obliczyć średnią prędkość rowerzysty musimy obliczyć całkowitą drogę przejechaną przez ten rower oraz
całkowity czas potrzebny na ten przejazd. Jest on również wielkością przez nas poszukiwaną.
Obliczamy całkowita drogę:

km

km

km

s

s

s

c

17

12

5

2

1











Aby obliczyć całkowity czas przejazdu musimy obliczyć czasy potrzebne na przejechanie poszczególnych
odcinków drogi.
Ponieważ ruch jest ruchem jednostajnym prostoliniowym stosujemy przekształcenie wzoru na prędkość.

Obliczamy czas przejazdu na drodze 5 km:
Wzór:

stąd

v

s

t



Obliczenia:

h

h

h

km

km

v

s

t

25

,

0

4

1

20

5

1

1

1









Obliczamy czas przejazdu na drodze 12 km:
Obliczenia:

h

h

h

km

km

v

s

t

75

,

0

4

3

16

12

2

2

2









Całkowity czas przejazdu:

h

h

h

t

t

t

c

1

75

,

0

25

,

0

2

1











Obliczamy średnią prędkość na całej trasie:

h

km

h

km

t

s

v

c

c

śr

17

1

17







Odp. Średnia prędkość rowerzysty wynosi

h

km

17

, a czas przejazdu zajął jedną

godzinę.

t

s

v



Ewa Mariola Lutkiewicz

Strona 4

Zadanie 4. Z jakim przyspieszeniem porusza się rowerzysta, jeżeli w ciągu 10

minut przebywa drogę równą 0,5 km?

Dane:

Szukane:

s

s

t

600

60

10

min

10









a=?

m

km

s

500

5

,

0





Aby obliczyć drogę s dla tego ciała musimy najpierw zamienić jednostkę czasu i jednostkę prędkości. Liczby z
jednostkami dopisujemy do danych.

Ponieważ ruch jest ruchem jednostajnie przyspieszonym prostoliniowym stosujemy wzór na przyspieszenie po
przekształceniu wzoru na drogę.

Wzór:

2

2

1

t

a

s







/

mnożymy obustronnie przez 2

2

2

t

a

s





/dzielimy obustronnie przez

2

t

a

t

s



2

2

/”odwracamy” wzór

2

2

t

s

a



Obliczenia:

Pamiętamy o podniesieniu do potęgi wartości czasu oraz jej jednostki





2

2

2

2

360

1

360000

1000

600

500

2

2

s

m

s

m

s

m

t

s

a











Odp. Rowerzysta porusza się z przyspieszeniem

2

360

1

s

m

Ewa Mariola Lutkiewicz

Strona 5

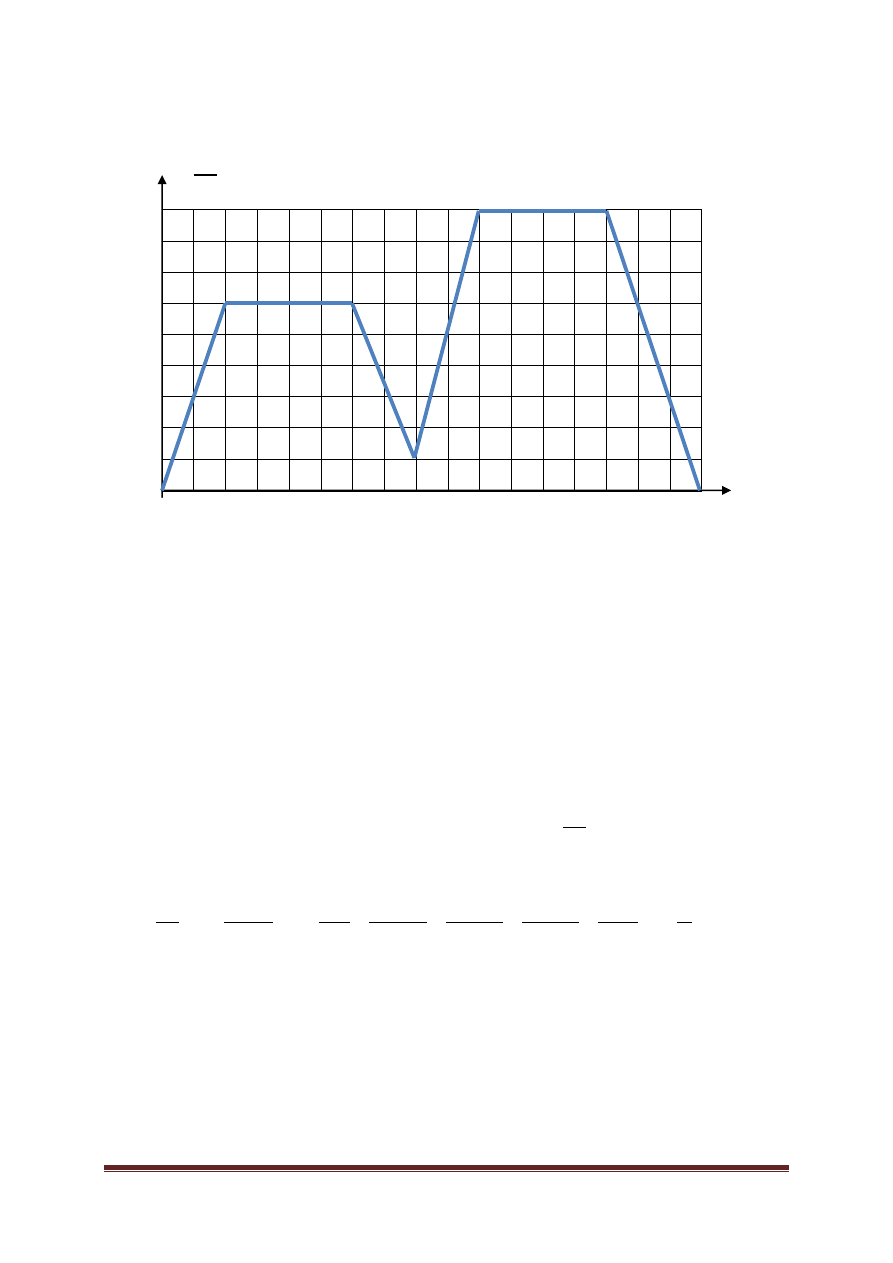
Zadanie 5. Przeanalizuj wykres ruchu pewnego ciała i udziel odpowiedzi na

poniżej przedstawione pytania.

𝒗

𝒌𝒎

𝒉

𝒕 𝒔

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

a) jakim ruchem poruszało się ciało na odcinkach:

AB –

ruch jednostajnie przyspieszony

BC –

ruch jednostajny

CD –

ruch jednostajnie opóźniony

DE –

ruch jednostajnie przyspieszony

EF –

ruch jednostajny

FG –

ruch jednostajnie opóźniony

b) Jaką maksymalną prędkość osiągnęło ciało? Podaj ją w m/s.

Odp. Ciało osiągnęło maksymalną prędkość równą

h

km

90

.

s

m

s

m

s

m

s

m

s

m

s

m

s

m

h

km

25

4

100

4

10

10

12

10

30

36

10

90

36

10

90

3600

1000

90

90

























90

80

70

60

50

50

40

30

20

10

A

B

C

D

E

G

F

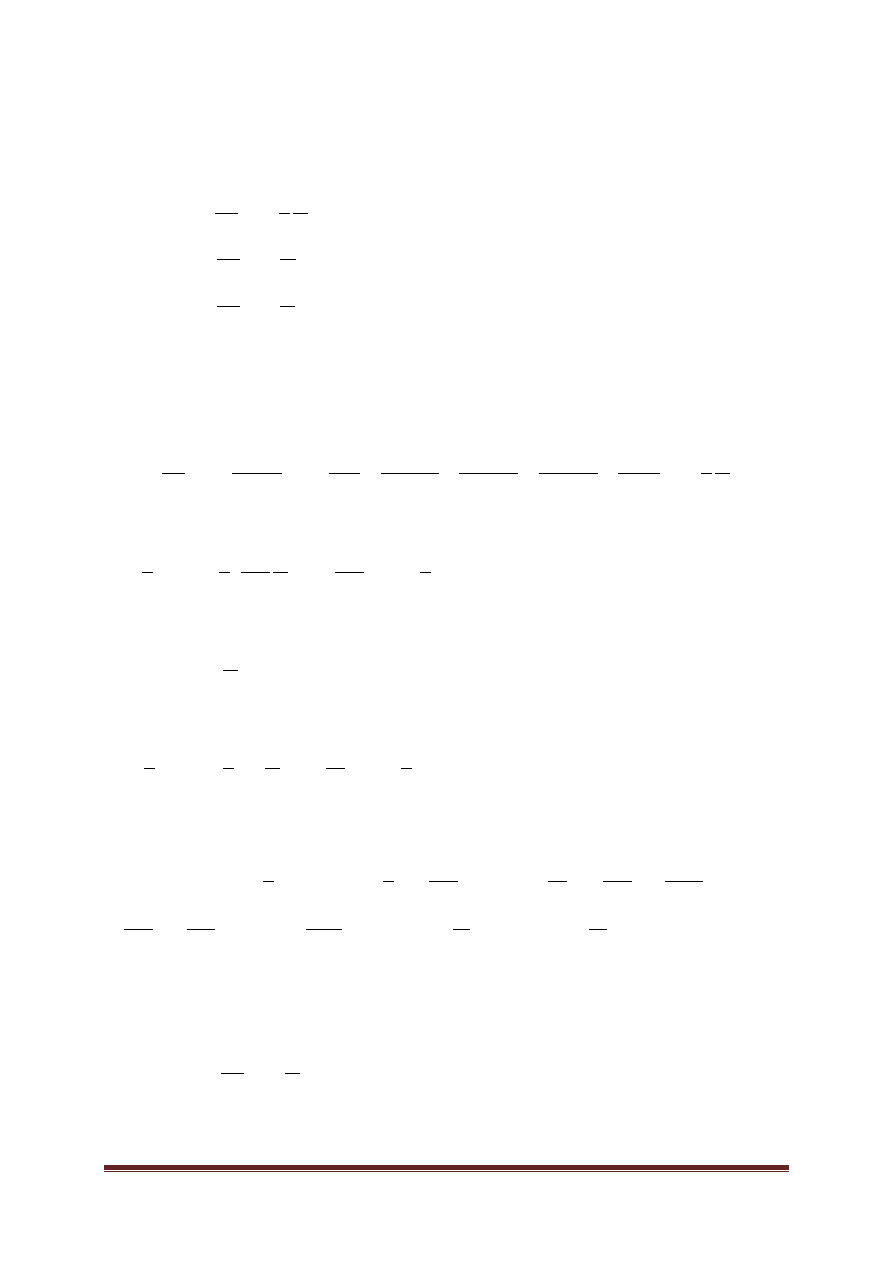
Ewa Mariola Lutkiewicz

Strona 6

c) Jaką drogę przebyło ciało do 8 sekundy ruchu?

Obliczamy drogę z trzech różnych ruchów:

Dane:

Szukane:

s

m

h

km

v

9

2

22

80

1





?

1



s

s

m

h

km

v

25

90

2





?

2



s

s

m

h

km

v

25

90

3





?

3



s

s

t

2

1



?



c

s

s

t

4

2



s

t

3

3



Zamieniamy jednostki prędkości:

s

m

s

m

s

m

s

m

s

m

s

m

s

m

h

km

v

9

2

22

9

200

9

10

20

18

10

40

36

10

80

36

10

80

3600

1000

80

80

1



























Na odcinku DE mamy do czynienia z ruchem jednostajnie przyspieszonym, więc obliczamy drogę ze wzoru:

m

m

s

s

m

t

v

s

9

2

22

9

200

2

9

200

2

1

2

1

1

1

1

















Na odcinku EF mamy do czynienia z ruchem jednostajnym prostoliniowym, więc obliczamy drogę ze wzoru:

m

s

s

m

t

v

s

100

4

25

2

2

2











Na odcinku FG mamy do czynienia z ruchem jednostajnie opóźnionym, więc obliczamy drogę ze wzoru:

m

m

s

s

m

t

v

s

2

1

37

2

75

3

25

2

1

2

1

3

3

3

















Dodajemy wszystkie obliczone wartości drogi:

m

m

m

m

m

m

m

m

m

m

m

m

m

m

m

m

m

s

s

s

s

c

18

13

159

100

18

13

59

100

18

1075

100

18

675

18

400

100

18

9

75

18

400

2

75

100

9

200

2

1

37

100

9

2

22

3

2

1













































d) Oblicz opóźnienie ruchu od 14 do 17 sekundy.

Dane:

Szukane:

s

m

h

km

v

25

90







?



a

s

t

3





Ewa Mariola Lutkiewicz

Strona 7

Na odcinku FG mamy do czynienia z ruchem jednostajnie opóźnionym, więc obliczamy przyspieszenie ze
wzoru:

2

2

3

1

8

3

25

3

25

s

m

s

m

s

s

m

t

v

a













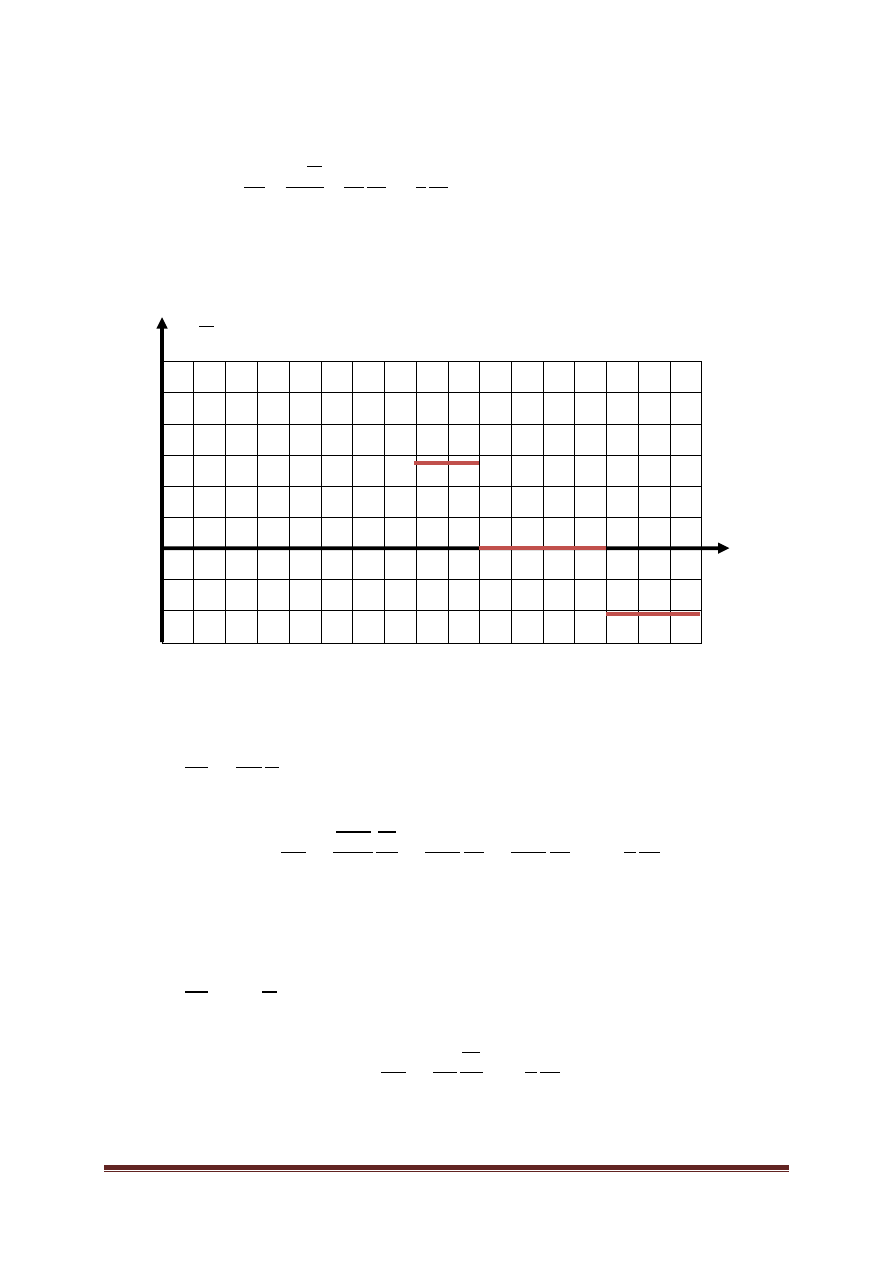
e) Narysuj wykres zależności przyspieszenia a od czasu t dla ruchu od 8 do

17 sekundy.

𝒂

𝒎

𝒔

𝟐

𝒕 𝒔

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Obliczamy z jakim przyspieszeniem porusza się ciało na odcinku DE:

Dane:

Szukane:

∆𝑣 = 80

𝑘𝑚

ℎ

=

200

9

𝑚

𝑠

𝑎

1

=?

∆𝑡 = 2𝑠

𝑎

1

=

∆𝑣

∆𝑡

=

200

9

2

𝑚

𝑠

𝑠

=

200

18

𝑚

𝑠

2

=

100

9

𝑚

𝑠

2

= 11

1
9

𝑚

𝑠

2

Na odcinku EF ciało porusza się ruchem jednostajnym prostoliniowym, więc nie posiada przyspieszenia.
Obliczamy z jakim opóźnieniem porusza się ciało na odcinku FG:

Dane:

Szukane:

∆𝑣 = 90

𝑘𝑚

ℎ

= 25

𝑚

𝑠

𝑎

2

=?

∆𝑡 = 3𝑠

𝑎

2

=

∆𝑣

∆𝑡

=

25

3

𝑚

𝑠

𝑠

= 8

1
3

𝑚

𝑠

2

Wszystkie obliczone wartości wstawiamy na wykresie.

24

20

16

12

50

8

4

0

-4

-8

D

E

F

G