K

i

n

e ma t

y

c z n

y

o

p

i

s

r u

c h

u

j

e d

n

o

w

y

mi

a r o

w

e g

o

$

#

g

u

i

d

{

0

8

1

F

C

0

9

8

-

7

E

C

0

-

4

4

9

5

-

A

E

5

9

-

B

4

A

B

4

4

E

7

A

2

4

5

}

#

$

M

e

c

h

an

i

k

a

–

c

z

ym

j

e

s t

?

M e

c

h

a

n

i

k

a

k

l

a

s

y

c

z

n

a

=

me

c

h

a

n

i

k

a

n

i

e

k

w

a

n

t

o

w

a

I

s t

n

i

e

j

ą

t

r

z

y

f

or

m

a

l

i

z

m

y

opi

s u m

e

c

ha

ni

k

i

kl

a

s yc

z

ne

j

:

-

f

or

m

a

l

i

z

m

N

e

w

t

ona

(

poj

ę

c

i

e

s

i

ł

y,

t

r

z

y pr

a

w

a

r

u

c

hu)

-

f

or

m

a

l

i

z

m

L

a

gr

a

ng

e

’

a

-

f

or

m

a

l

i

z

m

H

a

m

i

l

t

ona

M e

c

ha

n

i

k

a

t

o na

uka

o r

u

c

hu c

i

a

ł

(

j

a

k

por

us z

a

s

i

ę

pi

ł

ka

,

poc

i

s k, w

a

h

a

dł

o, p

l

a

ne

t

a

c

z

y kom

e

t

a

)

.

M e

c

h

a

n

i

k

a

k

l

a

s

y

c

z

n

a

o

b

e

j

m

u

j

e

:

k

i

n

e

ma

t

y

k

ę

(

f

o

r

m

a

l

n

y

o

p

i

s

r

u

c

h

u

,

n

i

e

m

a

s

i

ł

)

d

y

n

a

mi

k

ę

(

p

r

z

y

c

z

y

n

y

r

u

c

h

u

i

p

o

w

i

ą

z

a

n

i

e

r

u

c

h

u

z

w

ł

a

s

n

o

ś

c

i

a

m

i

c

z

ą

s

t

e

k

)

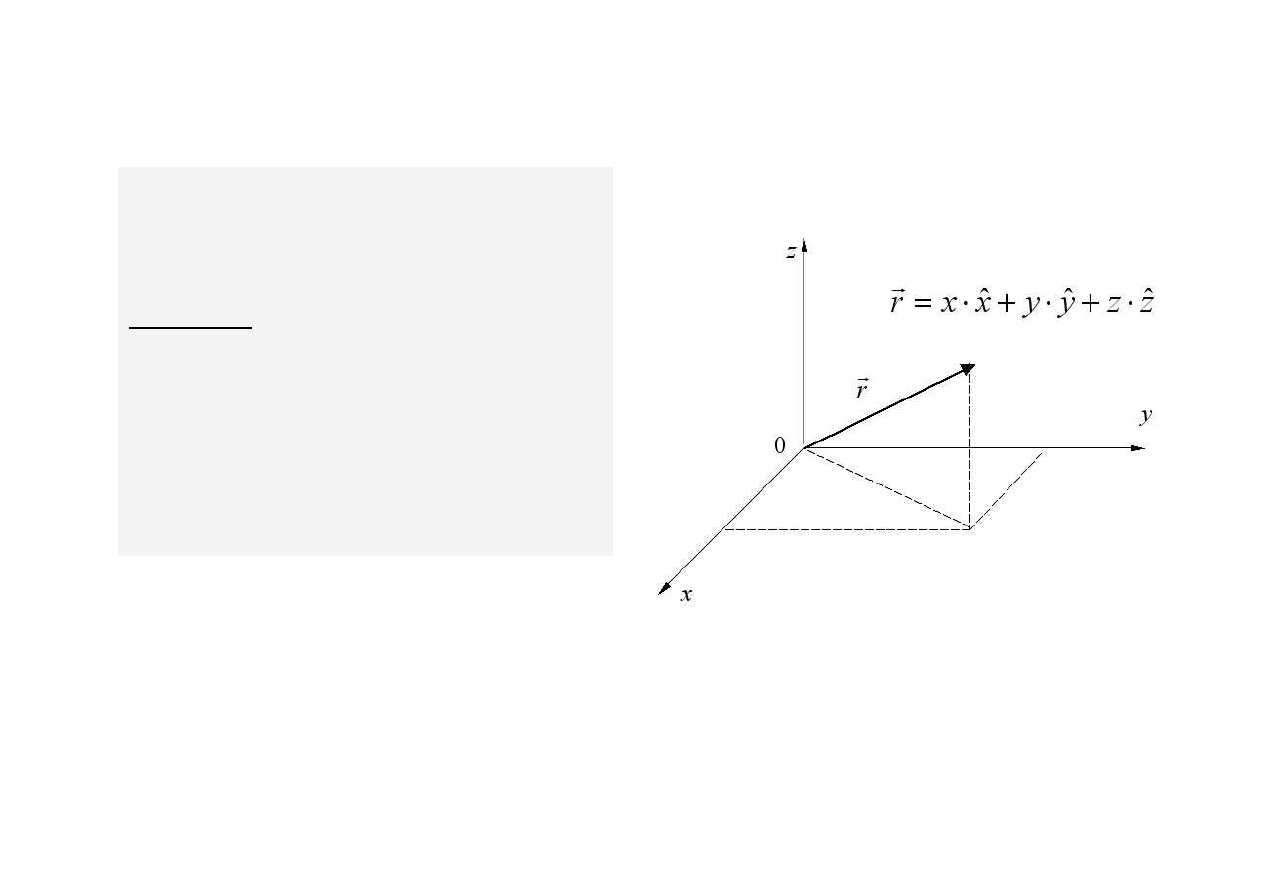
P

o

j

ę

c

i

e

i

o

p

i

s

r

u

c

h

u

R

u

c

h

–

z

m

i

a

n

a

p

o

ł

o

ż

e

n

i

a

p

o

ł

o

ż

e

n

i

a

c

i

a

ł

a

w

p

r

z

e

st

r

z

e

n

i

z

u

p

ł

y

w

e

m

c

z

a

su

w

z

g

l

ę

d

e

m

p

e

w

n

y

c

h

o

b

i

e

k

t

ó

w

m

a

t

e

r

i

a

l

n

y

c

h

t

w

o

r

z

ą

c

y

c

h

u

k

ł

a

d

o

d

n

i

e

si

e

n

i

a

(

U

O

)

,

k

t

ó

r

e

g

o

m

a

t

e

m

a

t

y

c

z

n

y

m

w

y

r

a

z

e

m

j

e

s

t

u

k

ł

a

d

w

sp

ó

ł

r

z

ę

d

n

y

c

h

(

U

W

)

.

N

a

j

c

z

ę

śc

i

e

j

st

o

so

w

a

n

y

j

e

st

k

a

r

t

e

z

j

a

ń

s

k

i

U

W

,

a

l

e

U

W

m

o

ż

e

b

y

ć

n

i

e

s

k

o

ń

c

z

e

n

i

e

w

i

e

l

e

.

C

z

ąs t

k

a k

l

a

s yc

z

n

a

t

r

a

k

t

ow

a

na

j

a

ko

punkt

m

a

t

e

r

i

a

l

ny

por

us z

a

s

i

ę

po okr

e

ś l

on

ym

t

or

z

e

.

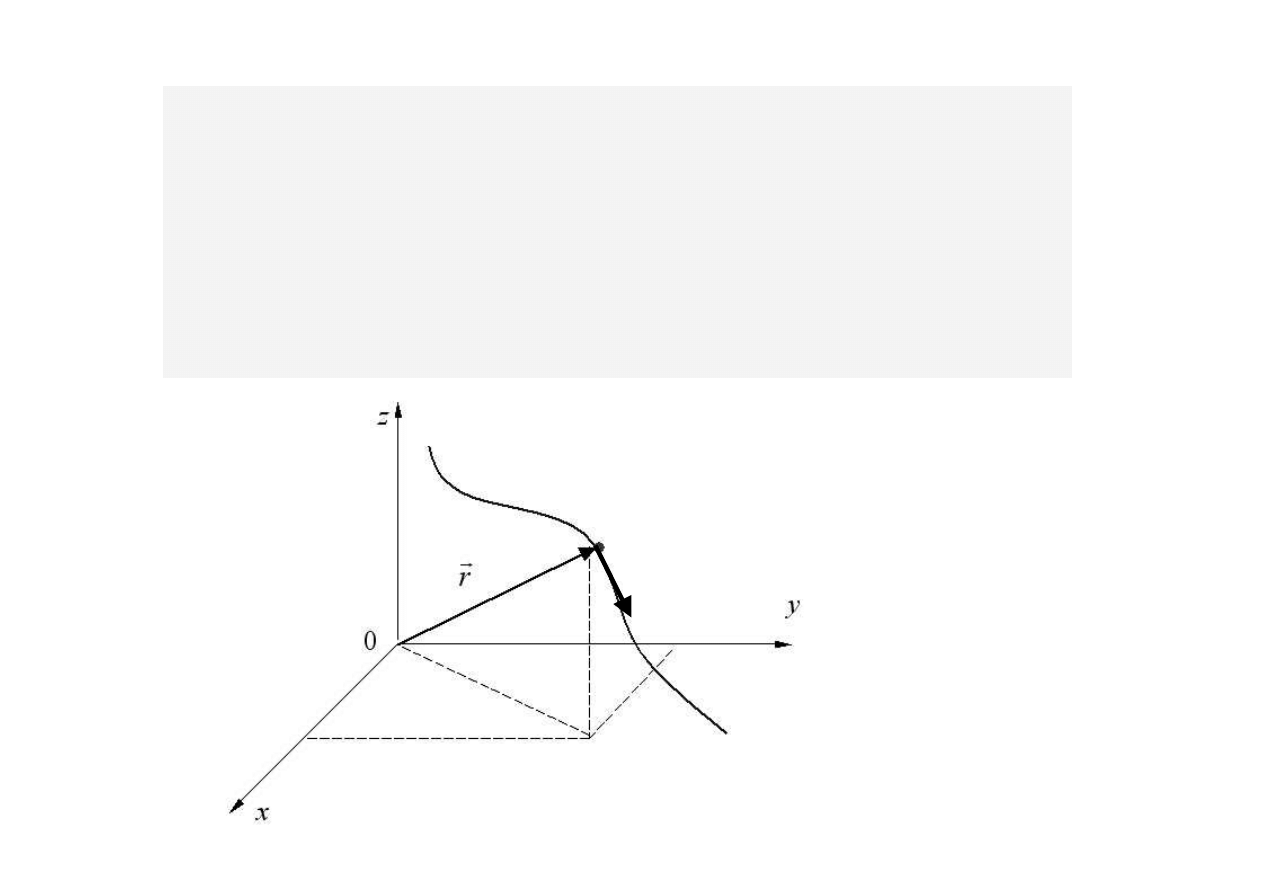
S

t

an

c

z

ąs t

k

i

k

l

as yc

z

n

e

j

j

e

s

t

w

pe

ł

n

i

okr

e

ś l

ony p

r

z

e

z

poda

ni

e

w

e

kt

or

a

poł

o

ż

e

n

i

a

r

i

w

e

k

t

or

a

pr

ę

dkoś

c

i

v w

da

ne

j

c

hw

i

l

i

. P

oni

e

w

a

ż

r

=

(

x,

y,z

)

or

a

z

v

=

(

v

x

, v

y

, v

z

)

oz

na

c

z

a

t

o

ogól

n

i

e

pod

a

ni

e

6

l

i

c

z

b.

v



K

i

n

e

ma

t

y

k

a

(

g

r

.

k

i

n

e

t

o

s

–

r

u

c

h

)

n

i

e

w

n

i

k

a

w

p

r

z

y

c

z

y

n

y

r

u

c

h

u

,

j

e

d

y

n

i

e

p

o

d

a

j

e

r

e

l

a

c

j

e

p

o

m

i ę

d

z

y

p

o

ł

o

ż

e

n

i

e

m

(

r

)

,

p

r

ę

d

k

o

ś

c

i

ą

(

v

)

i

p

r

z

y

s

p

i

e

s

z

e

n

i

e

m

(

a

)

.

D

oda

t

kow

o c

z

yn

i

s i

ę

z

a

ł

oż

e

n

i

e

o

j

e

d

nor

odnoś c

i

c

z

a

s u,

i

z

o

t

r

opow

oś c

i

p

r

z

e

s t

r

z

e

n

i

(

n

i

e

w

yr

óż

ni

a

s

i

ę

ż

a

dn

e

j

c

hw

i

l

i

c

z

a

s u, m

i

e

j

s

c

a

po

ł

oż

e

ni

a

, a

ni

k

i

e

r

unk

u)

or

a

z

z

a

ł

o

ż

e

n

i

e

,

ż

e

r

u

c

h

ni

e

z

m

i

e

n

i

a

w

ł

a

ś c

i

w

oś c

i

c

z

ą

s

t

k

i

P

r

z

yp

a

d

e

k

r

u

c

h

u

w

j

e

d

n

ym

w

ym

i

ar

z

e

(

1D

–

o

n

e

d

i

m

e

n

s i

o

n

)

O

pi

s ki

ne

m

a

t

yc

z

ny op

i

e

r

a

s i

ę

na

dw

óc

h de

f

i

n

i

c

j

a

c

h:

pr

ę

dkoś c

i

(

)

(

)

x

x

t

t

x

t

v

t

t

















pr

z

ys pi

e

s z

e

ni

a

(

)

(

)

v

v

t

t

v

t

a

t

t

















v

i

a

m

o

g

ą

b

y

ć

w

m

y

ś

l

d

e

f i n

i c

j i

z

a

r ó

w

n

o

d

o

d

a

t n

i e

j a

k

i

u

j e

m

n

e

( o

z

n

a

c

z

a

t o

j e

d

y

n

i e

,

ż

e

w

e

k

t o

r

j e

s

t

s

k

i e

r o

w

a

n

y

z

g

o

d

n

i e

l u

b

p

r z

e

c

i w

n

i e

d

o

z

w

r o

t u

o

s

i

x

) .

Ró

w

n

a

n

i a

( 1

a

)

i

( 1

b

)

t o

w

z

o

r y

r ó

ż

n

i c

o

w

e

( t a

k

l i c

z

y

k

o

m

p

u

t e

r

)

t j .

p

o

d

a

j ą

j a

k

z

m

i e

n

i ł a

s

i ę

w

a

r t o

ś

ć

x

i

v

w

c

z

a

s

i e

 t

(

c

z

y

l i

p

r z

e

d

s

t a

w

i a

j ą

w

a

r t o

ś

c

i

ś

r e

d

n

i e

w

c

z

a

s

i e

 t ) .

m

s













2

m

s













(

1

a

)

(

1

b

)

x

[

m

]

0

x

(

t

0

)

= x

0

v



1

W

X

V

I

I

w

. I

. N

e

w

t

on i

W

. L

e

i

bn

i

z

w

yna

l

e ź

l

i

r

a

c

hune

k

w

i

e

l

koś

c

i

n

i

e

s końc

z

e

n

i

e

m

a

ł

yc

h (

z

w

a

ny dz

i

ś

r

a

c

hunki

e

m

r

óż

n

i

c

z

kow

ym

i

c

a

ł

kow

ym

)

, c

o poz

w

ol

i

ł

o m

a

t

e

m

a

t

yc

z

n

i

e

z

de

f

i

n

i

ow

a

ć

pr

ę

dkoś ć

i

pr

z

ys pi

e

s z

e

ni

e

c

hw

i

l

ow

e

.

I

de

a

:

w

e

w

z

or

a

c

h

(

1a

)

i

(

1b)

pr

z

e

c

ho

dz

i

m

y do gr

a

ni

c

y



t



0

(

w

t

e

dy

t

a

k

ż

e



x



0

i



v



0, a

l

e

i

l

or

a

z

r

ó

ż

n

i

c

ow

y j

e

s t

r

ó

ż

ny

od z

e

r

a

i

m

a

ś c

i

s

ł

y s e

ns

m

a

t

e

m

a

t

yc

z

ny)

. M a

m

y

w

i

ę

c

pr

ę

dkoś ć

c

h

w

i

l

ow

a

:

0

(

)

l

i

m

t

x

d

x

v

t

x

t

d

t

















pr

z

ys pi

e

s z

e

ni

e

c

hw

i

l

ow

e

0

(

)

l

i

m

t

v

d

v

a

t

v

t

d

t

















P

r

ę

d

k

o

ś

ć

i

p

r

z

y

s

p

i

e

s

z

e

n

i

e

c

h

w

i

l

o

w

e

(

2a

)

(

2b)

W

m

a

t

e

m

a

t

yc

e

gr

a

n

i

c

ę

i

l

or

a

z

u r

ó

ż

n

i

c

ow

e

go na

z

yw

a

s i

ę

poc

hodną

f

unkc

j

i

.

O

z

na

c

z

e

ni

a

dx, dv i

d

t

m

oż

na

uw

a

ż

a

ć

j

a

ko gr

a

ni

c

e

:

d

x

=



x



0

,

d

v

=



v



0

,

d

t

=



t



0

;

S

ą

t

o

t

z

w

. r

ó

ż

ni

c

z

k

i

odp

ow

i

e

dni

o p

r

z

e

s un

i

ę

c

i

a

(

dx)

i

pr

ę

dko

ś c

i

(

dv)

.

W

z

or

y (

2a

)

i

(

2b)

t

o d

e

f

i

ni

c

j

e

i

n

i

e

z

a

w

i

e

r

a

j

ą

ż

a

dn

e

go pr

a

w

a

f

i

z

yc

z

ne

go,

c

z

yn

i

ą

j

e

dyn

i

e

p

e

w

ne

z

a

ł

oż

e

n

i

a

c

o do

c

z

a

s u

i

pr

z

e

s

t

r

z

e

n

i

ni

e

w

yr

óż

n

i

a

j

ą

c

ż

a

dn

e

j

c

hw

i

l

i

c

z

a

s u

i

po

ł

oż

e

ni

a

(

j

e

dnor

odno

ś ć

c

z

a

s u i

p

r

z

e

s

t

r

z

e

n

i

)

.

P

r

ę

d

k

o

ś

ć

i

p

r

z

y

s

p

i

e

s

z

e

n

i

e

j

a

k

o

p

o

c

h

o

d

n

e

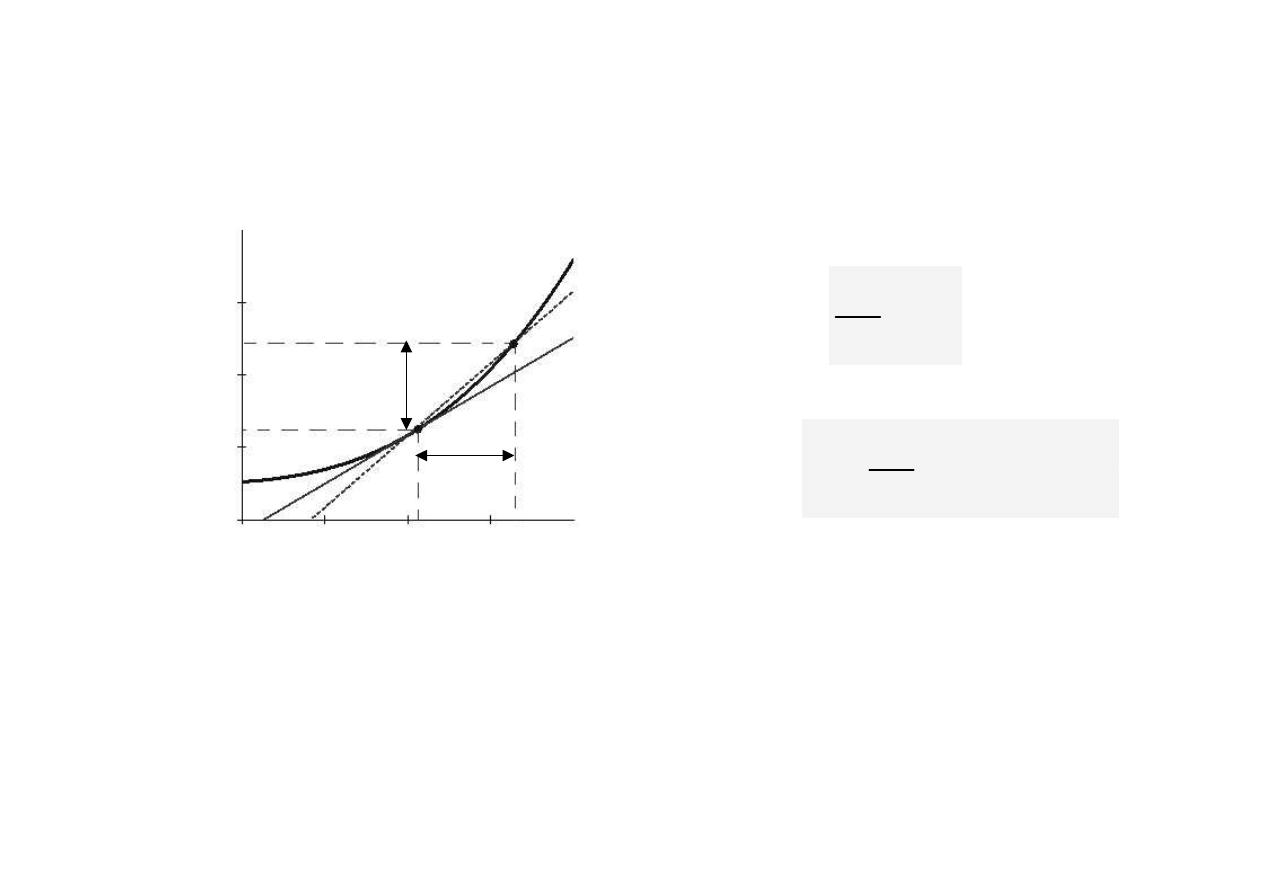
I

n

t

e

r

p

r

e

t

a

c

j

a

g

e

o

me

t

r

y

c

z

n

a

p

o

c

h

o

d

n

e

j

P

oc

hodna

w

da

nym

pun

kc

i

e

r

ów

na

j

e

s t

t

a

ng

e

ns o

w

i

na

c

hy

l

e

n

i

a

s t

yc

z

ne

j

do

kr

z

yw

e

j

w

t

ym

punkc

i

e

.

P

oc

hodna

poda

j

e

i

nf

or

m

a

c

j

ę

j

a

k s

z

ybko f

unkc

j

a

s i

ę

z

m

i

e

n

i

a

(

i

n

a

c

z

e

j

:

po

da

j

e

s t

op

i

e

ń

na

c

hy

l

e

n

i

a

f

unkc

j

i

w

da

nym

punkc

i

e

)

0

l

i

m

c

h w

i

l

t

x

t

g

v

t















W

y

kr

e

s

pr z

e

m

i

e

s

z

c

z

e

ni

a

x

od

c

z

a

s

u

t

n

a

c

h

y

l e

n

i e

s

i e

c

z

n

e

j :

n

a

c

h

y

l e

n

i e

s

t y

c

z

n

e

j :

s

r

x

v

t







t

t

+



t

x( t

)

c

z

a

s

x( t

+



t

)

x



t



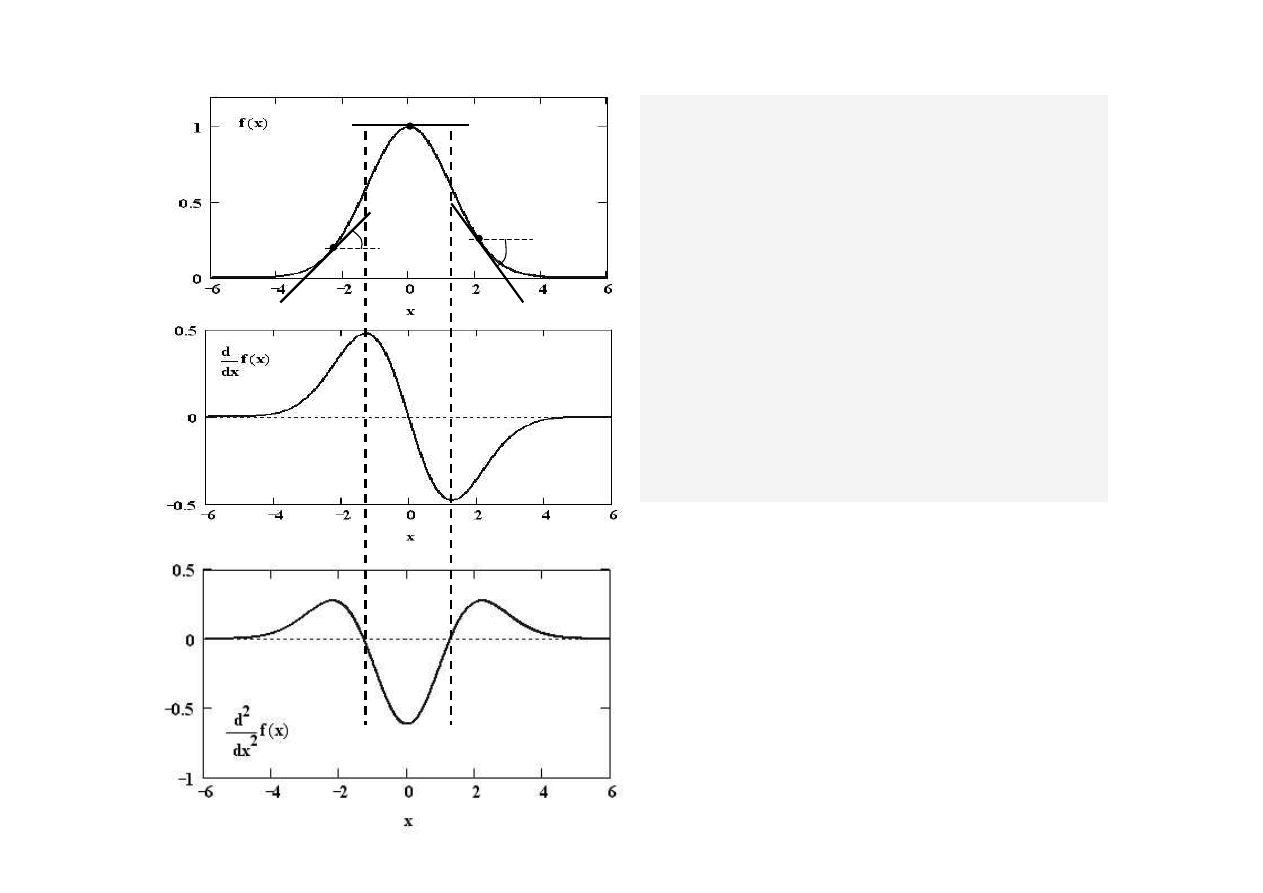
1

0

t

g





2

0

t

g





3

0

t

g





P o

c

h

o

d

n

a

p

o

d

a

j

e

„

st

r

o

m

o

ść

”

f

u

n

k

c

j

i

w

p

u

n

k

c

i

e

.

Li

c

z

b

o

w

o

r

ó

w

n

a

j

e

st

t

a

n

g

e

n

s

o

w

i

n

a

c

h

y

l

e

n

i

a

st

y

c

z

n

e

j

d

o

w

y

k

r

e

su

f

u

n

k

c

j

i

w

d

a

n

y

m

p

u

n

k

c

i

e

f

‘

=

t

g



.

F u

n

k

c

j

a

r

o

śn

i

e

:

p

o

c

h

o

d

n

a

>

0

F u

n

k

c

j

a

m

a

l

e

j

e

:

p

o

c

h

o

d

n

a

<

0

M

a

k

si

m

u

m

,

m

i

n

i

m

u

m

,

p

u

n

k

t

p

r

z

e

g

i

ę

c

i

a

:

p

o

c

h

o

d

n

a

=

0

.

Z

a

ł

ó

ż

m

y, ż

e

z

na

m

y z

a

l

e

ż

noś ć

a(

t

)

o

r

a

z

pr

ę

dkoś ć

poc

z

ą

t

kow

ą

v

(

t

0

)

i

po

ł

oż

e

ni

e

poc

z

ą

t

k

ow

e

x

(

t

0

)

.

J a

k w

yz

na

c

z

yć

z

m

i

a

ny w

c

z

a

s

i

e

pr

ę

d

koś c

i

v

(

t

)

i

p

oł

oż

e

n

i

a

x

(

t

)

, c

z

y

l

i

j

a

k m

ó

w

i

ą

m

a

t

e

m

a

t

y

c

y

:

j

a

k s c

a

ł

kow

a

ć

r

ów

na

ni

a

.

W

pr

os t

z

r

ó

w

na

ń

m

a

m

y

:

x(

t

0

+



t

)

=

x

(

t

0

)

+

v

(

t

0

)



t

v(

t

0

+



t

)

=

v

(

t

0

)

+

a

(

t

0

)



t

R

ów

na

ni

a

t

e

poka

z

u

j

ą

j

a

k z

na

l

e

ź

ć

w

i

e

l

koś

c

i

p

r

z

y

pr

z

e

s un

i

ę

c

i

u

o j

e

d

e

n kr

o

k c

z

a

s ow

y



t

.

N

u

m

e

r

yc

z

n

e

r

oz

w

i

ą

z

a

n

i

e

r

ów

n

ań

k

i

n

e

m

at

y

c

z

n

yc

h

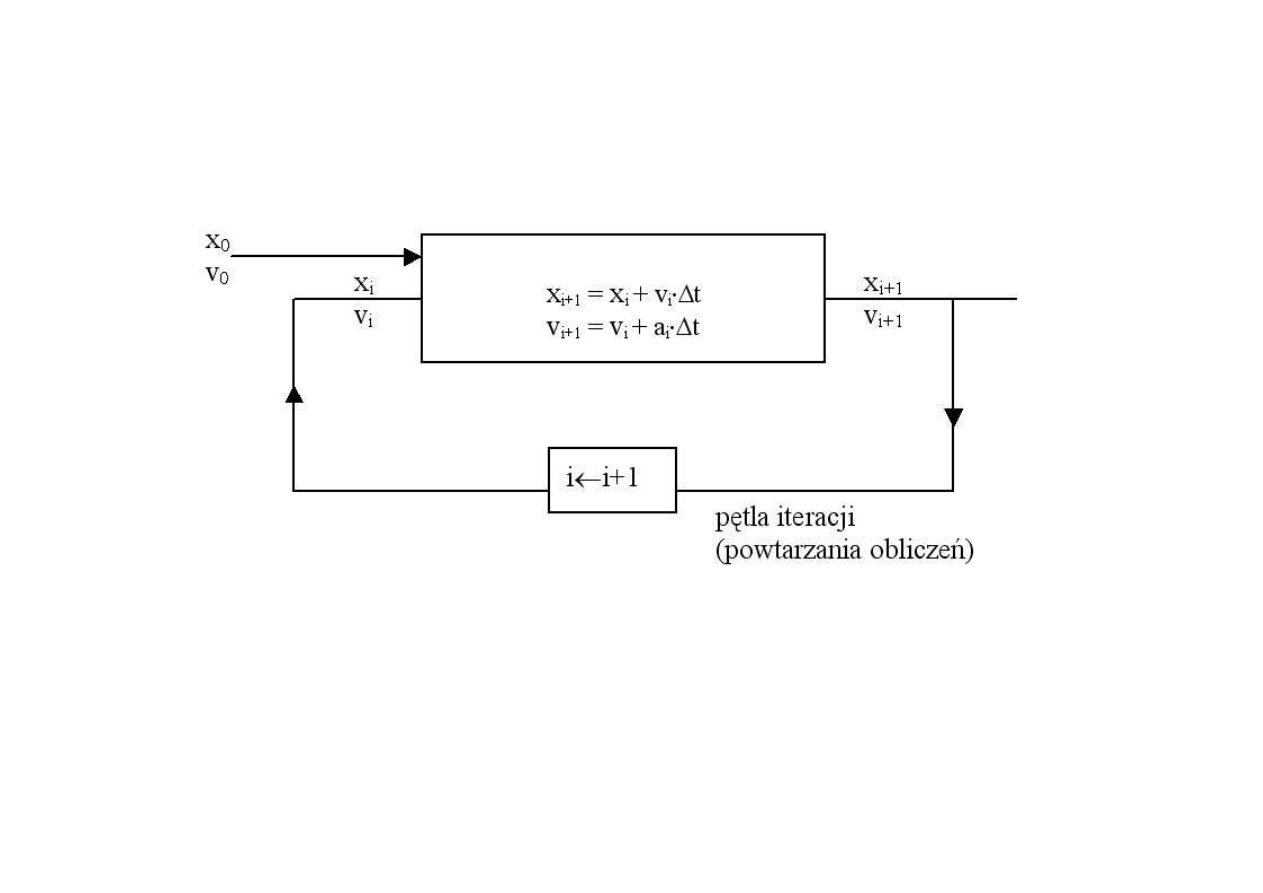
I m

p

l

e

m

e

n

t

ac

j

a n

a k

o

m

p

u

t

e

r

z

e .

J

e

ś l

i

i

nde

ks

i

=

0,1...N

num

e

r

uj

e

ko

l

e

j

n

e

kr

ok

i

c

z

a

s ow

e

, t

o

P

r

ogr

a

m

w

y

konuj

e

ko

l

e

j

ne

i

t

e

r

a

c

j

e

t

z

n. na

pods t

a

w

i

e

w

a

r

t

oś

c

i

x

i

, v

i

obl

i

c

z

a

x

i +1

v

i +1

. A

by z

a

c

z

ą

ć

ob

l

i

c

z

e

ni

a

n

a

l

e

ż

y w

pr

ow

a

dz

i

ć

„

z

z

e

w

ną

t

r

z

”

w

a

r

t

oś c

i

poc

z

ą

t

kow

e

x

0

i

v

0

(

t

j

. d

l

a

t

=

0 , c

z

y

l

i

i

=

0)

.

U

w

a

ga

:

x

i

o

z

na

c

z

a

po

ł

o

ż

e

n

i

e

(

w

s pół

r

z

ę

dn

ą

)

n

a

o

s i

x w

kr

oku i

-

t

ym

,

a

ni

e

pr

z

e

by

t

ą

d

r

ogę

t

j

. l

i

c

z

bę

pokon

a

nyc

h m

e

t

r

ó

w

)

.

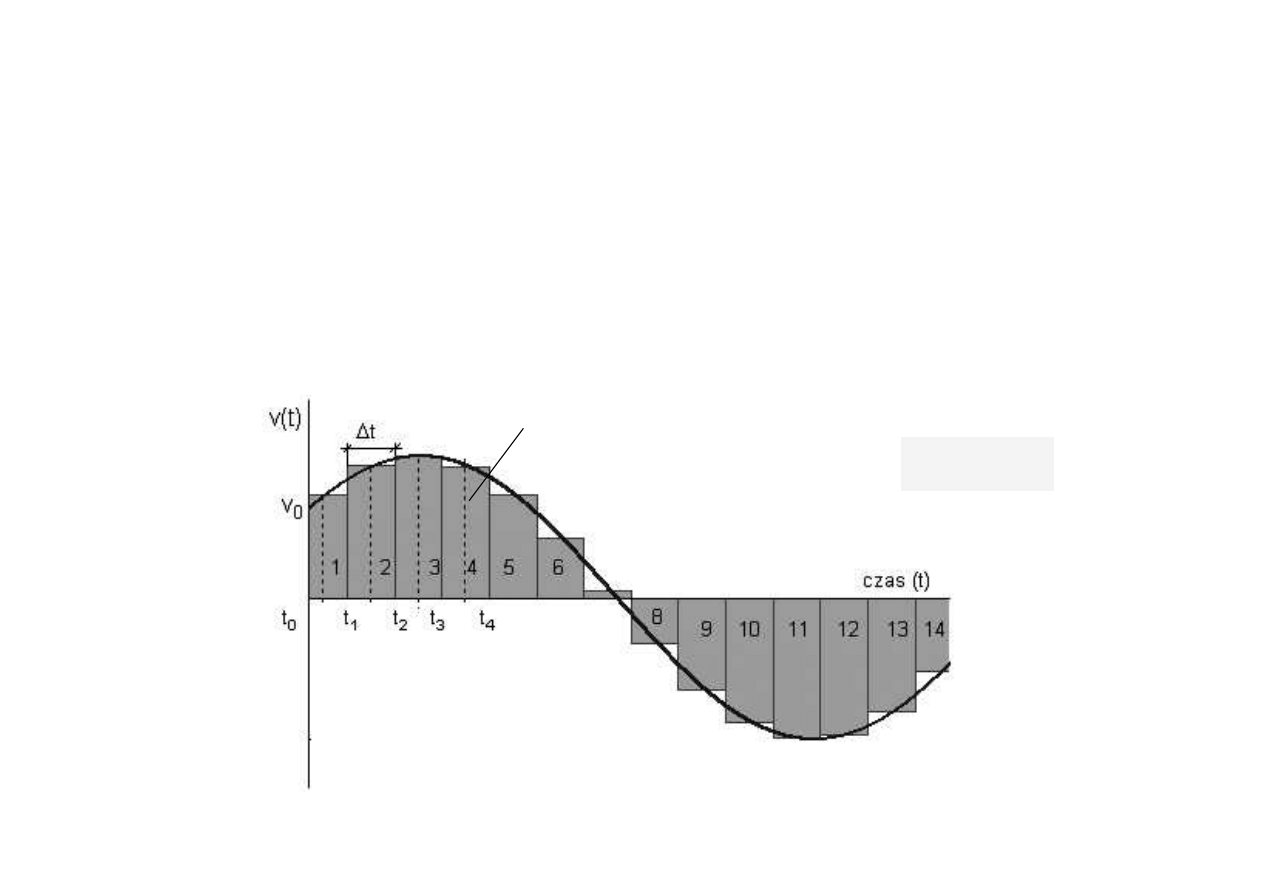
D

r

oga

j

ak

o

c

ał

k

a –r

oz

w

i

ą

z

an

i

e

an

al

i

t

yc

z

n

e

Cz

y

m

o

ż

n

a

w

y

p

r o

w

a

d

z

i ć

w

z

ó

r

m

a

t

e

m

a

t y

c

z

n

y

( z

a

l e

ż

n

o

ś

ć

a

n

a

l i t y

c

z

n

ą

)

z

g

o

d

n

i e

z

k

t

ó

r y

m

m

o

ż

n

a

o

b

l i c

z

y

ć

x

(

t )

z

n

a

j ą

c

v

(

t

)

i

o

b

l i c

z

y

ć

v

(

t )

z

n

a

j ą

c

a

(

t ) ?

M

o

ż

n

a

.

A

b

y

t

o

p

o

k

a

z

a

ć

z

a

ł

ó

ż

m

y

,

ż

e

z

n

a

m

y

z

a

l e

ż

n

o

ś

ć

p

r ę

d

k

o

ś

c

i

o

d

c

z

a

s

u

v

(

t )

( r y

s

)

i

c

h

c

e

m

y

z

n

a

l e

ź

ć

p

o

ł o

ż

e

n

i e

x

(

t ) .



x

i

=

v

i





t

=

pol

e

pr os

t

oką

t

a

x(

t

)

=

?

D

l

a

kr

z

yw

e

j

s c

hodkow

e

j

:

w

kr

oku 1

(

o dł

ugoś c

i



t

)

c

i

a

ł

o pr

z

e

byw

a

dr

ogę



x

1

=

v

1



t

, w

kr

ok

u 2

–

dr

ogę



x

2

=

v

2



t

,

w

kr

oku 3

–

dr

ogę



x

3

=

v

3



t

,

i

t

d. E

l

e

m

e

n

t

ar

n

a d

r

oga



x r

ów

n

a j

e

s t

p

ol

u

p

r

os t

ok

ąt

a

o p

od

s t

a

w

i

e



t

i

w

ys ok

oś c

i

v

i

.

K

r

oki

8-

14

da

j

ą



x <

0 ,

poni

e

w

a

ż

v

<

0 (

c

i

a

ł

o p

r

z

e

s uw

a

s i

ę

w

l

e

w

o)

.

K

ońc

ow

e

po

ł

oż

e

n

i

e

c

i

a

ł

a

na

os i

x, po

s ł

uguj

ą

c

s

i

ę

kr

z

yw

ą

s c

ho

dkow

ą

bę

dz

i

e

r

ów

ne

:

0

1

2

0

0

1

1

(

)

.

.

.

N

N

N

N

i

i

i

i

x

t

x

x

x

x

x

x

x

v

t





































A

p

r

o

k

s

y

m

a

c

j

a

k

r

z

y

w

e

j

g

ł

a

d

k

i

e

j

k

r

z

y

w

ą

s

c

h

o

d

k

o

w

ą

T

u

t a

j

N

=

1

4

.

P

o

n

i e

w

a

ż

p

o

s

ł u

g

u

j e

m

y

s

i ę

k

r z

y

w

ą

s

c

h

o

d

k

o

w

ą

w

y

n

i k

j e

s

t

p

r z

y

b

l i ż

o

n

y

.

A

b

y

z

b

l i ż

y

ć

s

i ę

d

o

z

a

d

a

n

e

j

k

r z

y

w

e

j

g

ł a

d

k

i e

j

v

( t )

n

a

l e

ż

y

b

r a

ć

c

o

r a

z

w

ę

ż

s

z

e

p

r o

s

t o

k

ą

t

y

,

a

ś

c

i ś

l e

p

r z

e

j ś

ć

d

o

g

r a

n

i c

y

 t



0

( w

t e

d

y

N





,

i

t

N

=

t

k

o

n

c

) :

0

0

0

0

1

(

)

l

i

m

(

)

(

)

k

o

n

c

t

N

k

o

n

c

i

t

i

t

N

x

t

x

v

t

t

x

v

t

d

t

























G

r a

n

i c

z

n

ą

s

u

m

ę

o

z

n

a

c

z

a

s

i ę

z

n

a

k

i e

m



;

j e

s

t

t o

z

n

i e

k

s

z

t a

ł c

o

n

a

l i t e

r

a

S

( ł a

c

.

s

u

m

m

a

)

i

n

o

s

i

n

a

z

w

ę

c

a

ł k

i

o

z

n

a

c

z

o

n

e

j

w

g

r a

n

i c

a

c

h

o

d

t

0

d

o

t

k

o

n

c

C

a

ł k

a

r

ó

w

n

a

j e

s

t

p

o

l u

p

o

w

i e

r

z

c

h

n

i

p

o

d

k

r

z

y

w

ą

v

(

t

)

j a

k

o

s

u

m

a

n

i e

s

k

o

ń

c

z

e

n

i

e

w

i e

l u

p

ó

l

p

r o

s

t o

k

ą

t ó

w

v

(

t ) d

t

( d

l a

v

( t )

<

0

p

o

l e

b

i e

r z

e

m

y

j a

k

o

u

j e

m

n

e

,

n

p

.

z

g

o

d

n

i e

z

z

a

m

i e

s

z

c

z

o

n

y

m

r y

s

u

n

k

i e

m

c

a

ł k

o

w

i t e

p

r z

e

m

i e

s

z

c

z

e

n

i e

 x

=

x

k

o

n

c



x

0

=

0

,

p

o

n

i e

w

a

ż

c

i a

ł o

p

o

r u

s

z

a

s

i ę

n

a

j p

i e

r w

w

p

r a

w

o

( v

>

0

)

a

p

o

t e

m

t y

l e

s

a

m

o

m

e

t

r

ó

w

w

l e

w

o

( v

<

0

) .

G

r

a

n

i

c

a

s

u

my

=

c

a

ł

k

a

o

z

n

a

c

z

o

n

a

Z

upe

ł

n

i

e

a

n

a

l

og

i

c

z

n

i

e

m

oż

na

poka

z

a

ć

,

ż

e

0

0

(

)

(

)

k

o

n

c

t

k

o

n

c

t

v

t

v

a

t

d

t







gdz

i

e

c

a

ł

k

a

r

ów

na

j

e

s

t

po

l

u pow

i

e

r

z

c

hni

pod kr

z

y

w

ą

pr

z

ys pi

e

s z

e

ni

a

a

(

t

)

.

R

e

gu

ł

a

x

(

t

ko

n

c

)



x

(

t

0

)

=

pol

e

pow

i

e

r

z

c

hn

i

p

od

v

(

t

)

v

(

t

ko

n

c

)



v

(

t

0

)

=

pol

e

pow

i

e

r

z

c

hni

pod

kr

z

yw

ą

a(

t

)

s ą

r

e

gu

ł

a

m

i

ś c

i

s

ł

ym

i

. Z

a

w

s z

e

t

a

k m

oż

na

l

i

c

z

y

ć

.

P

r

ę

d

k

o

ś

ć

j

a

k

o

c

a

ł

k

a

z

p

r

z

y

s

p

i

e

s

z

e

n

i

a

W

ykr

e

s z

m

i

a

n poł

o

ż

e

n

i

a

punkt

u na

o

s i

x

d

l

a

z

a

d

a

ne

j

f

unkc

j

i

pr

ę

dkoś c

i

v

(

t

)

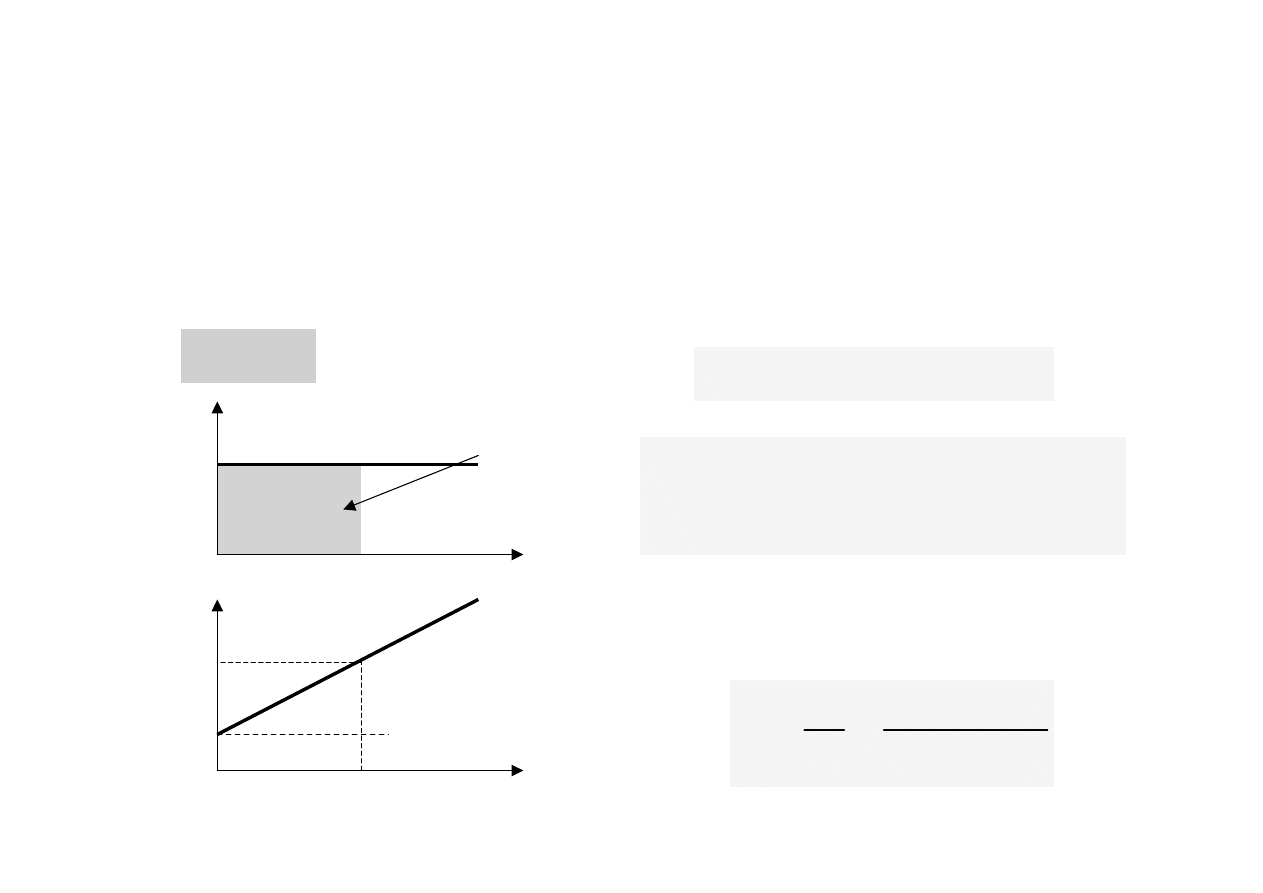
R

u

c

h

d

l

a a

= c

on

s t

an

s

D

l

a

pr

z

yp

a

d

ku

a

=

c

ons

t

a

ns

ł

a

t

w

o uz

ys ka

ć

w

z

or

y

a

na

l

i

t

y

c

z

n

e

dl

a

v

(

t

)

i

x

(

t

)

,

po

ni

e

w

a

ż

c

a

ł

k

ow

a

ni

e

s pr

o

w

a

dz

a

s i

ę

d

o obl

i

c

z

a

n

i

a

pol

a

pr

os t

yc

h f

i

g

ur

ge

om

e

t

r

y

c

z

nyc

h.

a

=

0

d

r

o

g

a

=

v

0

(

t

-

t

0

)

=

p

o

l

e

p

ro

st

o

k

ą

t

a

t

0

t

v

0





0

0

0

0

0

0

(

)

t

t

x

t

x

v

d

t

x

v

t

t













v

(

t

)

=

v

0

=

c

ons t

a

ns

l

u

b

z

f

a

k

t

u

,

ż

e

p

r

.

c

h

w

i

l

o

w

a

=

p

r

.

ś

r

e

d

n

i

a

0

0

0

(

)

(

)

x

t

x

t

d

x

v

d

t

t

t









x

(

t

)

t

x

0

t

0

v

0

(

t

-

t

0

)







a

=

c

ons

t

a

ns



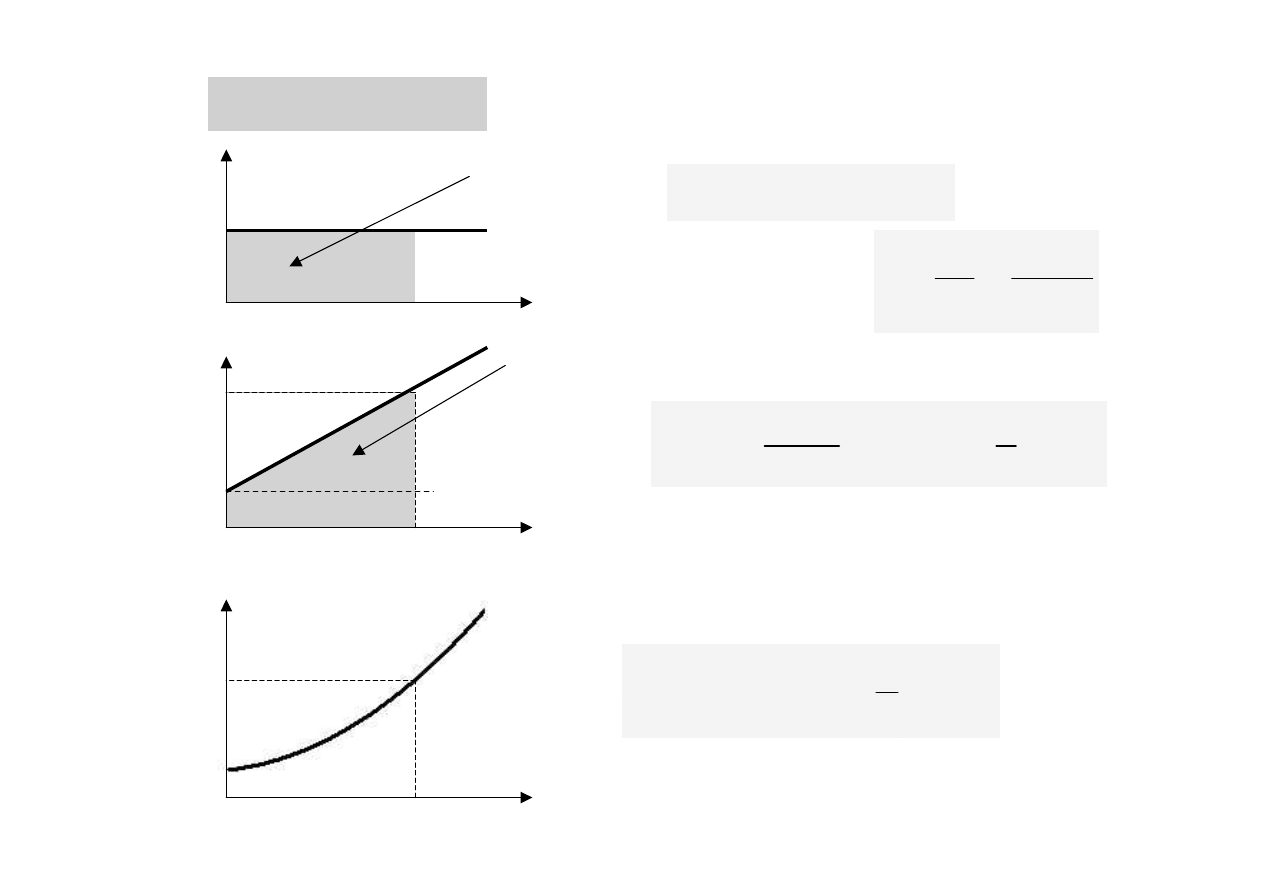
0

t

0

t

x

(

t

)

x

0

t

0

t

a

pol

e

=

z

m

i

a

na

pr ę

dkoś

c

i

0

0

(

)

(

)

v

t

v

a

t

t







l

u

b

z

f

a

k

t

u

,

ż

e

a

c hwilowe

=

a

śr e dnie

0

0

v

v

d v

a

d t

t

t









v

(

t

)

t

v

0

t

0

a(

t

-

t

0

)







pol

e

=

z

m

i

a

na

poł

oż

e

ni

a

0

0

0

1

2

2

v

v

x

x

t

v

t

a

t

t



















pol

e

t

r a

pe

z

u

pol

e

pr os

t

ok

ą

t

a

+

pol

e

t

r ój

ką

t

a

2

0

0

1

(

)

(

)

2

x

t

x

v

t

a

t











r ów

na

ni

e

p

a

r a

bo

l

i

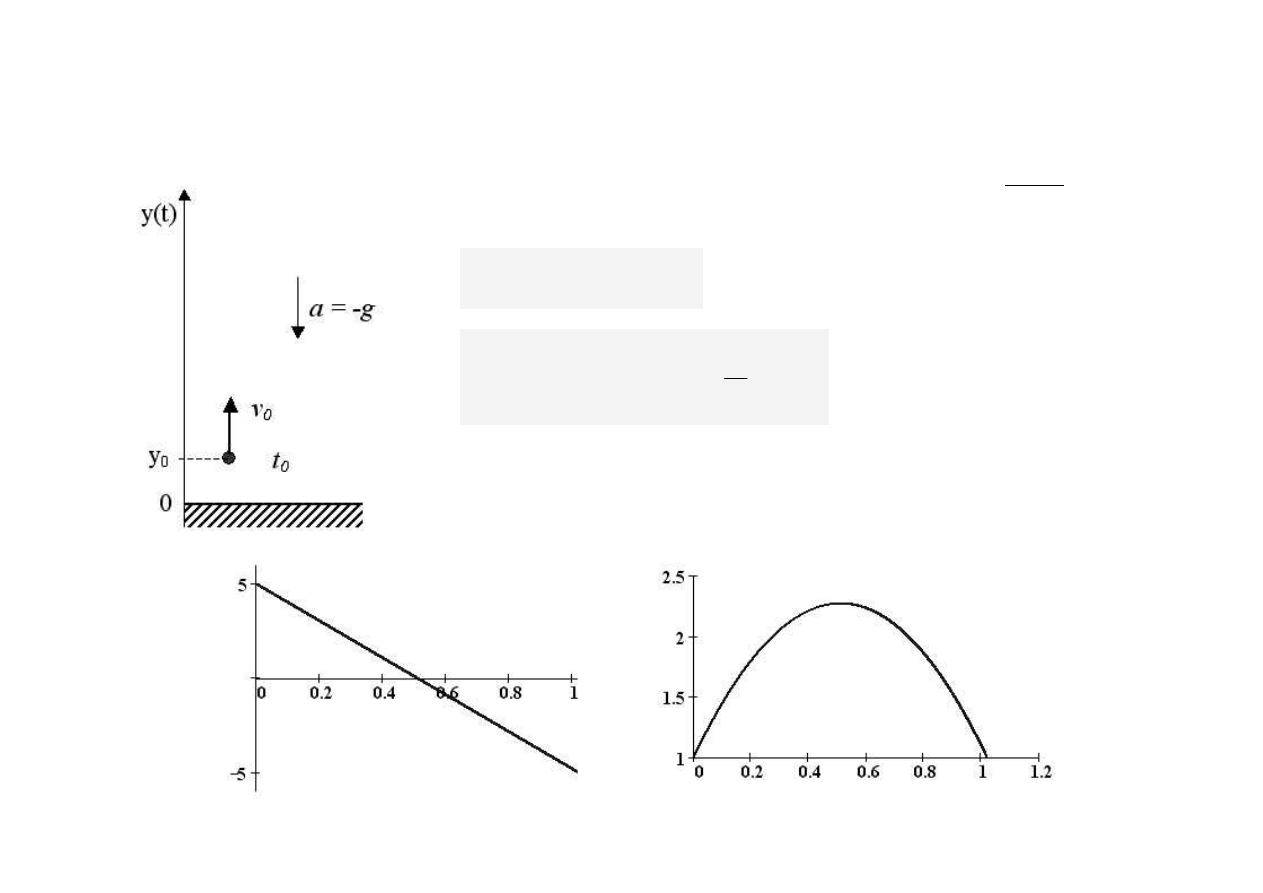
R

z

u

t

p

i

on

o

w

y

0

(

)

v

t

v

g

t







2

0

0

1

(

)

2

y

t

y

v

t

g

t











W

z

or

y na

pr

ę

dkoś ć

i

poł

oż

e

n

i

e

op

i

s u

j

ą

c

a

ł

y

r

uc

h (

w

z

nos

z

e

n

i

e

i

opa

d

a

ni

e

)

Z

a

ł ó

ż

m

y

:

t

0

=

0

,

v

0

=

5

m

/ s

,

g

=

9

,

8

1

m

/ s

2

.

t

[ s

]

t

[ s

]

v[ m

/

s

]

x[ m

]

D ZI ĘKU

J

Ę