G

e

o

m

e

tr

ia

e

li

p

s

o

id

y

G

e

o

m

e

tr

ia

e

li

p

s

o

id

y

J

a

n

u

s

z

W

a

lo

J

a

n

u

s

z

W

a

lo

J

a

n

u

s

z

W

a

lo

v

e

r

v

e

r

v

e

r

.

1.

1

(

1

0.

2

0

0

8)

.

1.

1

(

1

0.

2

0

0

8)

.

1.

1

(

1

0.

2

0

0

8)

(C

)

jw

(C

)

jw

2

2

/

3

2

/

3

2

E

li

p

s

o

id

a

o

b

ro

to

w

a

E

li

p

s

o

id

a

o

b

ro

to

w

a

(1

)

(1

)

d

n

o

o

ce

a

n

ó

w

el

ip

so

id

a

p

o

w

ie

rz

ch

n

ie

p

o

zi

o

m

e

p

o

zi

om

m

o

rz

a

N

H

P

lin

ia

pio

nu

g

eo

id

a

el

ip

so

id

a

po

w

ie

rz

ch

n

ia

l

ąd

ów

(C

)

jw

(C

)

jw

3

3

/

3

2

/

3

2

E

li

p

s

o

id

a

o

b

ro

to

w

a

E

li

p

s

o

id

a

o

b

ro

to

w

a

(2

)

(2

)

a

b

ω

a

b

a

f

−

=

2

2

2

2

a

b

a

e

−

=

2

2

2

2

b

b

a

e

−

=

′

f

=

2

9

8

.2

5

7

f

=

2

9

8

.2

5

7

-

-

1

1

±

±

5

5

×

×

1

0

1

0

-

-

6

6

a

=

6

3

7

8

1

3

7

m

a

=

6

3

7

8

1

3

7

m

±

±

3

m

3

m

(C

)

jw

(C

)

jw

4

4

/

3

2

/

3

2

E

li

p

s

o

id

a

o

b

ro

to

w

a

E

li

p

s

o

id

a

o

b

ro

to

w

a

(3

)

(3

)

2

1

1

1

e

a

b

f

−

−
=
−
=

e

e

e

2

2

2

1

=

′

+

′

2

2

2

1

'

e

e

e

−

=

b

a

e

=

−

1

2

,

1

2

e

b

a

−

=

(

)

(

)

1

1

1

2

2

−

+

′

=

e

e

f

e

f

f

e

2

,

2

2

2

2

≈

−

=

(C

)

jw

(C

)

jw

5

5

/

3

2

/

3

2

E

li

p

s

o

id

a

o

b

ro

to

w

a

E

li

p

s

o

id

a

o

b

ro

to

w

a

(4

)

(4

)

1

2

2

2

2

2

=
+

+

b

z

a

y

x

τ

=

=

+

′

a

b

e

2

2

2

1

2

1

1

e

a

lb

o

−
=

−

τ

2

2

2

2

a

z

y

x

=

+
+

τ

(C

)

jw

(C

)

jw

6

6

/

3

2

/

3

2

W

s

p

W

s

p

ó

ó

ł

ł

rz

rz

ę

ę

d

n

d

g

d

o

d

d

z

y

jn

d

d

n

d

g

d

o

d

d

z

y

jn

d

ω

x

y

z

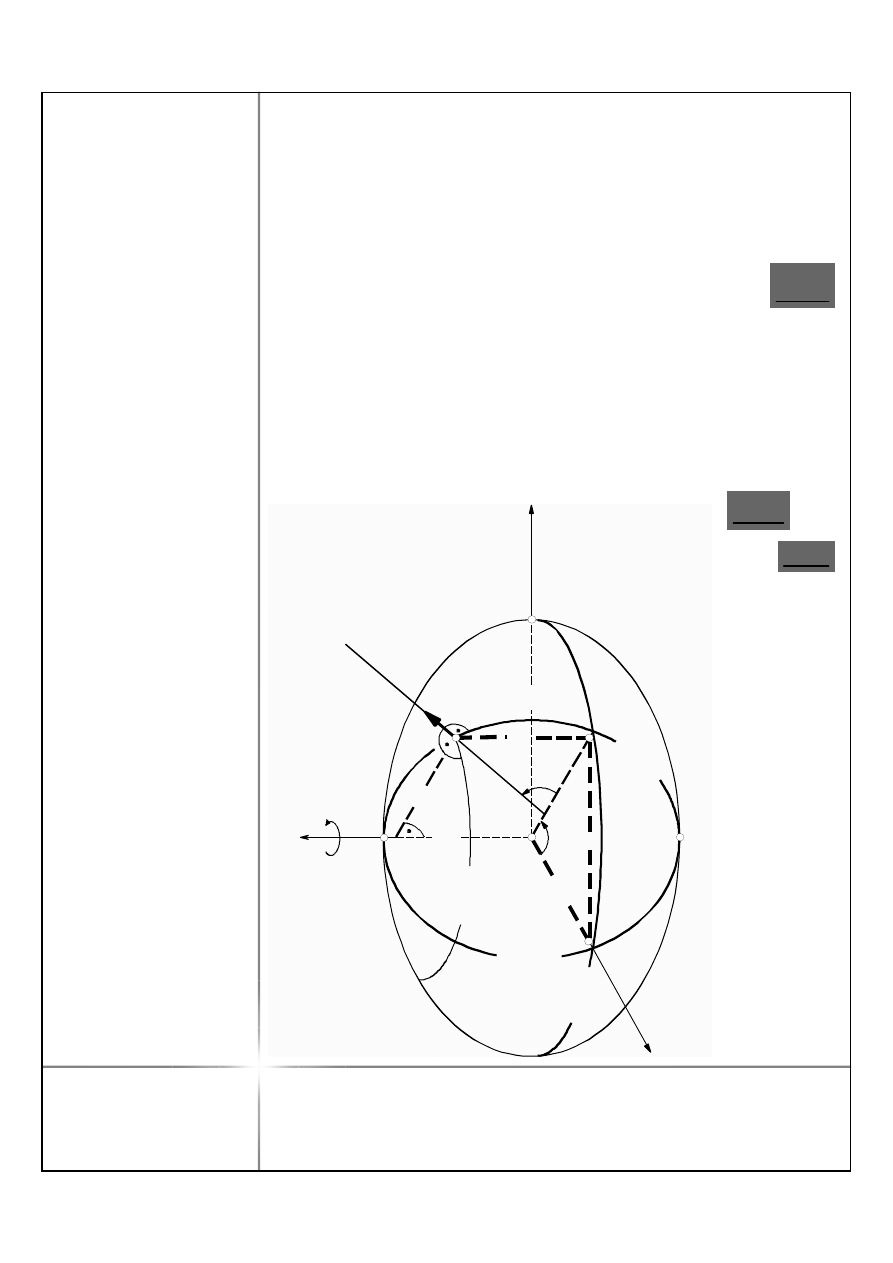
N

p

S

x

y

P

a

b

O

z

B

=

B

p

L

=

L

p

B

=

B

o

L =

L

o

n

B

p

L

p

no

rm

al

na

el

ip

so

id

y

w

p

un

kc

ie

P

S

z

e

ro

k

o

ś

ć

g

e

o

d

e

z

y

jn

a

B

(0

o

÷±

9

0

o

)

N

S

D

łu

g

o

ś

ć

g

e

o

d

e

z

y

jn

a

L

(0

0

÷3

6

0

o

)

lu

b

(

0

o

÷±

1

8

0

o

)

E

E

W

(C

)

jw

(C

)

jw

7

7

/

3

2

/

3

2

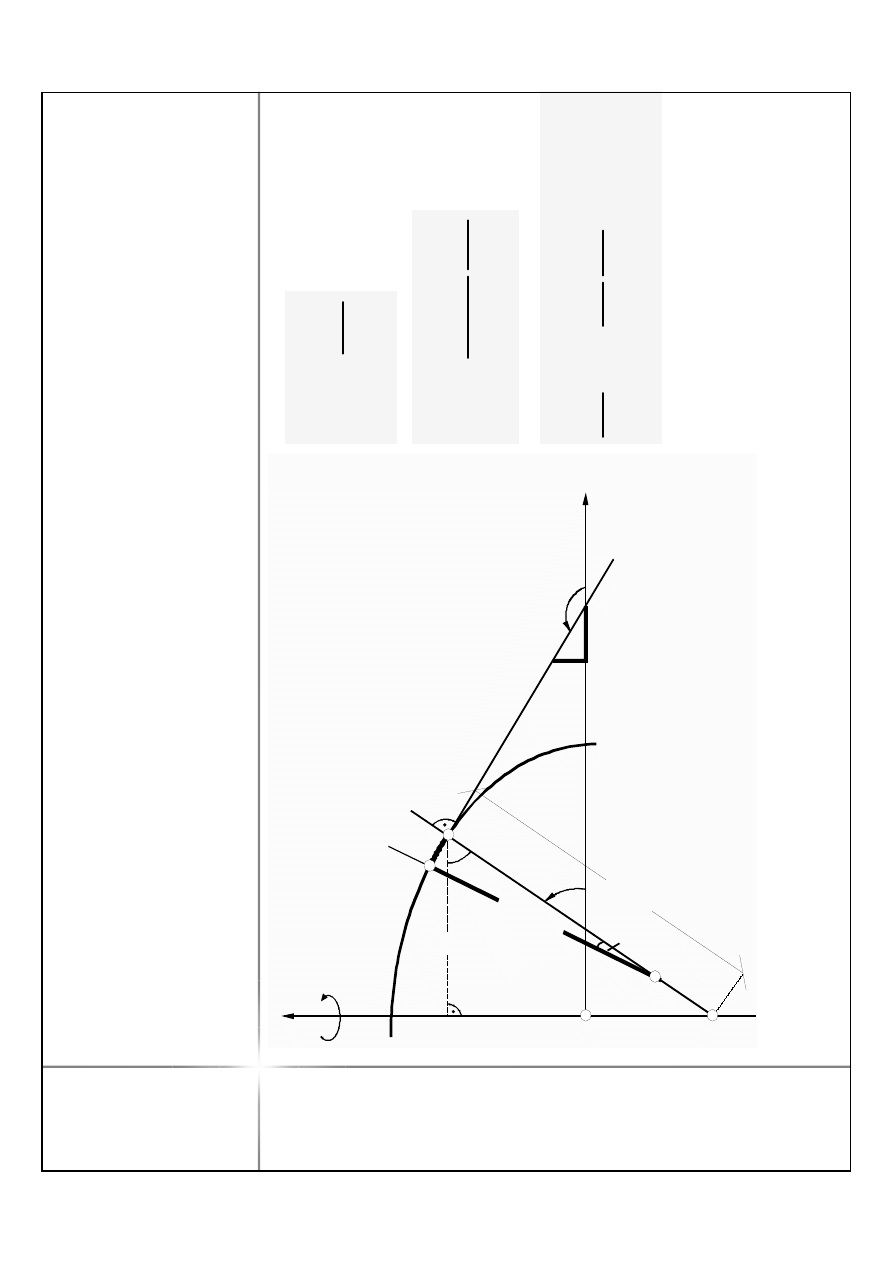
P

ro

m

id

P

ro

m

id

ń

ń

k

rz

y

w

iz

n

y

p

o

k

rz

y

w

iz

n

y

p

o

ł

ł

u

d

n

ik

a

u

d

n

ik

a

(1

)

(1

)

B

+

9

0

o

d

p

d

z

T

x/

y

P

B

d

s

P

'

p

B

d

B

O

O

p

M

N

ω

z

d

B

d

s

M

=

d

B

d

p

B

M

si

n

1

=

co

tB

a

p

z

b

d

p

d

z

−

=

−

=

2

2

(C

)

jw

(C

)

jw

8

8

/

3

2

/

3

2

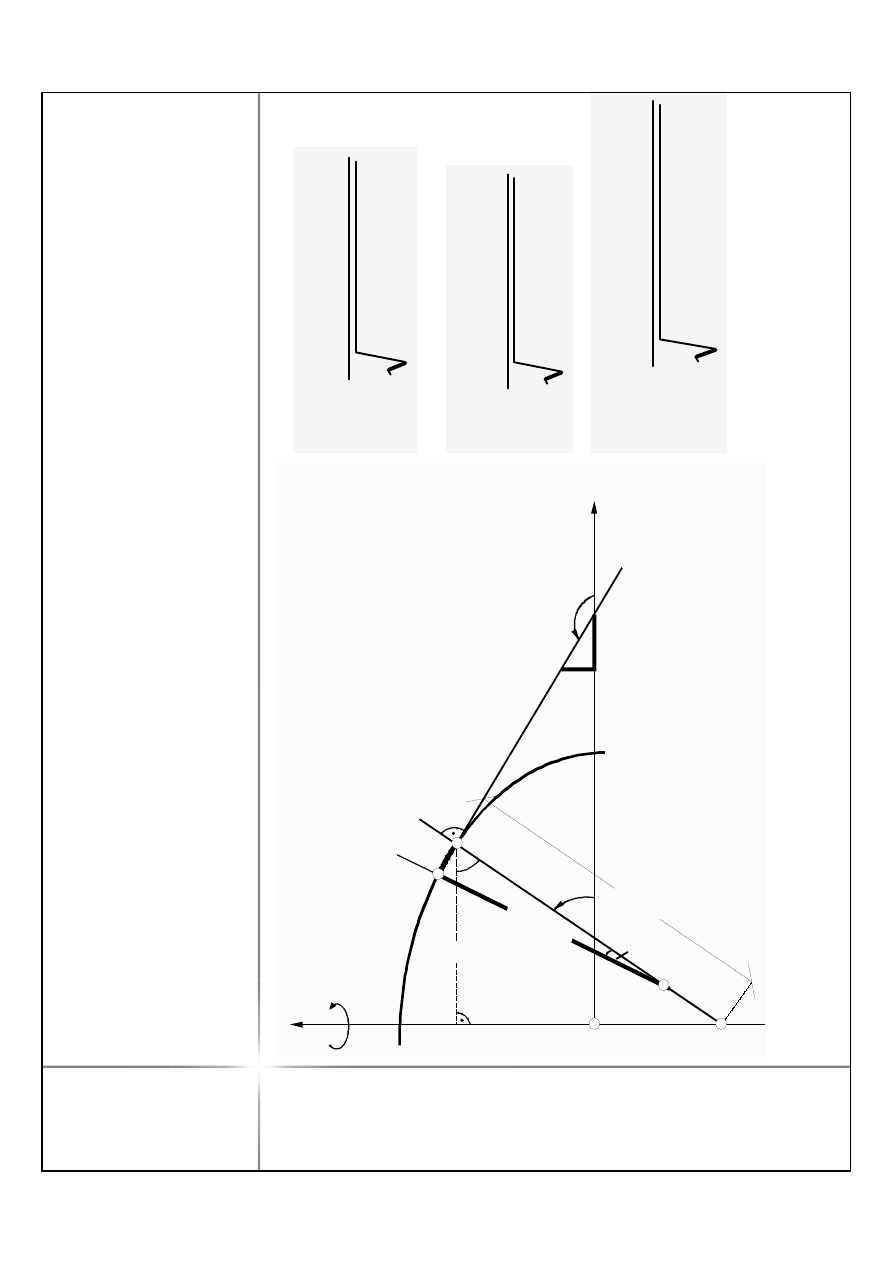
P

ro

m

id

P

ro

m

id

ń

ń

k

rz

y

w

iz

n

y

p

o

k

rz

y

w

iz

n

y

p

o

ł

ł

u

d

n

ik

a

u

d

n

ik

a

(2

)

(2

)

B

+

9

0

o

d

p

d

z

T

x/

y

P

B

d

s

P

'

p

B

d

B

O

O

p

M

N

ω

z

B

e

B

a

p

2

2

si

n

1

co

s

−

=

B

e

B

e

a

z

2

2

2

si

n

1

si

n
)

1(

−

−

=

3

2

2

2

)

si

n

1(

)

1(

B

e

e

a

M

−

−

=

(C

)

jw

(C

)

jw

9

9

/

3

2

/

3

2

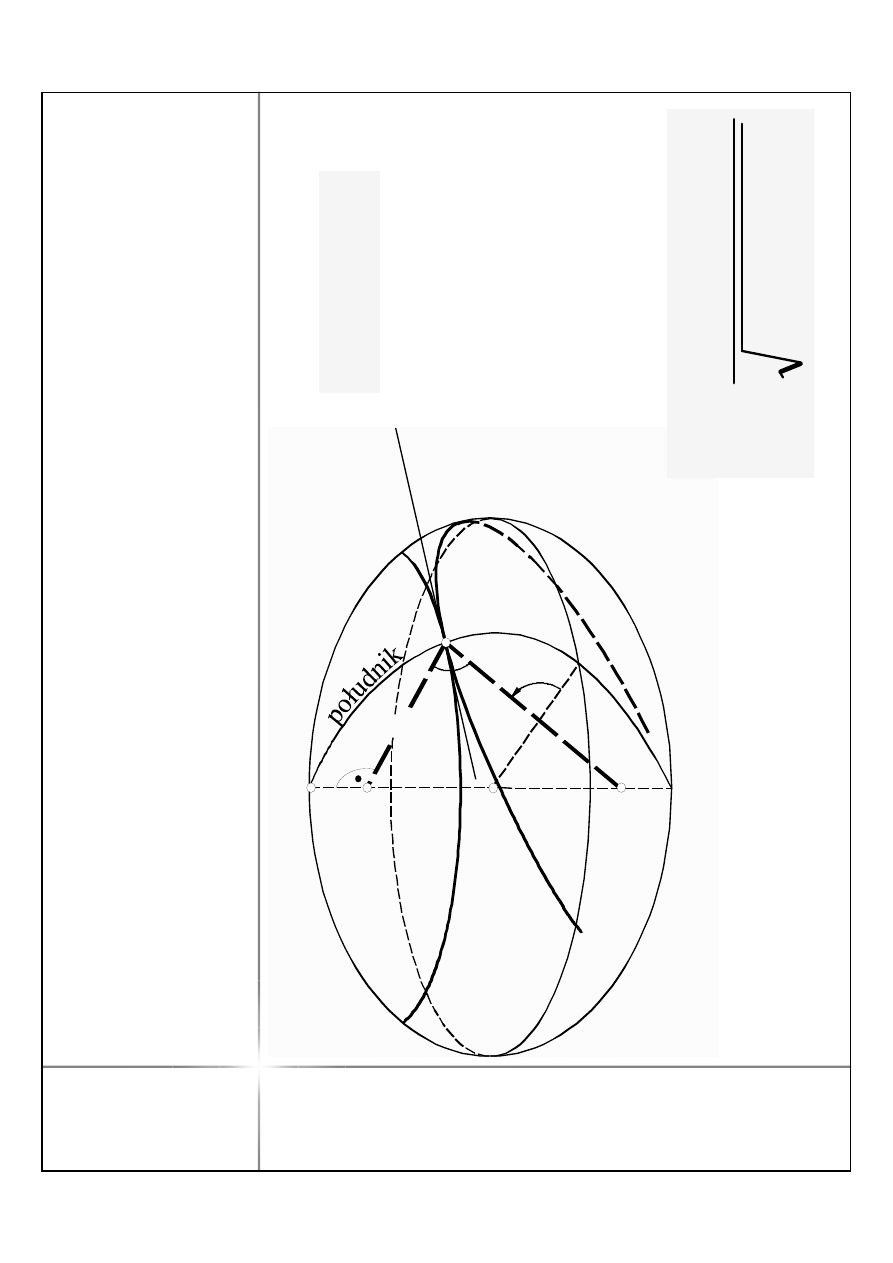
P

ro

m

id

P

ro

m

id

ń

ń

k

rz

y

w

iz

n

y

I

w

d

rt

y

k

a

k

rz

y

w

iz

n

y

I

w

d

rt

y

k

a

ł

ł

u

u

N

S

O

B

N

P

B

st

y

cz

n

a

ró

w

n

o

le

żn

ik

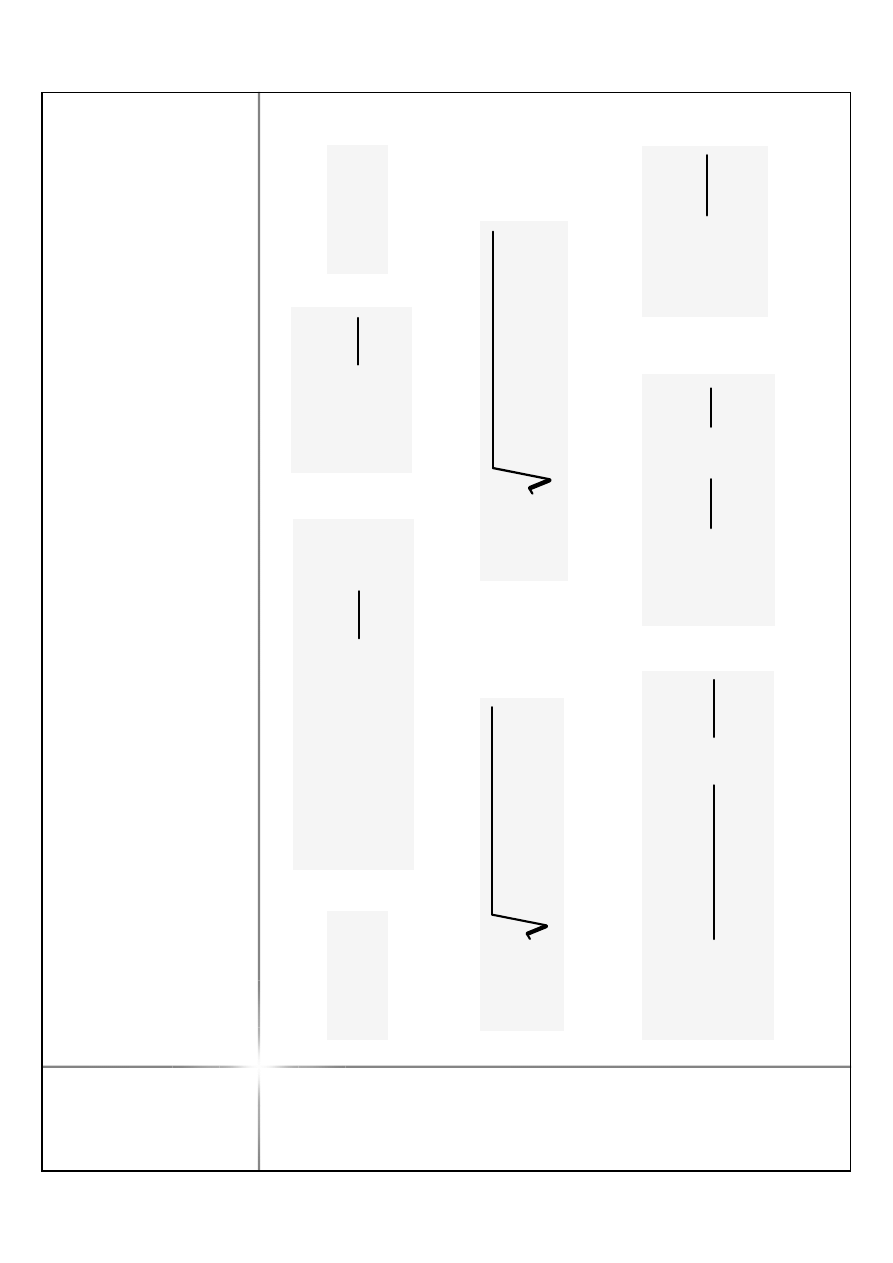
I

w

er

ty

ka

ł

p

B

e

a

N

2

2

si

n

1−

=

p

=

N

c

o

s

B

(C

)

jw

(C

)

jw

1

0

1

0

/

3

2

/

3

2

P

ro

m

id

n

id

d

li

p

s

o

id

y

o

b

ro

to

w

d

j

P

ro

m

id

n

id

d

li

p

s

o

id

y

o

b

ro

to

w

d

j

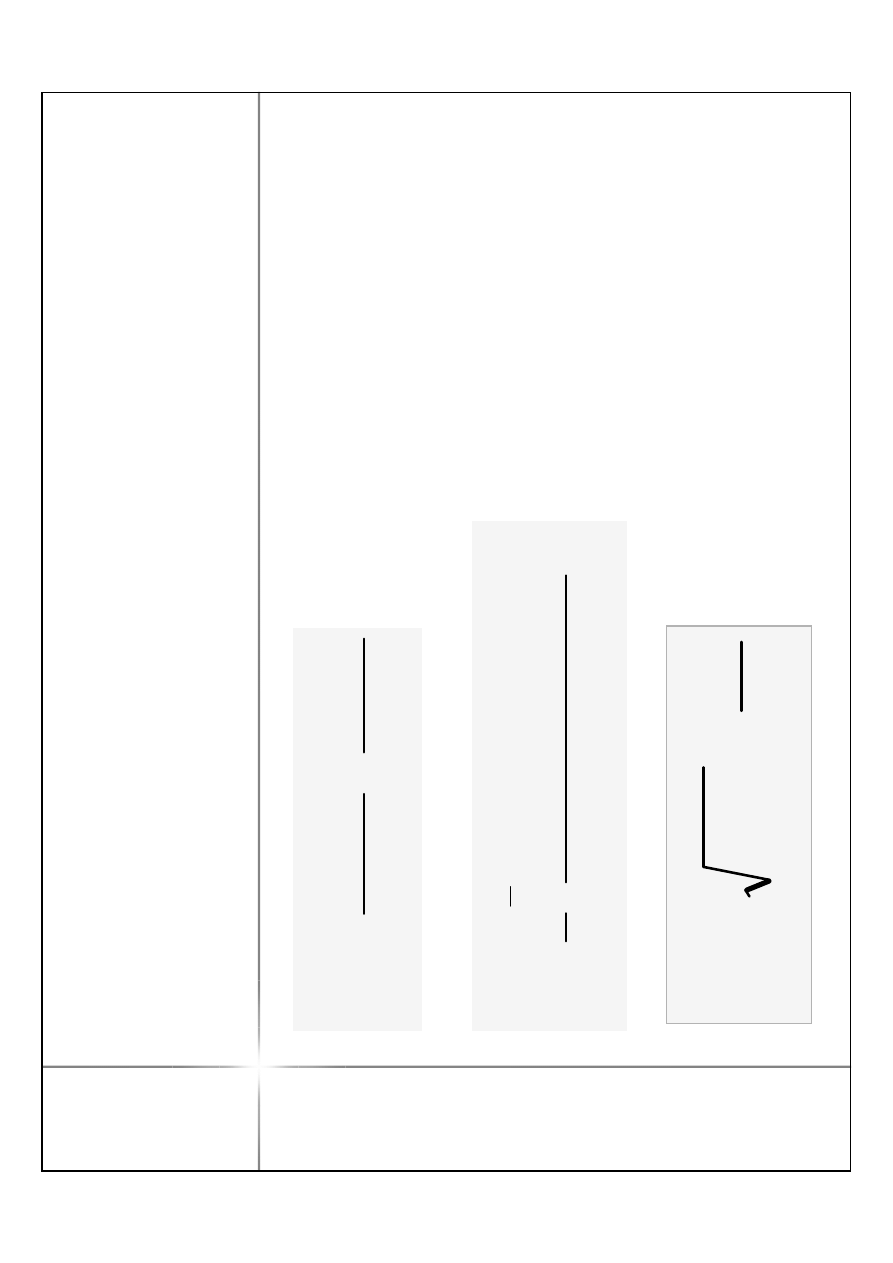
N

≥

M

a

b

M

2

0

=

N

0

=

a

c

b

a

N

M

=

=

=

2

90

90

B

e

W

2

2

si

n

1−
=

B

e

V

2

2

co

s

1

′

+
=

3

3

2

)

1(

V

c

W

e

a

M

=

−

=

V

c

W

a

N

=
=

2

V

N

M

=

(C

)

jw

(C

)

jw

1

1

1

1

/

3

2

/

3

2

Ś

Ś

rd

d

n

i

p

ro

m

id

rd

d

n

i

p

ro

m

id

ń

ń

k

rz

y

w

iz

n

y

k

rz

y

w

iz

n

y

N

A

M

A

R

A

2

2

1

si

n

co

s

+

=

−

T

w

ie

rd

ze

n

ie

E

u

le

ra

m

ó

w

i

o

t

y

m

,

że

k

rz

y

w

iz

n

ę

R

-1

d

o

w

o

ln

e

g

o

p

rz

e

k

ro

ju

n

o

rm

a

ln

e

g

o

o

a

zy

m

u

ci

e

A

m

o

żn

a

w

y

zn

a

cz

y

ć

n

a

p

o

d

st

a

w

ie

k

rz

y

w

iz

n

w

k

ie

ru

n

k

a

ch

g

łó

w

n

y

ch

N

-1

i

M

-1

∫

+

=

2

0

2

2

si

n

co

s

2

π

π

d

A

A

M

A

N

N
M

R

S

2

V

c

N
M

R

S

=

=

Ś

re

d

n

i

p

ro

m

ie

ń

w

p

u

n

k

ci

e

–

cz

ę

st

o

st

o

so

w

a

n

y

w

g

e

o

d

e

zj

i

w

y

ż

sz

e

j

d

o

ro

zw

ią

za

n

ia

z

a

d

a

ń

n

a

k

u

li

(C

)

jw

(C

)

jw

1

2

1

2

/

3

2

/

3

2

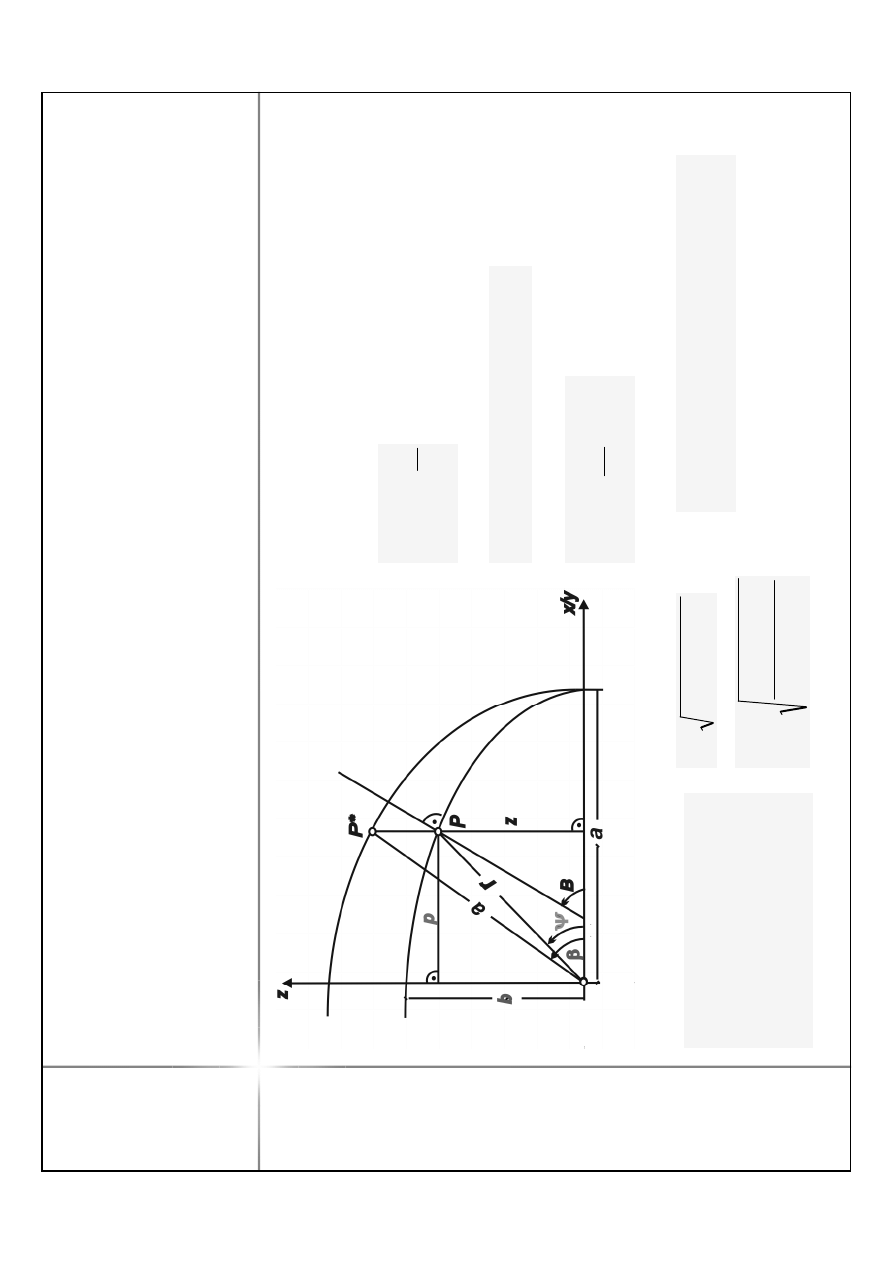
Z

m

ia

n

a

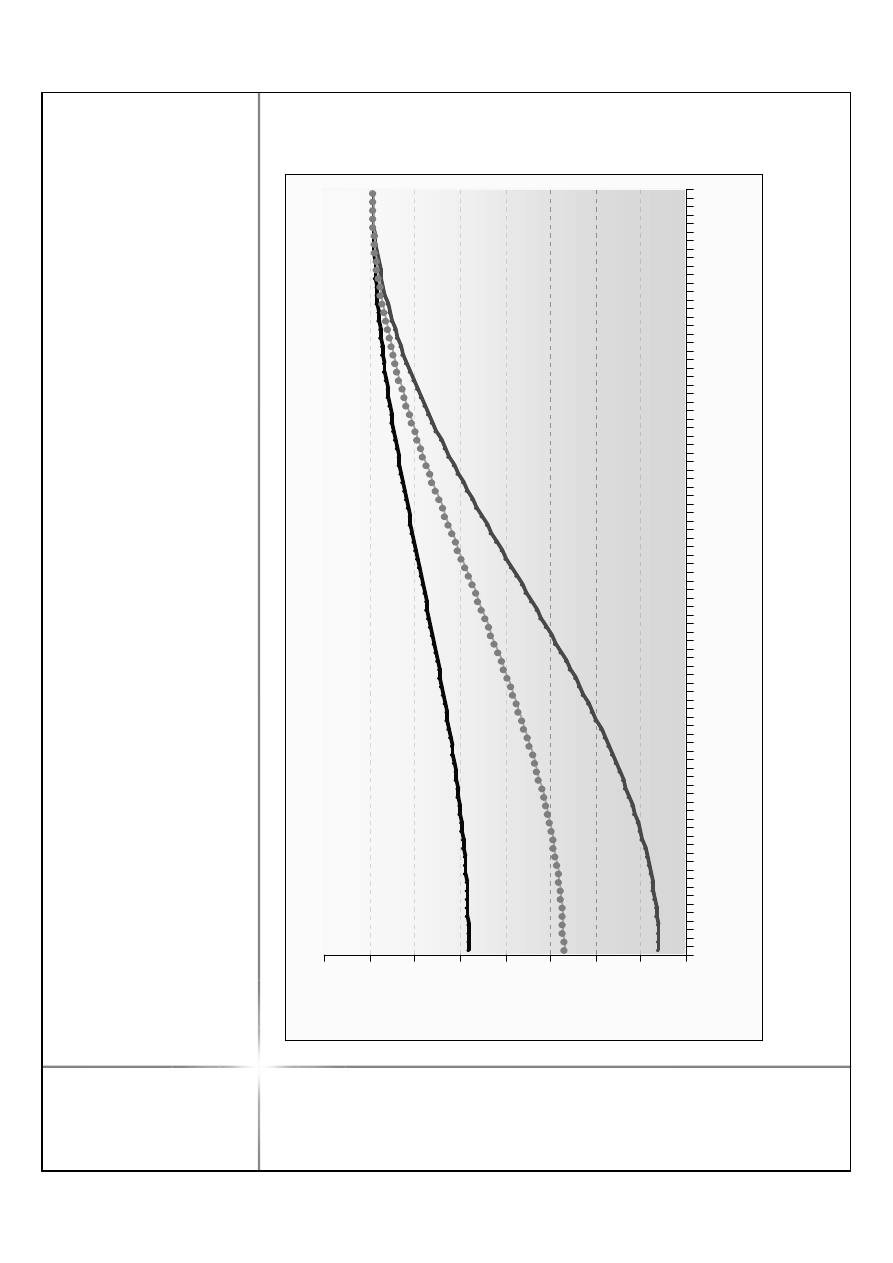
d

Z

m

ia

n

a

d

ł

ł

u

g

o

u

g

o

ś

ś

c

i

M,

N

i

R

c

i

M,

N

i

R

6

3

3

0

6

3

4

0

6

3

5

0

6

3

6

0

6

3

7

0

6

3

8

0

6

3

9

0

6

4

0

0

6

4

1

0

1

1

1

2

1

3

1

4

1

5

1

6

1

7

1

8

1

M

N

R

(C

)

jw

(C

)

jw

1

3

1

3

/

3

2

/

3

2

S

ze

ro

ko

S

ze

ro

ko

ś

ś

ci

g

eo

ce

n

tr

yc

zn

a

ci

g

eo

ce

n

tr

yc

zn

a

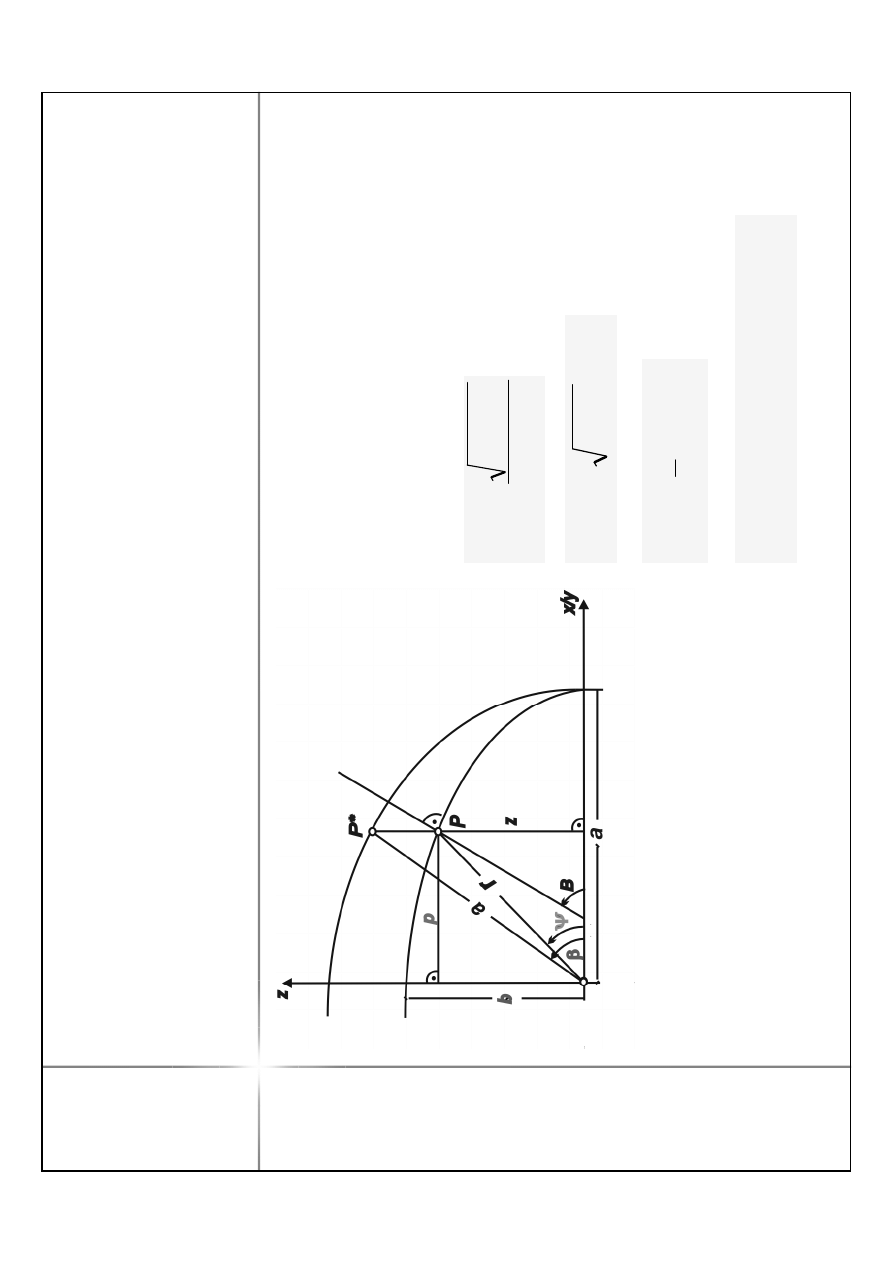
S

z

e

ro

k

o

ś

ć

g

e

o

c

e

n

tr

y

c

z

n

a

n

a

zy

w

a

m

y

k

ą

t

ψ

ja

k

i

tw

o

rz

y

p

ro

m

ie

ń

w

o

d

zą

cy

p

u

n

k

tu

P

p

o

ło

ż

o

n

e

g

o

n

a

e

lip

so

id

zi

e

z

p

ła

sz

cz

y

zn

ą

ró

w

n

ik

a

ta

nψ

=

z

p

ta

n

ψ

=

(

1

-

e

2

)

ta

n

B

x

y

z

r

L

L





  





  

=





  





  

co

s

co

s

co

s

co

s

si

n

ψ

ψ

ψ

r

x

y

z

=

+

+

2

2

2

r

a

e

e

=

−

−

1

1

2

2

2

co

s

ψ

B

e

B

−

≈

ψ

2

2

2
si

n

(

)

.

m

ax

(

)

B

B

o

−

≈

′

=

ψ

4

5

1

1

6

(C

)

jw

(C

)

jw

1

4

1

4

/

3

2

/

3

2

S

ze

ro

ko

S

ze

ro

ko

ś

ś

ci

z

re

d

u

ko

w

an

a

ci

z

re

d

u

ko

w

an

a

S

z

e

ro

k

o

ś

ć

z

re

d

u

k

o

w

a

n

ą

n

a

zy

w

a

m

y

k

ą

t

β

ja

k

i

tw

o

rz

y

p

ro

m

ie

ń

w

o

d

zą

cy

p

u

n

k

tu

P

*

p

o

ło

ż

o

n

e

g

o

n

a

s

fe

rz

e

z

p

ła

sz

cz

y

zn

ą

ró

w

n

ik

a

.

P

u

n

k

t

P

*

o

tr

zy

m

u

je

m

y

r

zu

tu

ją

c

p

u

n

k

t

P

z

e

lip

so

id

y

n

a

s

fe

rę

o

p

ro

m

ie

n

iu

a

p

ro

st

ą

ró

w

n

o

le

g

łą

d

o

o

si

O

Z

ta

nβ

=

−
a

p

p

2

2

B

e

ta

n

1

ta

n

2

−

=

β

B

e

B

−

≈

β

1

4

2

2

si

n

(

)

.

m

ax

(

)

B

B

o

−

≈

′

=

β

4

5

5

8

(C

)

jw

(C

)

jw

1

5

1

5

/

3

2

/

3

2

R

R

ó

ó

w

n

an

ia

p

ar

am

et

ry

cz

n

e

el

ip

so

id

y

o

b

ro

to

w

ej

w

n

an

ia

p

ar

am

et

ry

cz

n

e

el

ip

so

id

y

o

b

ro

to

w

ej

(1

)

(1

)

p

=

N

co

s

B

z

=

N

(1

-

e

2

)

si

n

B

y

=

p

si

n

L

x

=

p

co

s

L

x

y

z

N

B

L

B

L

B

e





  





  

=





  





  

=

−

−

−

co

s

co

s

co

s

si

n

si

n

,

,

τ

τ

1

1

2

1

W

ia

d

o

m

o

,

ż

e

:

o

ra

z

S

k

ą

d

p

a

ra

m

e

tr

y

cz

n

e

r

ó

w

n

a

n

ia

e

lip

so

id

y

o

b

ro

to

w

e

j

p

rz

y

jm

ą

p

o

st

a

ć

:

(C

)

jw

(C

)

jw

1

6

1

6

/

3

2

/

3

2

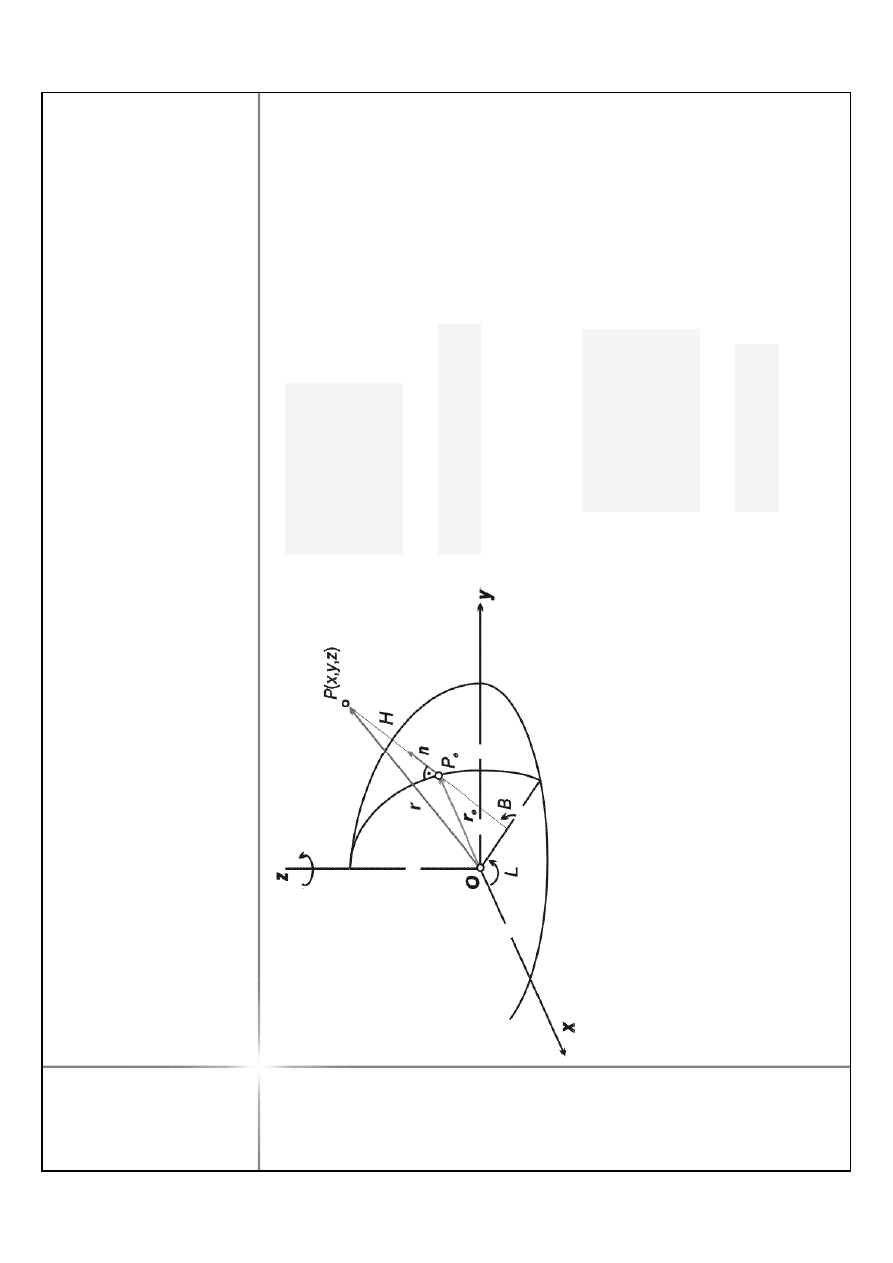
W

ek

to

r

n

o

rm

al

n

y

d

o

e

lip

so

id

y

o

b

ro

to

w

ej

W

ek

to

r

n

o

rm

al

n

y

d

o

e

lip

so

id

y

o

b

ro

to

w

ej

(

)

L

L

oy
n

L

n
ox

B

B

oz

n

o

sin

)

90

cos(

)
,

cos(

cos

)
,

cos(

sin

90

cos
)
,

cos(

n

n

y
n

n

n
x

z
n

′

=
−

′

=

′

=

⋅′

′

=

′

=′

⋅

=
−

=

=

⋅

D

e

fi

n

iu

ją

c

k

ie

ru

n

k

i

o

si

u

k

ła

d

u

p

ro

st

o

k

ą

tn

e

g

o

i

k

ie

ru

n

e

k

n

o

rm

a

ln

e

j

w

p

u

n

k

ci

e

p

rz

e

z

w

e

rs

o

ry

x

,

y

,

z

i

n

m

o

ż

e

m

y

z

a

p

is

a

ć

:

g

d

zi

e

n

’

to

r

zu

t

w

e

k

to

ra

n

n

a

p

ła

sz

cz

y

zn

ę

o

x

y

o

ra

z

ic

h

i

lo

cz

y

n

s

k

a

la

rn

y

:

(

)

B

n
n

co

s

)

,

co

s(

n

n
n

′

=

′

=

⋅′

M

n

o

żą

c

st

ro

n

a

m

i

d

w

a

o

st

a

tn

ie

r

ó

w

n

a

n

ia

w

zo

ru

(

*

)

p

rz

e

z

ró

w

n

a

n

ie

(

*

*

)

d

o

st

a

je

m

y

o

st

a

te

cz

n

ie

z

a

le

ż

n

o

ś

ci

n

a

w

e

k

to

r

n

o

rm

a

ln

y

d

o

e

lip

so

id

y

o

b

ro

to

w

e

j.

(*

)

(*

*

)

(C

)

jw

(C

)

jw

1

7

1

7

/

3

2

/

3

2

R

R

ó

ó

w

n

an

ia

p

ar

am

et

ry

cz

n

e

el

ip

so

id

y

o

b

ro

to

w

ej

w

n

an

ia

p

ar

am

et

ry

cz

n

e

el

ip

so

id

y

o

b

ro

to

w

ej

(2

)

(2

)





















=

B

L

B

L

B

sin

sin

cos

cos

cos

n

F

=

d

ia

g

(1

,

1

,

τ)

n
F

r

1

−

=





















=

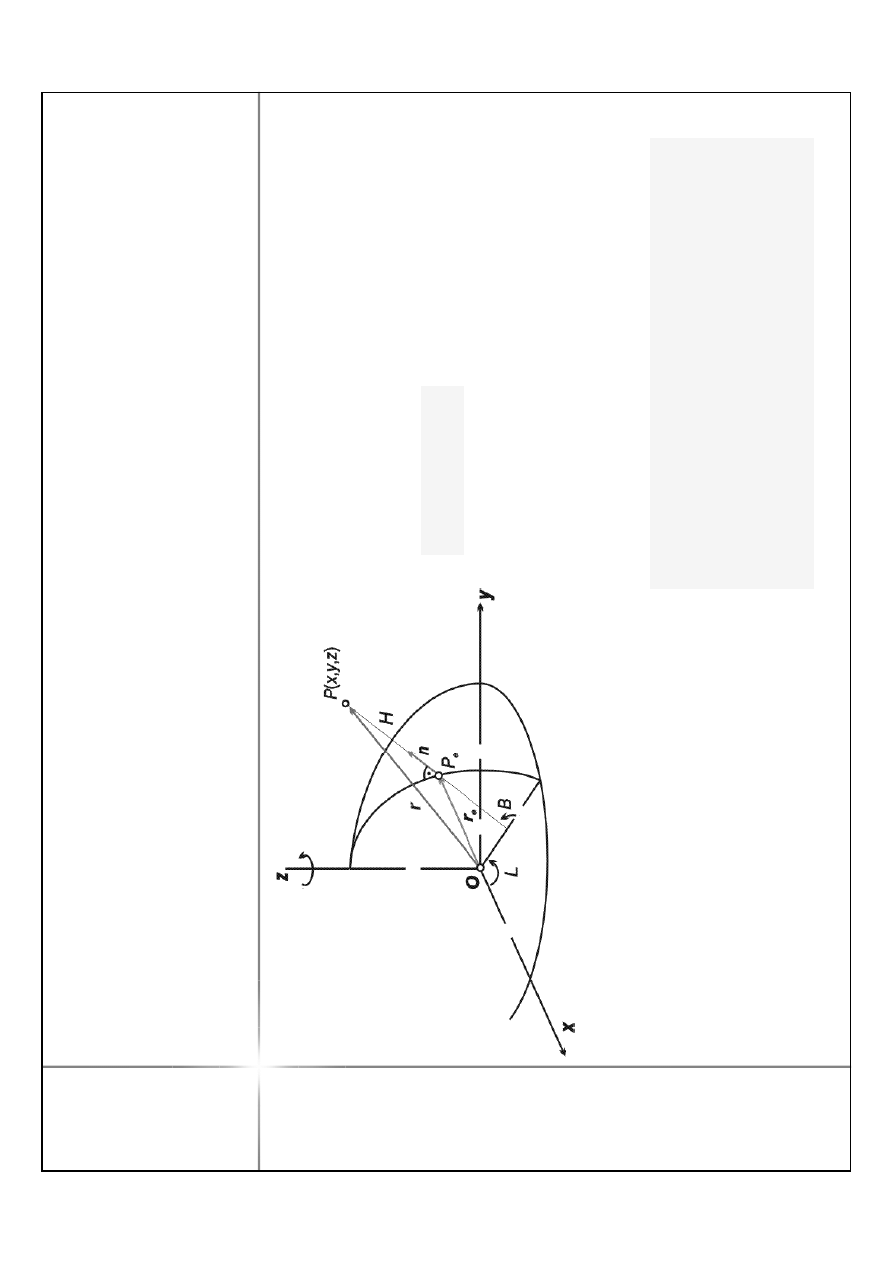
N

z

y

x

e

r

=

r

e

+

n

H

W

e

k

to

r

n

o

rm

a

ln

y

d

o

e

lip

so

id

y

D

ia

g

o

n

a

ln

a

m

a

ci

e

rz

k

sz

ta

łt

u

(C

)

jw

(C

)

jw

1

8

1

8

/

3

2

/

3

2

R

R

ó

ó

w

n

an

ia

p

ar

am

et

ry

cz

n

e

el

ip

so

id

y

o

b

ro

to

w

ej

w

n

an

ia

p

ar

am

et

ry

cz

n

e

el

ip

so

id

y

o

b

ro

to

w

ej

(3

)

(3

)

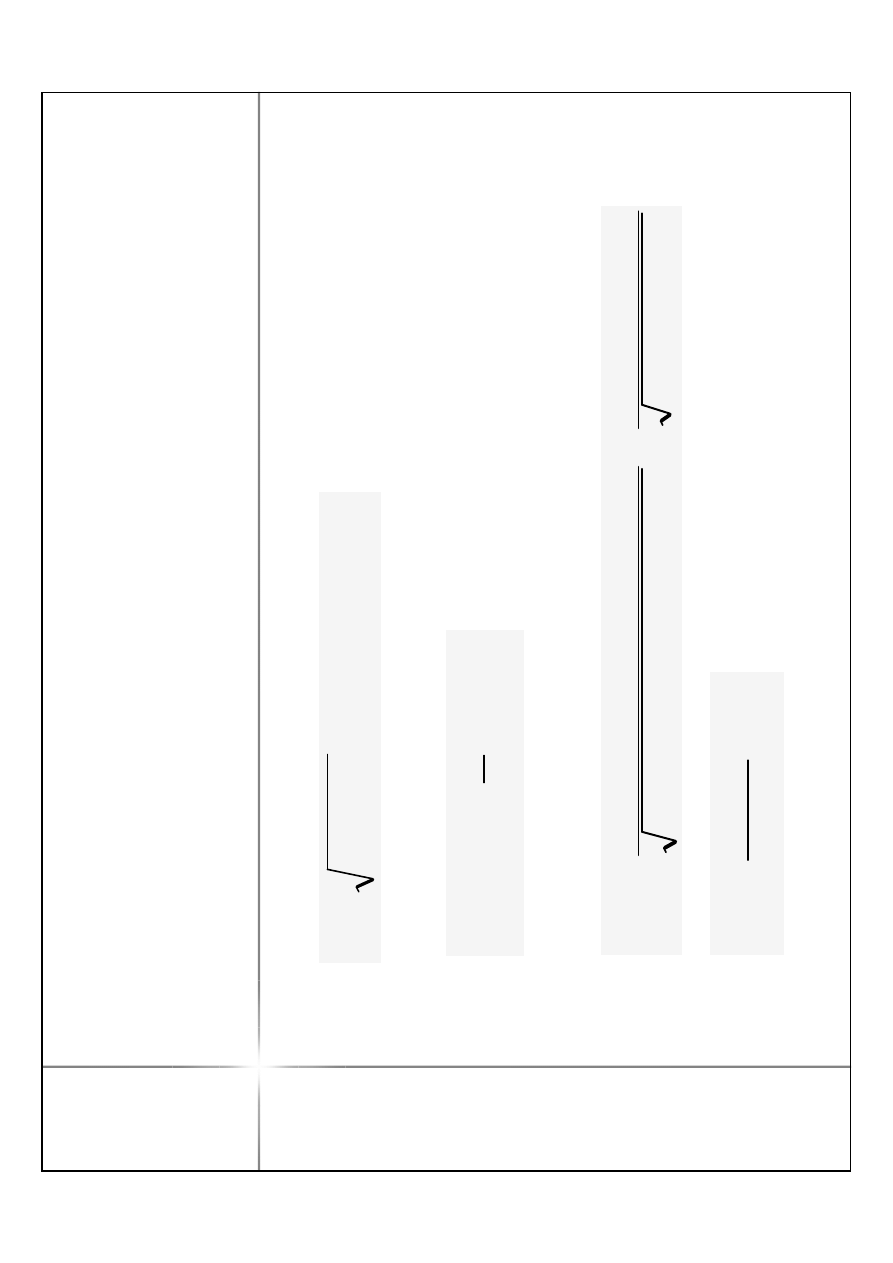
W

e

k

to

r

w

o

d

zą

cy

p

u

n

k

tu

n

a

f

.p

.Z

.

w

f

u

n

k

cj

i

w

sp

ó

łr

zę

d

n

y

ch

g

e

o

d

e

zy

jn

y

ch

(

)
(

)





















+

−

+

+

= 



















=

B

H

e

N

L

B

H

N

L

B

H

N

z

y

x

si

n

1

si

n

co

s

)

(

co

s

co

s

)

(

2

r

r

=

r

e

+

n

H

(C

)

jw

(C

)

jw

1

9

1

9

/

3

2

/

3

2

M

et

o

d

a

M

et

o

d

a

H

ir

vo

n

en

a

H

ir

vo

n

en

a

–

–

p

rz

el

ic

ze

n

ie

(

p

rz

el

ic

ze

n

ie

(

xy

z

xy

z

-

-

>

B

L

H

)

(1

)

>

B

L

H

)

(1

)

B

H

N

y

x

p

co

s

)

(

2

2

+

=

+

=

(

)

1

2

)

0

(

1

ta

n

−

=

−

=

e

p

z

B

k

N

a

e

B

B

a

e

B

k

k

k

k

(

)

(

)

(

)

(

)

(

)

s

in

c

o

s

s

in

=

−

+

=

−

1

1

2

2

2

2

2

)
(

)
(

)
(

co

s

k

k

k

N

B

p

H

−

=

1.

O

b

lic

za

m

y

:

2.

L

ic

zy

m

y

p

ie

rw

sz

e

p

rz

yb

liż

en

ie

B

:

3.

O

b

lic

za

m

y

N

i

H

d

la

a

kt

u

al

n

ej

w

ar

to

śc

i B

:

(C

)

jw

(C

)

jw

2

0

2

0

/

3

2

/

3

2

M

et

o

d

a

M

et

o

d

a

H

ir

vo

n

en

a

H

ir

vo

n

en

a

–

–

p

rz

el

ic

ze

n

ie

(

p

rz

el

ic

ze

n

ie

(

xy

z

xy

z

-

-

>

B

L

H

)

(2

)

>

B

L

H

)

(2

)

 

 



 

 



 



 



+

−

=

−

−

+

1

)
(

)
(

)
(

2

1

)

1

(

1

ta

n

k

k

k

k

H

N

N

e

p

z

B

B

B

k

k

(

)

+

−

<

1

ε

1

0000,

0

′′

=

ε

4.

L

ic

zy

m

y

ko

le

jn

e

p

rz

yb

liż

en

ie

B

:

5.

S

p

ra

w

d

za

m

y,

c

zy

s

p

eł

n

io

n

y

je

st

w

ar

u

n

ek

:

gdz

ie

n

p

.:

(C

)

jw

(C

)

jw

2

1

2

1

/

3

2

/

3

2

M

et

o

d

a

M

et

o

d

a

H

ir

vo

n

en

a

H

ir

vo

n

en

a

–

–

p

rz

el

ic

ze

n

ie

(

p

rz

el

ic

ze

n

ie

(

xy

z

xy

z

-

-

>

B

L

H

)

(3

)

>

B

L

H

)

(3

)

 



 



=

−

x

y

L

1

tan

N

a

e

B

=

−

1

2

2

s

in

N

B

p

H

−

=

co

s

Je

śl

i w

ar

u

n

ek

n

ie

je

st

s

p

eł

n

io

n

y

to

w

ra

ca

m

y

d

o

p

u

n

kt

u

3

, w

p

rz

ec

iw

n

ym

w

yp

ad

ku

o

b

lic

za

m

y

o

st

at

ec

zn

e

w

ar

to

śc

i L

, N

i

H

d

la

o

st

at

n

ie

j w

ar

to

śc

i B

(C

)

jw

(C

)

jw

2

2

2

2

/

3

2

/

3

2

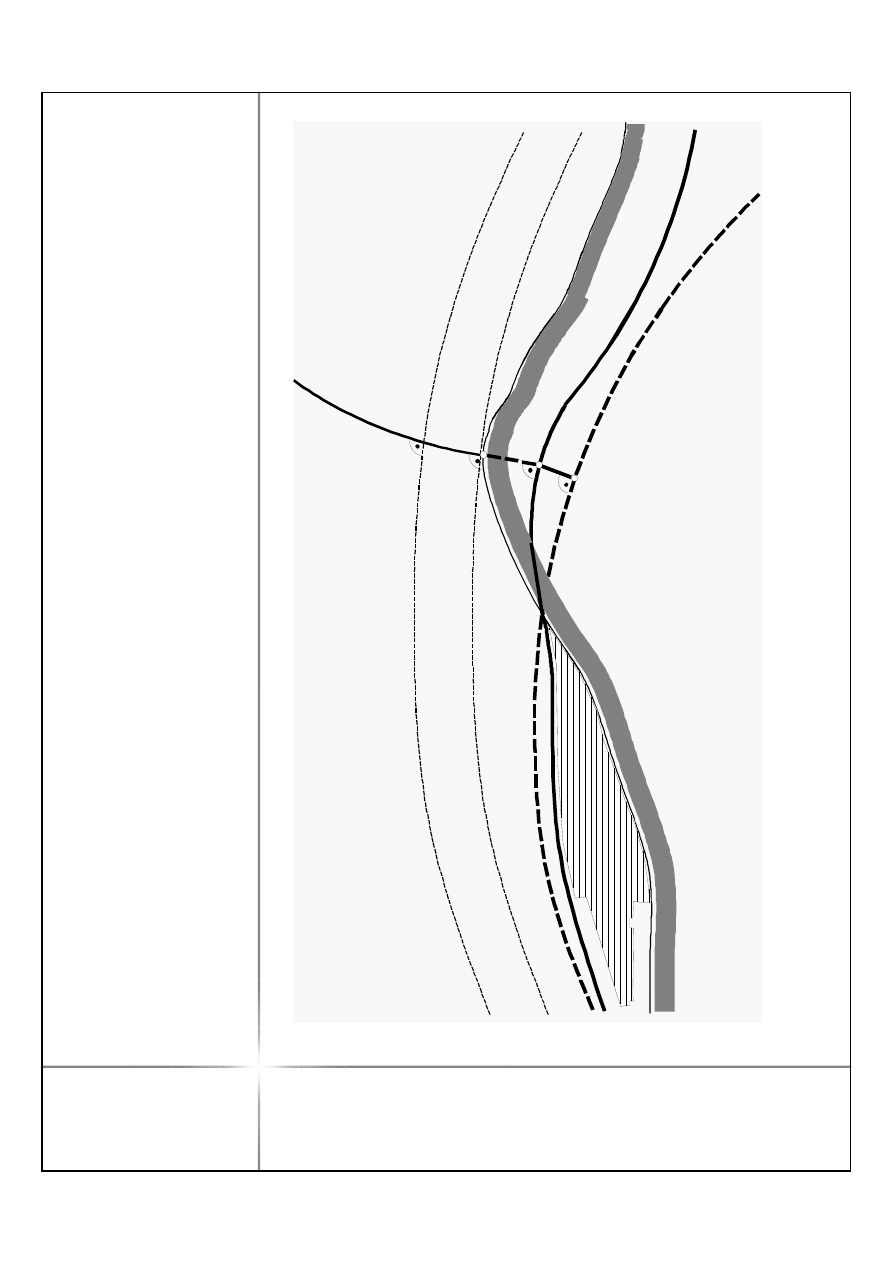
W

a

W

a

ż

ż

n

ie

js

n

e

k

rn

y

w

e

g

e

o

d

e

n

y

jn

e

n

a

n

ie

js

n

e

k

rn

y

w

e

g

e

o

d

e

n

y

jn

e

n

a

e

li

p

s

o

id

n

ie

o

b

ro

to

w

e

j

e

li

p

s

o

id

n

ie

o

b

ro

to

w

e

j

W

z

a

g

a

d

n

ie

n

ia

ch

ra

ch

u

n

k

o

w

y

ch

g

e

o

d

e

zj

i

w

y

r

W

z

a

g

a

d

n

ie

n

ia

ch

ra

ch

u

n

k

o

w

y

ch

g

e

o

d

e

zj

i

w

y

r

ó

ó

ż

ż

n

ia

s

i

n

ia

s

i

ę

ę

zw

y

k

le

t

rz

y

zw

y

k

le

t

rz

y

p

o

d

st

a

w

o

w

e

k

rz

y

w

e

n

a

e

lip

so

id

zi

e

o

b

ro

to

w

e

j:

p

o

d

st

a

w

o

w

e

k

rz

y

w

e

n

a

e

lip

so

id

zi

e

o

b

ro

to

w

e

j:

–

–

E

lip

sa

w

ie

lk

a

E

lip

sa

w

ie

lk

a

(a

n

a

lo

g

ia

d

o

k

o

(a

n

a

lo

g

ia

d

o

k

o

ł

ł

a

w

ie

lk

ie

g

o

)

a

w

ie

lk

ie

g

o

)

–

–

k

rz

y

w

a

p

k

rz

y

w

a

p

ł

ł

a

sk

a

a

sk

a

łą

łą

cz

cz

ą

ą

ca

j

e

d

n

o

zn

a

cz

n

ie

ca

j

e

d

n

o

zn

a

cz

n

ie

d

w

a

p

u

n

k

ty

n

a

p

o

w

ie

rz

ch

n

i

e

lip

so

id

y

i

l

e

d

w

a

p

u

n

k

ty

n

a

p

o

w

ie

rz

ch

n

i

e

lip

so

id

y

i

l

e

ż

ą

ż

ą

ca

w

p

ca

w

p

ł

ł

a

sz

cz

y

a

sz

cz

y

ź

ź

n

ie

z

a

w

ie

ra

j

n

ie

z

a

w

ie

ra

j

ą

ą

ce

j

ce

j

ś

ś

ro

d

e

k

ro

d

e

k

e

lip

so

id

y

.

e

lip

so

id

y

.

–

–

P

rz

e

k

ro

je

n

o

rm

a

ln

e

w

za

je

m

n

e

P

rz

e

k

ro

je

n

o

rm

a

ln

e

w

za

je

m

n

e

–

–

k

rz

y

w

a

p

k

rz

y

w

a

p

ł

ł

a

sk

a

n

a

p

o

w

ie

rz

ch

n

i

e

lip

so

id

y

a

sk

a

n

a

p

o

w

ie

rz

ch

n

i

e

lip

so

id

y

łą

łą

cz

cz

ą

ą

ca

ca

d

w

a

p

u

n

k

ty

i

l

e

d

w

a

p

u

n

k

ty

i

l

e

ż

ą

ż

ą

ca

w

p

ca

w

p

ł

ł

a

sz

cz

y

a

sz

cz

y

ź

ź

n

ie

z

w

ie

ra

j

n

ie

z

w

ie

ra

j

ą

ą

ce

j

n

o

rm

a

ln

ce

j

n

o

rm

a

ln

ą

ą

d

o

e

lip

so

id

y

w

p

u

n

k

ci

e

d

o

e

lip

so

id

y

w

p

u

n

k

ci

e

p

o

cz

p

o

cz

ą

ą

tk

o

w

y

m

.

P

rz

e

k

ro

je

n

o

rm

a

ln

e

w

za

je

m

n

e

tk

o

w

y

m

.

P

rz

e

k

ro

je

n

o

rm

a

ln

e

w

za

je

m

n

e

n

ie

p

o

k

ry

w

a

j

n

ie

p

o

k

ry

w

a

j

ą

ą

s

i

s

i

ę

ę

ze

s

o

b

ze

s

o

b

ą

ą

ze

w

zg

l

ze

w

zg

l

ę

ę

d

u

d

u

n

a

w

ic

h

ro

w

a

to

n

a

w

ic

h

ro

w

a

to

ś

ć

ś

ć

n

o

rm

a

ln

y

ch

i

w

o

g

n

o

rm

a

ln

y

ch

i

w

o

g

ó

ó

ln

y

m

p

rz

y

p

a

d

k

u

(

p

o

za

r

ln

y

m

p

rz

y

p

a

d

k

u

(

p

o

za

r

ó

ó

w

n

ik

ie

m

i

p

o

w

n

ik

ie

m

i

p

o

ł

ł

u

d

n

ik

a

m

i)

u

d

n

ik

a

m

i)

p

o

m

i

p

o

m

i

ę

ę

d

zy

d

w

o

m

a

p

u

n

k

ta

m

i

m

o

d

zy

d

w

o

m

a

p

u

n

k

ta

m

i

m

o

ż

ż

n

a

p

o

p

ro

w

a

d

zi

n

a

p

o

p

ro

w

a

d

zi

ć

ć

d

w

a

p

rz

e

k

ro

je

n

o

rm

a

ln

e

w

za

je

m

n

e

.

d

w

a

p

rz

e

k

ro

je

n

o

rm

a

ln

e

w

za

je

m

n

e

.

–

–

L

in

ia

g

e

o

d

e

zy

jn

a

(

o

rt

o

d

ro

m

a

)

L

in

ia

g

e

o

d

e

zy

jn

a

(

o

rt

o

d

ro

m

a

)

–

–

n

a

jk

r

n

a

jk

r

ó

ó

ts

z

a

i

j

e

d

n

o

z

n

a

c

z

n

a

ts

z

a

i

j

e

d

n

o

z

n

a

c

z

n

a

lin

ia

lin

ia

łą

łą

cz

cz

ą

ą

ca

d

w

a

ca

d

w

a

p

u

n

k

ty

n

a

p

o

w

ie

rz

ch

n

i.

M

a

te

m

a

ty

cz

n

ie

l

in

ia

g

e

o

d

e

zy

jn

a

t

o

t

a

k

a

l

i

p

u

n

k

ty

n

a

p

o

w

ie

rz

ch

n

i.

M

a

te

m

a

ty

cz

n

ie

l

in

ia

g

e

o

d

e

zy

jn

a

t

o

t

a

k

a

l

i

n

ia

,

k

t

n

ia

,

k

t

ó

ó

re

j

n

o

rm

a

ln

a

re

j

n

o

rm

a

ln

a

g

g

ł

ł

ó

ó

w

n

a

w

k

a

w

n

a

w

k

a

ż

ż

d

y

m

p

u

n

k

ci

e

m

a

k

ie

ru

n

e

k

n

o

rm

a

ln

e

j

d

o

p

o

w

ie

rz

ch

n

i

(e

lip

so

id

y

).

d

y

m

p

u

n

k

ci

e

m

a

k

ie

ru

n

e

k

n

o

rm

a

ln

e

j

d

o

p

o

w

ie

rz

ch

n

i

(e

lip

so

id

y

).

(C

)

jw

(C

)

jw

2

3

2

3

/

3

2

/

3

2

L

in

ia

g

e

o

d

e

n

y

jn

a

L

in

ia

g

e

o

d

e

n

y

jn

a

0

1

2

3

2

2

2

=

 



 



+

 



 



−

+

dB

dL

dB

dp

M

p

dB

dL

dB

dM

M

dB

dp

p

dL

B
d

0

)

(

=

⋅′′

×′
=

n

r

r

g

κ

R

ó

w

n

a

n

ie

l

in

ii

g

e

o

d

e

z

y

jn

e

j

m

o

ż

n

a

z

a

p

is

a

ć

p

o

p

rz

e

z

w

a

ru

n

e

k

z

e

ro

w

e

j

w

a

rt

o

ś

c

i

k

rz

y

w

iz

n

y

g

e

o

d

e

z

y

jn

e

j

(k

rz

y

w

iz

n

a

r

zu

tu

p

ro

st

o

k

ą

tn

e

g

o

k

rz

y

w

e

j

n

a

p

ła

sz

cz

y

zn

ę

st

y

cz

n

ą

d

o

p

o

w

ie

rz

ch

n

i)

:

g

d

zi

e

r’

o

zn

a

cz

a

w

e

k

to

r

st

y

cz

n

y

d

o

p

o

w

ie

rz

ch

n

i,

r”

w

e

k

to

r

k

rz

y

w

iz

n

y

,

a

n

w

e

k

to

r

n

o

rm

a

ln

y

d

o

p

o

w

ie

rz

ch

n

i.

P

o

w

st

a

w

ie

n

iu

d

la

e

lip

so

id

y

w

sp

ó

łr

zę

d

n

y

ch

g

e

o

d

e

zy

jn

y

ch

B

i

L

d

o

st

a

n

ie

m

y

ró

w

n

a

n

ie

r

ó

ż

n

ic

zk

o

w

e

d

ru

g

ie

g

o

r

zę

d

u

p

o

st

a

ci

:

(*

)

(C

)

jw

(C

)

jw

2

4

2

4

/

3

2

/

3

2

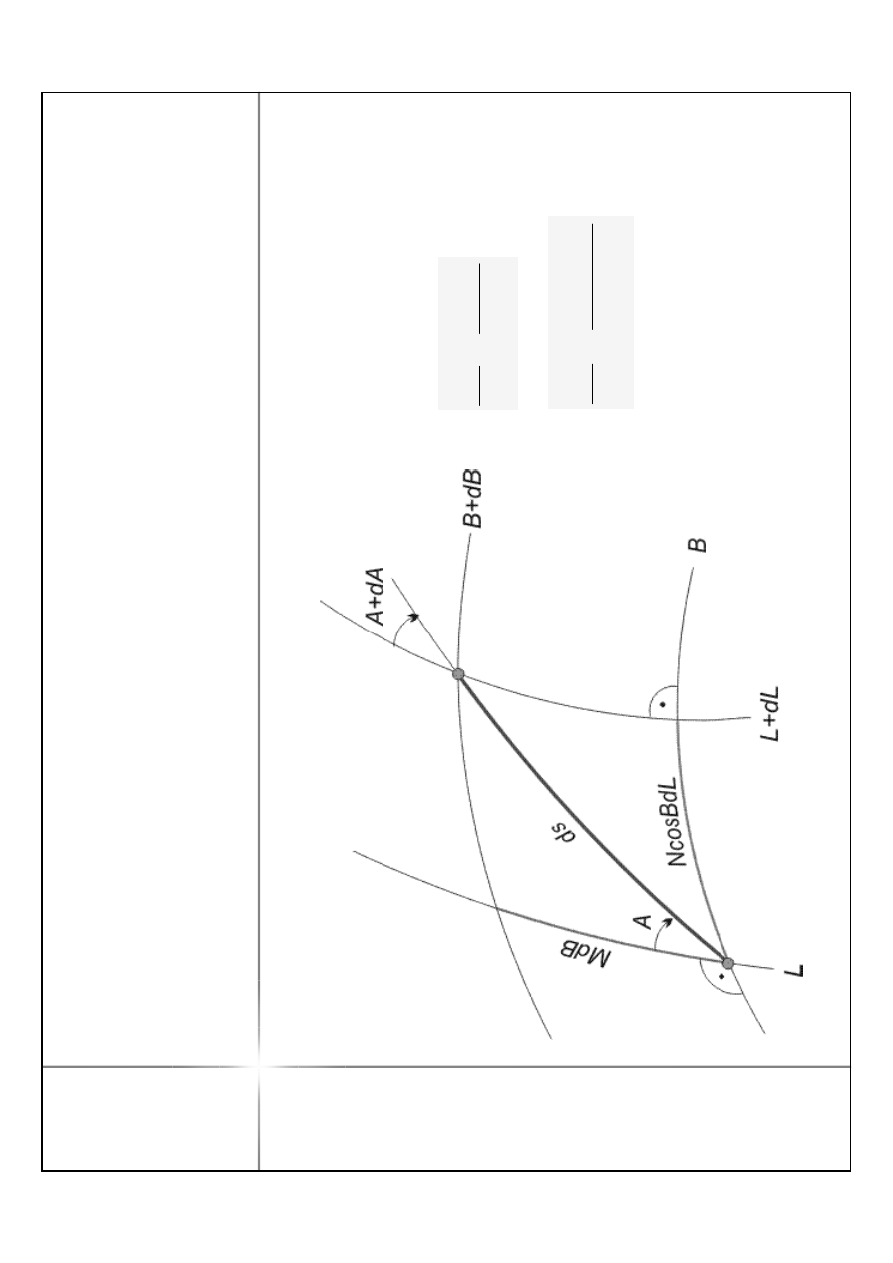
P

o

d

s

ta

w

o

w

e

r

P

o

d

s

ta

w

o

w

e

r

ó

ó

w

n

a

n

ia

r

w

n

a

n

ia

r

ó

ó

ż

ż

n

ic

n

k

o

w

e

n

ic

n

k

o

w

e

p

ie

rw

s

n

e

g

o

r

n

p

ie

rw

s

n

e

g

o

r

n

ę

ę

d

u

l

in

ii

g

e

o

d

e

n

y

jn

e

j

d

u

l

in

ii

g

e

o

d

e

n

y

jn

e

j

M

A

ds

dB

co

s

=

B

N

A

ds

dL

co

s

si

n

=

(C

)

jw

(C

)

jw

2

5

2

5

/

3

2

/

3

2

R

R

ó

ó

w

n

a

n

ie

w

n

a

n

ie

C

la

ir

a

u

n

ta

C

la

ir

a

u

n

ta

li

n

ii

g

e

o

d

e

n

y

jn

e

j

li

n

ii

g

e

o

d

e

n

y

jn

e

j

C

a

łk

o

w

a

n

ie

r

ó

w

n

a

n

ia

(

*

)

p

ro

w

a

d

zi

d

o

z

a

le

ż

n

o

ś

ci

:

co

n

st

c

A

B

N

=
=

⋅

⋅

si

n

co

s

R

ó

w

n

a

n

ie

C

la

ir

a

u

n

ta

w

y

ra

ż

a

w

ła

sn

o

ść

lin

ii

g

e

o

d

e

zy

jn

e

j

m

ó

w

ią

cą

o

t

y

m

,

ż

e

i

lo

cz

y

n

p

ro

m

ie

n

ia

r

ó

w

n

o

le

ż

n

ik

a

i

s

in

u

sa

a

zy

m

u

tu

l

in

ii

g

e

o

d

e

zy

jn

e

j

je

st

w

ie

lk

o

ś

ci

ą

st

a

łą

d

la

c

a

łe

j

lin

ii.

S

ta

łą

c

m

o

ż

n

a

i

n

te

rp

re

to

w

a

ć

ja

k

o

p

ro

m

ie

ń

ta

k

ie

g

o

r

ó

w

n

o

le

ż

n

ik

a

,

d

o

k

tó

re

g

o

l

in

ia

g

e

o

d

e

zy

jn

a

j

e

st

s

ty

cz

n

a

,

a

j

e

j

a

zy

m

u

t

w

y

n

o

si

9

0

o

.

W

f

u

n

k

cj

i

sz

e

ro

k

o

ś

ci

z

re

d

u

k

o

w

a

n

e

j

ró

w

n

a

n

ie

p

rz

y

jm

ie

p

o

st

a

ć

:

co

n

st

c

A

a

=
=

⋅

⋅

si

n

co

sβ

(C

)

jw

(C

)

jw

2

6

2

6

/

3

2

/

3

2

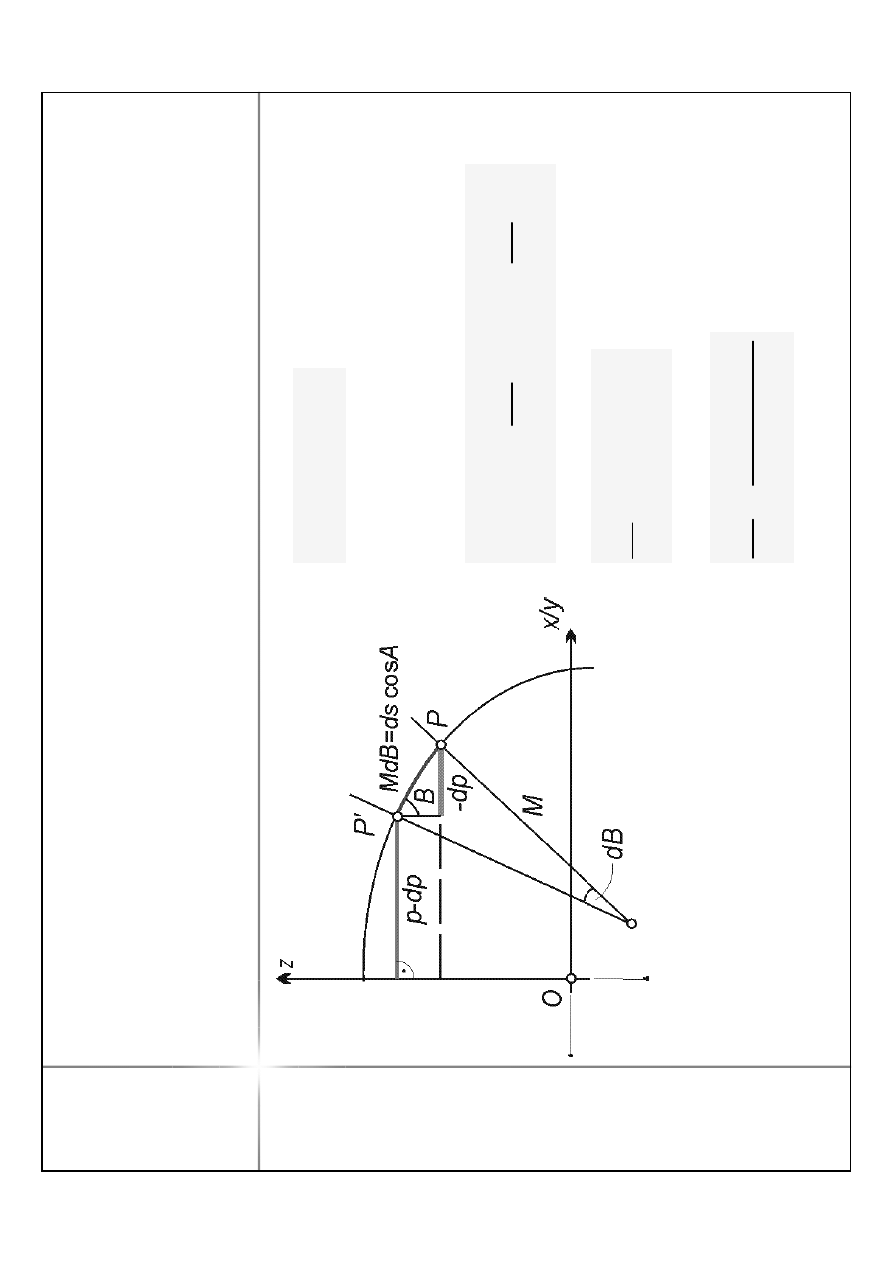
R

R

ó

ó

w

n

a

n

ie

r

w

n

a

n

ie

r

ó

ó

ż

ż

n

ic

n

k

o

w

e

p

ie

rw

s

n

e

g

o

n

ic

n

k

o

w

e

p

ie

rw

s

n

e

g

o

rn

rn

ę

ę

d

u

d

la

a

n

y

m

u

tu

d

u

d

la

a

n

y

m

u

tu

B

A

ds

dp

si

n

co

s

⋅

=

N

B

A

ds

dA

ta

n

si

n

⋅

=

c

A

p

=

⋅s

in

0

si

n

co

s

=

⋅

−

⋅

⋅

d

s

d

p

A

d

s

d

A

A

p

R

ó

ż

n

ic

zk

u

ją

c

ró

w

n

a

n

ie

C

la

ir

a

u

n

ta

p

o

p

a

ra

m

e

tr

ze

n

a

tu

ra

ln

y

m

s

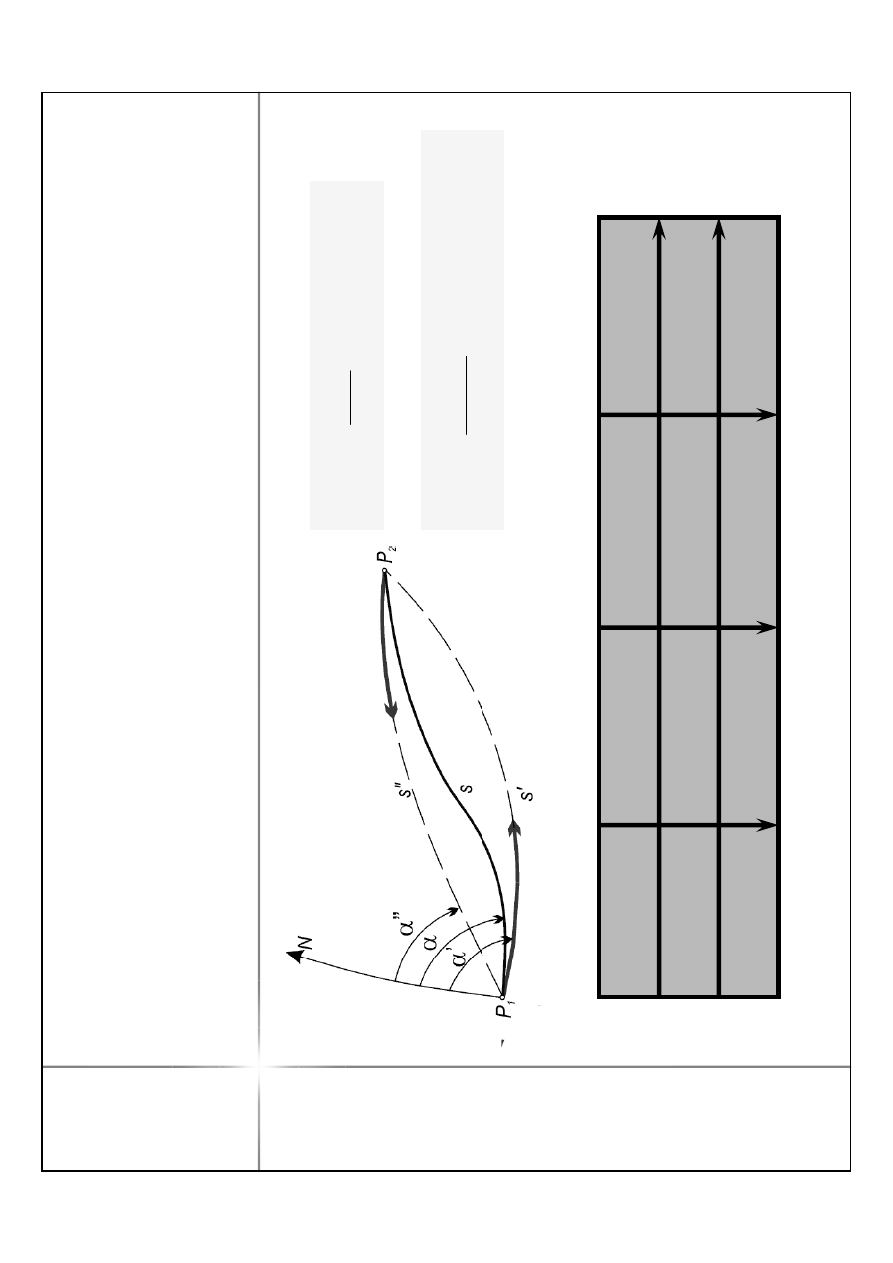
R

ó

w

n

a

n

ie

r

ó

ż

n

ic

zk

o

w

e

d

la

a

zy

m

u

tu

:

(C

)

jw

(C

)

jw

2

7

2

7

/

3

2

/

3

2

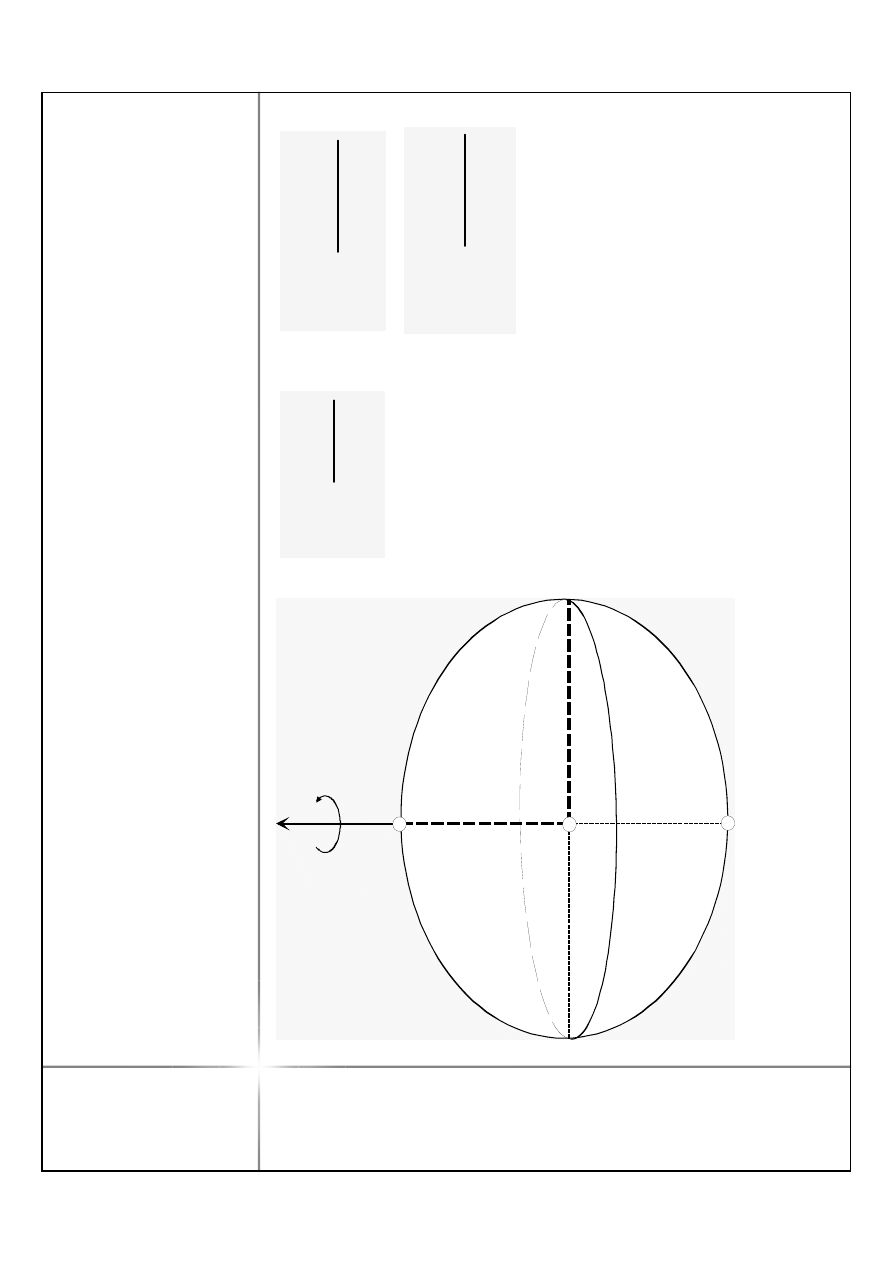
W

n

a

je

m

n

e

p

rn

e

k

ro

je

n

o

rm

a

ln

e

W

n

a

je

m

n

e

p

rn

e

k

ro

je

n

o

rm

a

ln

e

i

li

n

ia

g

e

o

d

e

n

y

jn

a

i

li

n

ia

g

e

o

d

e

n

y

jn

a

2

⋅1

0

-8

m

9

⋅1

0

-1

0

m

2

⋅1

0

-1

1

m

s´

-

s

0

.1

1

2

”

0

.0

2

8

”

0

.0

0

7

”

α´

1

-

α

1

2

0

0

k

m

1

0

0

k

m

5

0

k

m

s

=

...

2
sin

cos

12

1

1

2

2

2

2

1

1

+

=
−′

α

α

α

B

a

s

e

...

2

si

n

co

s

3

6

0

1

2

1

4

4

5

4

+

=

−′

α

B

a

s

e

s

s

(C

)

jw

(C

)

jw

2

8

2

8

/

3

2

/

3

2

T

r

T

r

ó

ó

jk

jk

ą

ą

ty

g

e

o

d

e

n

y

jn

e

i

i

c

h

ty

g

e

o

d

e

n

y

jn

e

i

i

c

h

ro

n

w

i

ro

n

w

i

ą

ą

n

y

w

a

n

ie

n

y

w

a

n

ie

T

ró

jk

ą

te

m

g

e

o

d

e

zy

jn

y

m

je

st

t

ró

jk

ą

t

n

a

p

o

w

ie

rz

ch

n

i

e

lip

so

id

y

o

b

ro

to

w

e

j

u

tw

o

rz

o

n

y

p

rz

e

z

tr

zy

ł

u

k

i

lin

ii

g

e

o

d

e

zy

jn

y

ch

.

R

o

zw

ią

za

n

ie

m

t

ró

jk

ą

ta

g

e

o

d

e

zy

jn

e

g

o

n

a

zy

w

a

m

y

o

b

lic

ze

n

ie

j

e

g

o

e

le

m

e

n

tó

w

n

a

p

o

d

st

a

w

ie

t

rz

e

ch

zn

a

n

y

ch

e

le

m

e

n

tó

w

,

w

t

y

m

p

rz

y

n

a

jm

n

ie

j

je

d

n

e

g

o

b

o

k

u

i

z

n

a

n

e

g

o

j

e

g

o

p

o

ło

ż

e

n

ia

n

a

e

lip

so

id

zi

e

.

M

a

łe

t

ró

jk

ą

ty

o

b

o

k

a

ch

d

o

9

0

k

m

m

o

ż

n

a

r

o

zw

ią

zy

w

a

ć

n

a

s

fe

rz

e

o

p

ro

m

ie

n

iu

r

ó

w

n

y

m

ś

re

d

n

ie

m

u

p

ro

m

ie

n

io

w

i

k

rz

y

w

iz

n

y

o

b

lic

zo

n

e

m

u

d

la

ś

re

d

n

ie

j

a

ry

tm

e

ty

cz

n

e

j

sz

e

ro

k

o

ś

ci

z

w

ie

rz

ch

o

łk

ó

w

t

ró

jk

ą

ta

R

o

zw

ią

zy

w

a

n

ie

t

ró

jk

ą

tó

w

g

e

o

d

e

zy

jn

y

ch

m

ia

ło

z

n

a

cz

e

n

ie

w

s

ie

ci

a

ch

tr

ia

n

g

u

la

cy

jn

y

ch

,

g

d

zi

e

d

la

o

b

lic

ze

n

ia

w

sp

ó

łr

zę

d

n

y

ch

n

a

jp

ie

rw

n

a

le

ż

a

ło

zn

a

le

źć

w

sz

y

st

k

ie

b

o

k

i

w

t

ró

jk

ą

ta

ch

..

.

(C

)

jw

(C

)

jw

2

9

2

9

/

3

2

/

3

2

N

a

d

m

ia

r

N

a

d

m

ia

r

((

k

(

(

(

(

)

((

k

(

(

(

(

)

s

fe

ry

c

n

n

y

s

fe

ry

c

n

n

y

ε

=

P

R

∆ 2

g

d

zi

e

P

∆

o

zn

a

cz

a

p

o

le

t

ró

jk

ą

ta

,

k

tó

re

m

o

ż

n

a

w

y

zn

a

cz

y

ć

ja

k

o

p

o

le

tr

ó

jk

ą

ta

p

ła

sk

ie

g

o

n

p

.:

2

1

2

si

n

R

A

c

b

=

ε

R

to

p

ro

m

ie

ń

sf

e

ry

,

n

a

k

tó

re

j

p

o

ło

ż

o

n

y

j

e

st

t

ró

jk

ą

t

(C

)

jw

(C

)

jw

3

0

3

0

/

3

2

/

3

2

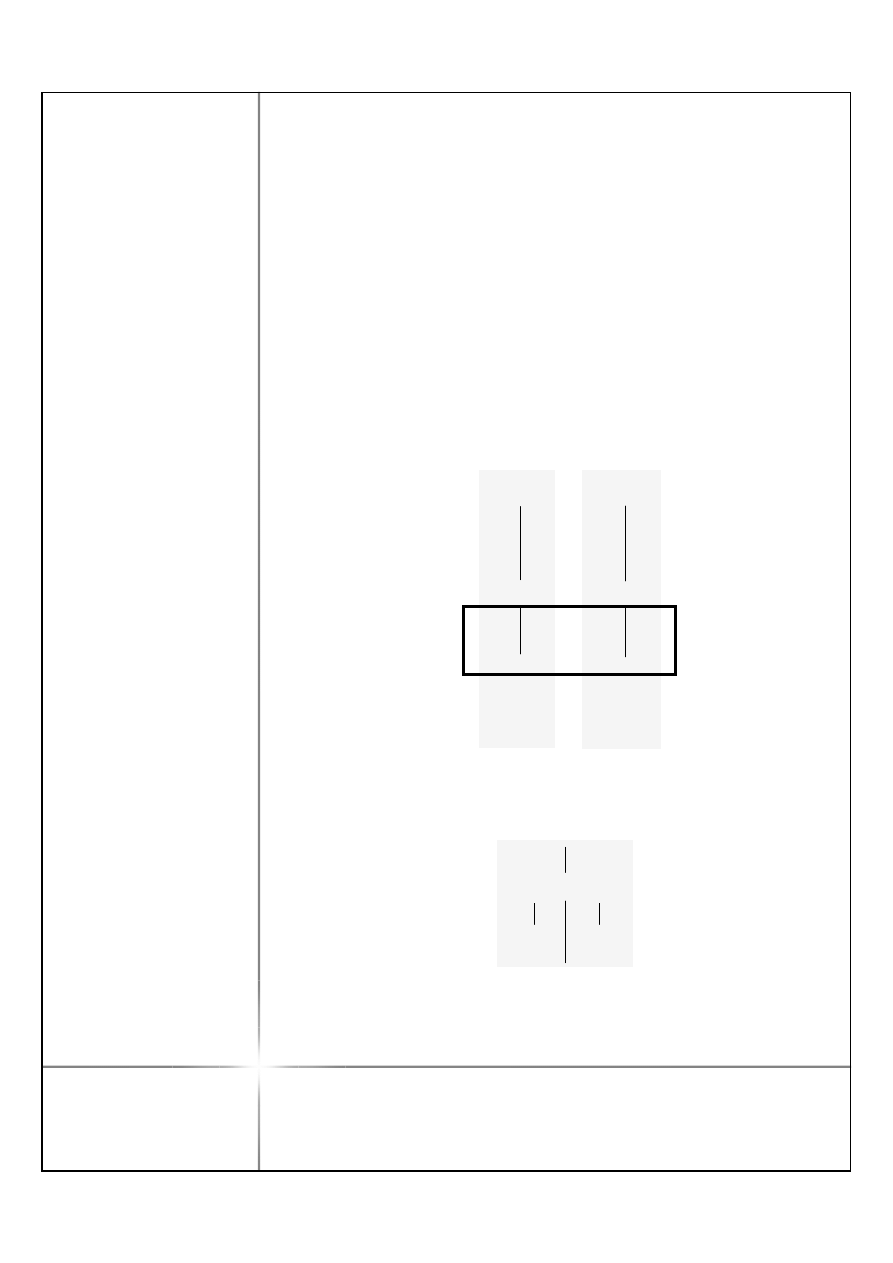
Me

to

d

a

Me

to

d

a

L

e

g

e

n

d

re

L

e

g

e

n

d

re

’

’

a

a

T

w

ie

rd

ze

n

ie

L

e

g

e

n

d

re

’a

m

ó

w

i,

ż

e

m

a

ły

t

ró

jk

ą

t

sf

e

ry

cz

n

y

m

o

ż

n

a

ro

zw

ią

za

ć

za

m

ie

n

ia

ją

c

g

o

n

a

t

ró

jk

ą

t

p

ła

sk

i,

w

k

tó

ry

ch

b

o

k

i

p

o

zo

st

a

ją

ró

w

n

e

t

y

m

n

a

s

fe

rz

e

,

a

k

a

ż

d

y

k

ą

t

je

st

z

m

n

ie

js

zo

n

y

o

1

/3

n

a

d

m

ia

ru

sf

e

ry

cz

n

e

g

o

D

la

t

ró

jk

ą

tó

w

o

b

o

k

a

ch

w

ię

k

sz

y

ch

o

d

9

0

k

m

s

to

su

je

s

ię

tz

w

.

ro

zs

ze

rz

o

n

e

t

w

ie

rd

ze

n

ie

L

e

g

e

n

d

re

’a

,

w

k

tó

ry

m

u

w

zg

lę

d

n

ia

s

ię

ró

ż

n

ic

ę

p

o

m

ię

d

zy

p

o

le

m

t

ró

jk

ą

ta

p

ła

sk

ie

g

o

i

s

fe

ry

cz

n

e

g

o

ε

ε

1

2

2

2

2

2

2

1

8

3

=

+













=

+

+

m

R

m

a

b

c

,

.

(C

)

jw

(C

)

jw

3

1

3

1

/

3

2

/

3

2

Me

to

d

a

a

d

d

it

a

m

e

n

t

Me

to

d

a

a

d

d

it

a

m

e

n

t

ó

ó

w

w

(

(

S

o

ld

n

d

ra

S

o

ld

n

d

ra

)

)

Z

Z

m

iZ

Z

Z

t

ró

jką

tZ

(f

(

ry(tZ

(

g

o

Z

Z

t

ró

jką

t

p

łZ

(ki

w

t

(

j

m

(

to

d

ti

(

p

o

l(

g

Z

Z

Z

p

o

to

(t

Z

w

i(

Z

iu

d

w

ó

(h

ką

tó

w

(f

(

ry(tZ

y(h

Z

i(

tm

i(

Z

io

Z

y(h

,

tZ

ś

b

o

ki

tr

ó

jką

tZ

p

łZ

(ki

(

g

o

u

ty

(ku

j(

(i

ę

p

o

p

rt

(

t

d

o

d

Z

Z

i(

d

o

b

o

kó

w

t

ró

jką

tZ

(f

(

ry(tZ

(

g

o

t

t

w

.

a

d

d

it

a

m

e

n

tó

w

l

in

io

w

ych

Z

lb

o

i

Z

Z

(

t(

j

a

lg

e

b

ra

icz

n

ych

1

1

sin

sin

b

a

R

b

R

a

=

...

1

2

0

6

4

5

2

3

1

+

+

−
=

R

a

R

a

a

a

...

1

2

0

6

4

5

2

3

1

+

+

−
=

R

b

R

b

b

b

W

sp

ó

łc

ze

ś

n

ie

r

za

d

k

o

r

o

zw

ią

zu

je

s

ię

tr

ó

jk

ą

ty

,

a

j

e

ś

li

ju

ż

to

w

y

k

o

rz

y

st

u

ją

c

w

p

ro

st

(

b

e

z

u

p

ro

sz

cz

e

ń

)

w

zo

ry

tr

y

g

o

n

o

m

e

tr

ii

sf

e

ry

cz

n

e

j

n

p

.

w

zó

r

si

n

u

so

w

y

(C

)

jw

(C

)

jw

3

2

3

2

/

3

2

/

3

2

R

o

n

w

i

R

o

n

w

i

ą

ą

n

a

n

ie

t

r

n

a

n

ie

t

r

ó

ó

jk

jk

ą

ą

ta

ta

K

o

le

jn

o

ś

ć

ro

zw

ią

za

n

ia

:

1

.

O

b

lic

ze

n

ie

n

a

d

m

ia

ru

s

fe

ry

cz

n

e

g

o

2

.

W

y

ró

w

n

a

n

ie

k

ą

tó

w

w

t

ró

jk

ą

ci

e

s

fe

ry

cz

n

y

m

A

+

B

+

C

=

1

8

0

o

+

ε

+

ω

3

.

R

o

zw

ią

za

n

ie

t

ró

jk

ą

ta

d

o

w

o

ln

ą

z

m

e

to

d