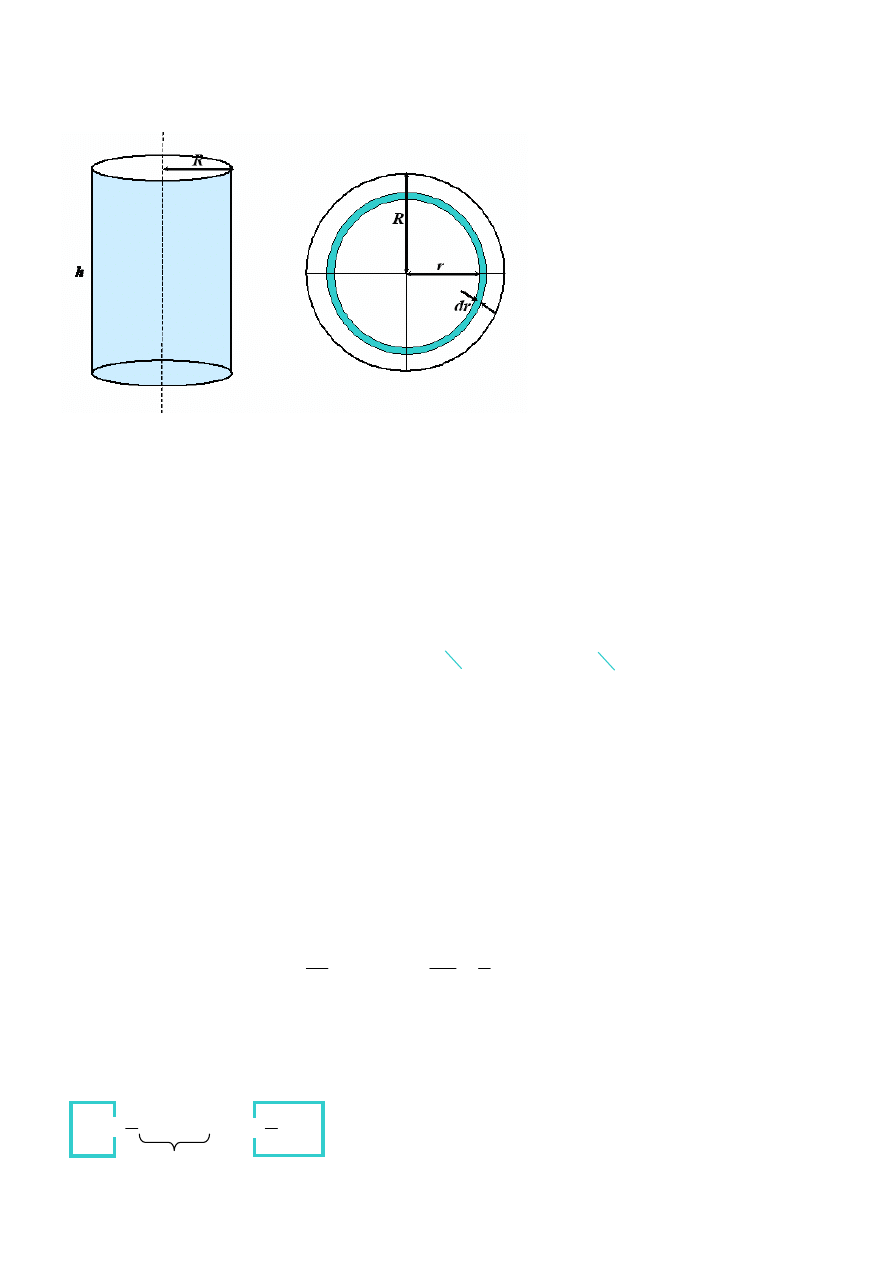
Obliczenie momentu bezwładności jednorodnego walca względem osi
symetrii

widok z boku

widok z góry

z definicji momentu bezwładności dla ciała o ciągłym rozkładzie masy

∫

=

m

w

dm

r

I

2

0

(1)

(indeks „0” oznacza moment bezwładności względem osi przechodzącej przez środek masy)
jako element dm wybieramy powłokę cylindryczną o promieniu wewnętrznym r i grubości
dr

→

0

dV

dm

ρ

=

dr

r

h

r

dr

dr

r

r

h

h

r

h

dr

r

V

V

dV

r

dr

r

π

π

π

π

2

)

2

(

)

(

2

2

2

2

2

=

−

+

+

=

−

+

=

−

=

+

dr

r

h

dm

π

ρ 2

⋅

=

(2)

dm zostało wyrażone w funkcji r i dr; zmiana zmiennej całkowania pociąga za sobą
konieczność zmiany granic całkowania

∫

∫

→

R

m

dr

dm

0

K

K

podstawiamy (2) do (1):

...

dr

r

h

r

dm

r

I

R

m

w

=

⋅

=

=

∫

∫

ρ

π

2

0

2

2

0

wielkości stałe wyciągamy przed znak całki

4

4

0

4

0

3

2

1

4

2

4

2

2

R

h

R

h

r

h

dr

r

h

...

R

R

ρ

π

ρ

π

ρ

π

ρ

π

=

=













=

=

∫

masa całkowita walca

h

R

V

m

2

π

ρ

ρ

⋅

=

=

stąd moment bezwładności

2

2

2

0

2

1

2

1

R

m

R

h

R

I

w

=

⋅

=

π

ρ

= m