Zadania z matematyki

Granice ciągów

1. Korzystając z definicji granicy ciągu wykazać, że:

1.1

lim

n

→∞

n + 2

2n

− 1

=

1

2

,

1.2

lim

n

→∞

2n

2

+ 3n + 1

n

2

+ n + 1

= 2,

1.3

lim

n

→∞

n

3

n

= 0,

1.4

lim

n

→∞

(

−1)

n

̸= 0.

2. Znaleźć granice:

2.1

lim

n

→∞

(n + 1)

2

2n

2

,

2.2

lim

n

→∞

(n + 1)

3

− (n − 1)

3

(n + 1)

2

+ (n

− 1)

2

,

2.3

lim

n

→∞

(

√

n

2

+ 1 + n)

2

3

√

n

6

+ 1

,

2.4

lim

n

→∞

4

√

n

5

+ 2

−

3

√

n

2

+ 1

5

√

n

4

+ 2

−

2

√

n

3

+ 1

,

2.5

lim

n

→∞

n!

(n + 1)!

− n!

,

2.6

lim

n

→∞

1

n

2

(1 + 2 + . . . + n),

2.7

lim

n

→∞

(

1

− 2 + 3 − 4 + . . . − 2n

√

n

2

+ 1

)

,

2.8

lim

n

→∞

(

1

1

· 2

+

1

2

· 3

+ . . . +

1

(n

− 1) · n

)

,

2.9

lim

n

→∞

2

n

− 1

2

n

+ 1

,

2.10 lim

n

→∞

2

1

n

− 1

2

1

n

+ 1

,

2.11 lim

n

→∞

n

√

2

n

+ 3

n

,

2.12 lim

n

→∞

n

√

3

n

− 2

n

,

2.13 lim

n

→∞

n

√

n + 2

n

,

2.14 lim

n

→∞

n

100

2

n

,

2.15 lim

n

→∞

n

√

10

n

+ 9

n

+ 7

n

,

2.16 lim

n

→∞

n

√

5

n

− 3

n

+ 2

n

,

2.16 lim

n

→∞

n

√

3n

4

+ 2n

2

+ 1,

2.17 lim

n

→∞

n

√

2n

3

− 3n

2

+ 15,

1

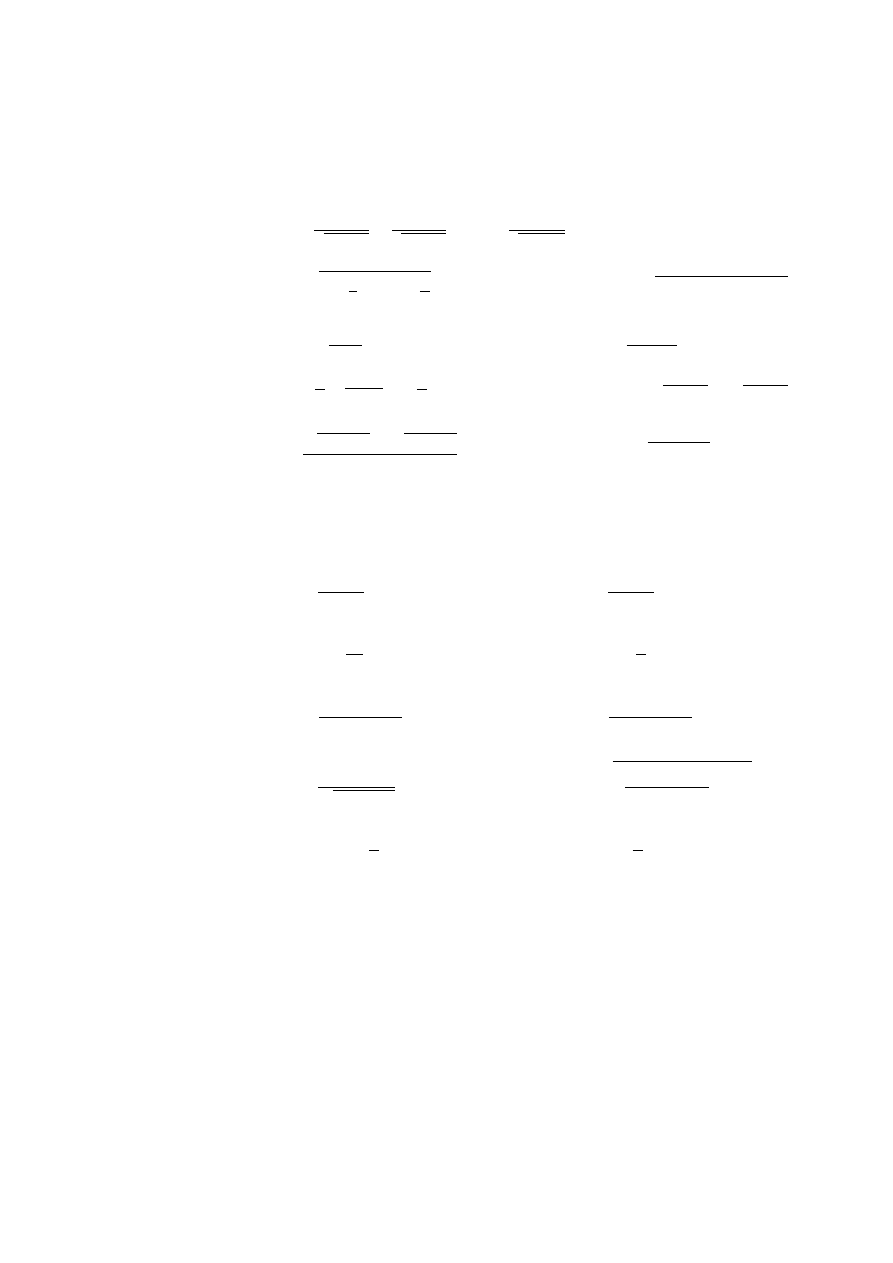
2.18 lim

n

→∞

(

1

√

n

2

+ 1

+

1

√

n

2

+ 2

+ . . . +

1

√

n

2

+ n

)

,

2.19 lim

n

→∞

n

√

1 +

1

2

+ . . . +

1

n

,

2.20 lim

n

→∞

n2

√

(n + 1)(n + 2)...2n,

2.21 lim lim

n

→∞

sin n

n

,

2.22 lim

x

→1

n sin n!

(n + 1)

,

2.23 lim

n

→∞

√

n(

√

n + 3

−

√

n),

2.24 lim

n

→∞

n(

√

n

2

+ 1

−

√

n

2

− 1),

2.25 lim

n

→∞

√

1 + 2n

2

−

√

4n

2

− 1

n

,

2.26 lim

n

→∞

3

√

n

3

+ 4n

2

− n.

3. Wyznaczyć granice ciągów:

3.1

x

n

=

(

2n + 1

2n

− 2

)

n

,

3.2

x

n

=

(

3n

− 1

3n + 1

)

2n

−1

,

3.3

x

n

=

(

1 +

1

n

2

)

n

)

2n+3

,

3.4

x

n

=

(

1 +

1

n

)

n

2

,

3.5

x

n

=

(

n

2

+ 7n + 3

n

2

+ 2n

− 1

)

2n+3

,

3.4

x

n

=

(

n

2

− 1

n

2

+ 2n + 3

)

3n

−1

,

3.6

x

n

=

(

n

3

√

n

3

+ 2n

2

)

n

,

3.7

x

n

=

n

√(

n

2

+ 3n + 1

n

2

+ 5n + 1

)

n

2

+1

,

3.8

x

n

=

(

1 + sin

1

n

)

2n+1

,

3.8

x

n

=

(

cos

π

n

)

n

2

.

2